Árvores de decisão e arquitetura de modelo
Quando o assunto é arquitetura, é comum pensar em edifícios. A arquitetura é responsável pela forma como um prédio é estruturado: a altura, a profundidade, o número de andares e como os elementos se conectam internamente. Ela também determina como o prédio é usado: onde é a entrada e a saída dele.
Em machine learning, a arquitetura refere-se a um conceito semelhante. Quantos parâmetros ele tem e como eles estão vinculados para obter um cálculo? É preciso realizar muitos cálculos em paralelo (largura) ou há operações seriais que contam com um cálculo anterior (profundidade)? Como podemos fornecer entradas para esse modelo e como podemos receber saídas? Essas decisões de arquitetura normalmente se aplicam apenas aos modelos mais complexos, e as decisões de arquitetura podem variar de simples a complexas. Essas decisões costumam ser tomadas antes que o modelo seja treinado, embora, em algumas circunstâncias, haja espaço para fazer alterações após o treinamento.
Vamos explorar isso mais concretamente com as árvores de decisão como exemplo.
O que é uma árvore de decisão?
Em essência, uma árvore de decisão é um fluxograma. As árvores de decisão são um modelo de categorização que divide as decisões em várias etapas.
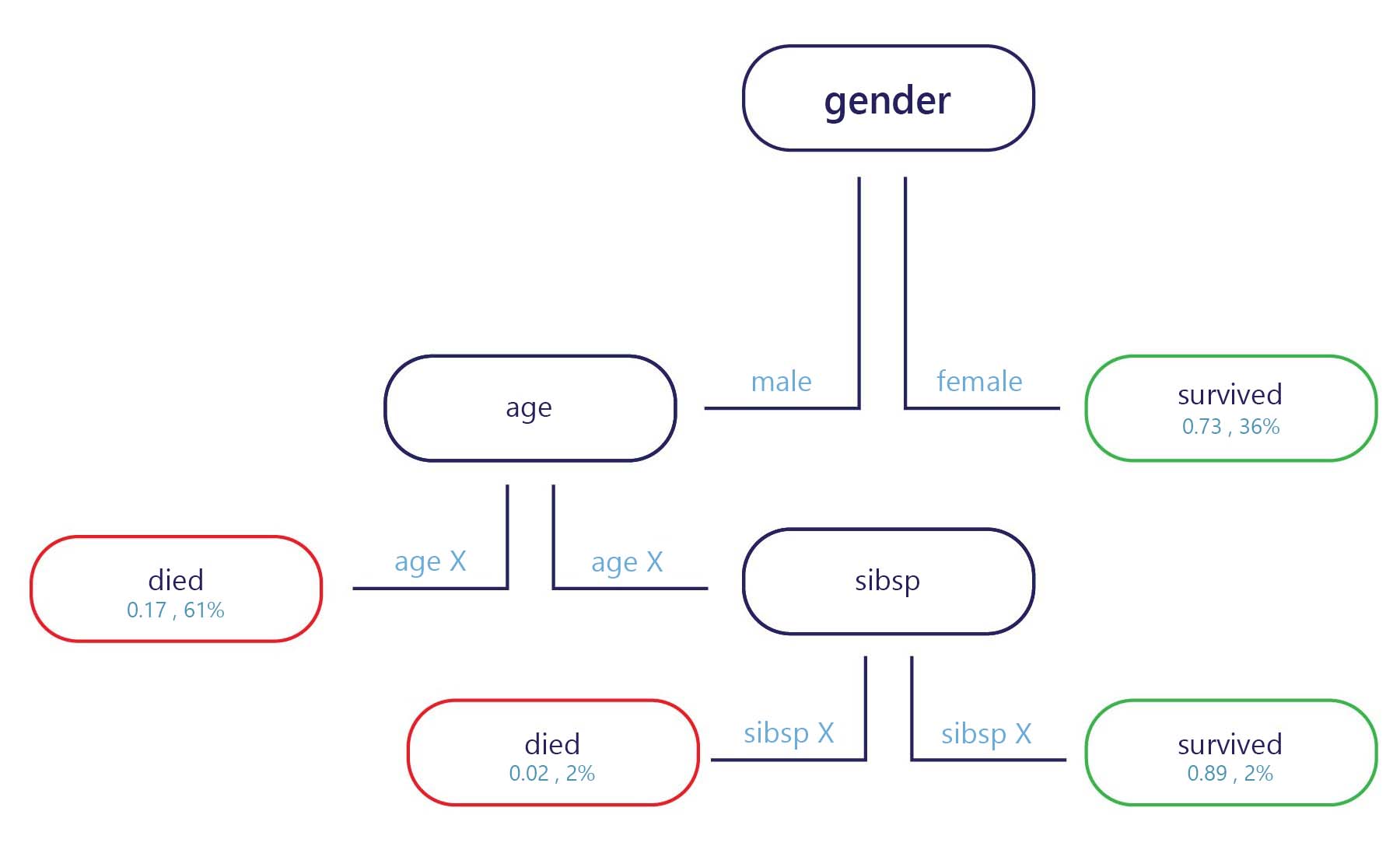
O exemplo, se fornecido no ponto de entrada (parte superior do diagrama acima), e cada ponto de saída tem um rótulo (parte inferior do diagrama). Em cada nó, uma instrução if simples decide para qual branch o exemplo passa na sequência. Depois que a ramificação chegar ao final da árvore (as folhas), ela receberá um rótulo.
Como as árvores de decisão são treinadas?
As árvores de decisão são treinadas em um nó ou um ponto de decisão por vez. No primeiro nó, todo o conjunto de treinamento é avaliado. Depois disso, é selecionada uma característica que pode separar melhor o conjunto em dois subconjuntos com rótulos mais homogêneos. Por exemplo, imagine que nosso conjunto de treinamento seja o seguinte:
| Peso (característica) | Idade (característica) | Ganhou uma medalha (Rótulo) |
|---|---|---|
| 90 | 18 | Não |
| 80 | 20 | Não |
| 70 | 19 | Não |
| 70 | 25 | Não |
| 60 | 18 | Sim |
| 80 | 28 | Sim |
| 85 | 26 | Sim |
| 90 | 25 | Sim |
Em busca de uma regra que divida esses dados da melhor maneira, é possível dividi-los por idade, em cerca de 24 anos, porque a maioria dos atletas que ganharam medalhas tinha mais de 24 anos. Essa divisão nos dará dois subconjuntos de dados.
Subconjunto 1
| Peso (característica) | Idade (característica) | Ganhou uma medalha (Rótulo) |
|---|---|---|
| 90 | 18 | Não |
| 80 | 20 | Não |
| 70 | 19 | Não |
| 60 | 18 | Sim |
Subconjunto 2
| Peso (característica) | Idade (característica) | Ganhou uma medalha (Rótulo) |
|---|---|---|
| 70 | 25 | Não |
| 80 | 28 | Sim |
| 85 | 26 | Sim |
| 90 | 25 | Sim |
Ao parar aqui, você tem um modelo simples com um nó e duas folhas. A folha 1 contém os atletas que não ganharam medalhas e tem 75% de precisão no conjunto de treinamento. A folha 2 contém os atletas que ganharam medalhas e também tem 75% de precisão no conjunto de treinamento.
No entanto, não precisamos parar aqui. Podemos continuar esse processo dividindo as folhas ainda mais.
No subconjunto 1, o primeiro novo nó pode ser dividido por peso, porque o único competidor que ganhou uma medalha tinha um peso menor do que as pessoas que não ganharam nenhuma. A regra pode ser definida como “peso < 65”. Há uma chance de pessoas com um peso < 65 terem ganho uma medalha, por isso, qualquer pessoa com peso ≥ 65 não atende a esse critério e pode ser previsto como alguém que não ganhou uma medalha.
No subconjunto 2, o segundo novo nó também pode ser dividido por peso, mas, desta vez, ele prevê que qualquer pessoa com um peso acima de 70 teria ganho uma medalha, excluindo todos abaixo desse peso.
Isso nos fornece uma árvore que poderá chegar a 100% de precisão no conjunto de treinamento.
Pontos fortes e fracos das árvores de decisão
As árvores de decisão são consideradas como tendo um baixo desvio. Em geral, isso significa que elas são boas para identificar características que são importantes para rotular algo corretamente.
O principal ponto fraco das árvores de decisão é o sobreajuste. Considere o exemplo fornecido acima: o modelo apresenta uma forma exata de calcular os atletas que têm a probabilidade de ganhar uma medalha, e isso preverá 100% do conjunto de dados de treinamento corretamente. Esse nível de precisão é incomum para modelos de machine learning, que normalmente cometem vários erros no conjunto de dados de treinamento. Um bom desempenho de treinamento não é algo ruim em si, mas a árvore se tornou tão especializada para o conjunto de treinamento que provavelmente não se sairá bem no conjunto de teste. Isso acontece porque a árvore conseguiu aprender relações no conjunto de treinamento que provavelmente não são reais, como o fato de um peso de 60 kg garantir uma medalha caso você tenha menos de 25 anos.
A arquitetura do modelo afeta o sobreajuste
O modo como estruturamos nossa árvore de decisão é fundamental para evitar os pontos fracos dela. Quanto mais profunda for a árvore, maior será a probabilidade de ela superajustar o conjunto de treinamento. Por exemplo, na árvore simples acima, se limitarmos a árvore apenas ao primeiro nó, ela cometerá erros no conjunto de treinamento, mas provavelmente se sairá melhor no conjunto de teste. Isso ocorre porque ela terá regras mais gerais sobre quem ganha a medalha, como “atletas acima de 24”, em vez de regras extremamente específicas que só podem se aplicar ao conjunto de treinamento.
Embora o foco aqui tenham sido as árvores, outros modelos complexos geralmente têm um ponto fraco semelhante que pode ser atenuado por meio de decisões sobre como estruturá-los ou como eles podem ser processados pelo treinamento.