Vetores one-hot
Até agora, cobrimos codificação de dados contínua (números de ponto flutuante), codificação de dados ordinais (geralmente números inteiros) e codificação de dados categóricos binários (sobreviveu/morreu, homem/mulher, etc.).
Agora vamos aprender como codificar dados e vamos explorar recursos de dados categóricos que tenham mais de duas classes. Também exploraremos os efeitos potencialmente prejudiciais de nossas decisões de melhoria de modelo sobre o desempenho do modelo.
Dados categóricos não são numéricos
Dados categóricos não funcionam com números da mesma forma que outros tipos de dados funcionam com números. Com os dados ordinais ou contínuos (numéricos), valores mais altos implicam um aumento no valor. Por exemplo, um preço de tíquete do Titanic de £30 é mais elevado do que um preço de tíquete de £12.
Por outro lado, os dados categóricos não têm ordem lógica. Teremos problemas se tentarmos codificar, como números, feições categóricas que tenham mais de duas classes.
Por exemplo, o Porto de Embarque tem três valores: C (Cherbourg), Q (Queenstown) e S (Southampton). Não podemos substituir esses símbolos por números. Se fizermos isso, implicaria que uma dessas portas é menor que os outras portas, enquanto outra é maior que as outras portas. Essa substituição não faz sentido.
Como exemplo desse problema, vamos tomar cuidado com o vento e modelar o relacionamento entre o Porto de Embarque e a Classe do Tíquete, tratando o Porto de Embarque como um número. Primeiro, definimos C < S < Q:
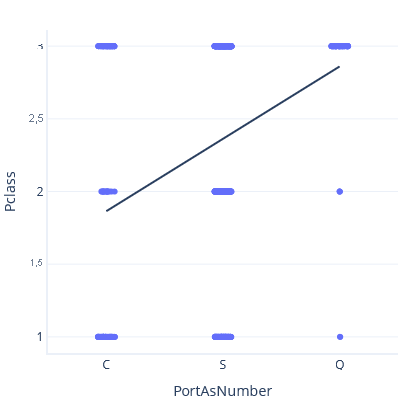
No gráfico, a linha prevê uma Classe de ~3 para o Porto Q.
Agora, configurando S < C < Q, obtemos uma linha de tendência e uma previsão completamente diferentes:
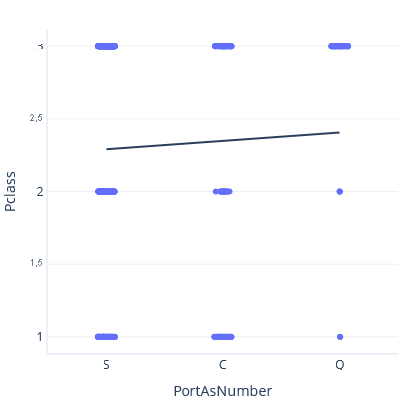
Nenhuma dessas linhas de tendência está correta. Não faz sentido tratar categorias como recursos contínuos. Então, como trabalhar com categorias?
Codificação one-hot
A codificação one-hot pode codificar dados categóricos de uma forma que evite esse problema. Cada categoria disponível obtém a própria coluna única, e uma determinada linha contém só um número de valor 1 na categoria à qual pertence.
Por exemplo, podemos codificar o valor da porta em três colunas: uma para Cherbourg, uma para Queenstown e uma para Southampton (a ordem exata aqui não tem relevância). Uma pessoa que embarcou em Cherbourg teria um número 1 na coluna Port_Cherbourg, como segue:
| Port_Cherbourg | Port_Queenstown | Port_Southampton |
|---|---|---|
| 1 | 0 | 0 |
Uma pessoa que embarcou em Queenstown teria um número 1 na segunda coluna:
| Port_Cherbourg | Port_Queenstown | Port_Southampton |
|---|---|---|
| 0 | 1 | 0 |
Uma pessoa que embarcou em Southampton teria um número 1 na terceira coluna
| Port_Cherbourg | Port_Queenstown | Port_Southampton |
|---|---|---|
| 0 | 0 | 1 |
Codificação one-hot, limpeza de dados e poder estatístico
Antes de usarmos a codificação one-hot, devemos entender que seu uso pode ter impactos positivos ou negativos no desempenho real de um modelo.
O que é o poder estatístico?
O poder estatístico refere-se à capacidade de um modelo de identificar de forma confiável relacionamentos reais entre recursos e rótulos. Por exemplo, um modelo com alto poder pode relatar uma relação entre o preço do ingresso e a taxa de sobrevivência, com alto grau de certeza. Por outro lado, um modelo com baixo poder estatístico pode relatar uma relação com baixo grau de certeza ou pode até mesmo não encontrar essa relação.
Vamos evitar a matemática aqui, mas lembre-se de que as escolhas que fazemos podem influenciar o poder dos nossos modelos.
Remover dados reduz o poder estatístico
Mencionamos várias vezes que a limpeza de dados, em parte, envolve a remoção de amostras de dados incompletas. Infelizmente, a limpeza de dados pode reduzir o poder estatístico. Por exemplo, vamos fingir que queremos prever a sobrevivência da viagem do Titanic com base nos seguintes dados:
| Preço do tíquete | Sobrevivência |
|---|---|
| £ 4 | 0 |
| £ 8 | 0 |
| £ 10 | 1 |
| £ 25 | 1 |
Poderíamos adivinhar que alguém com uma passagem no valor de £ 15 sobreviveria, porque todas as pessoas com passagens que custavam no mínimo £ 10 sobreviveram. Se tivéssemos menos dados, porém, essa suposição se tornaria mais difícil:
| Preço do tíquete | Sobrevivência |
|---|---|
| £ 4 | 0 |
| £ 8 | 0 |
| £ 25 | 1 |
Colunas sem valor reduzem o poder estatístico
Recursos que têm pouco valor também podem danificar o poder estatístico, especialmente quando o número de recursos (ou colunas) começa a se aproximar do número de amostras (ou linhas).
Por exemplo, digamos que queremos ser capazes de prever a sobrevivência com os seguintes dados:
| Preço do tíquete | Sobrevivência |
|---|---|
| £ 4 | 0 |
| £ 4 | 0 |
| £ 25 | 1 |
| £ 25 | 1 |
Poderíamos prever com confiança que alguém com uma passagem da Cabine A sobreviveria, porque todos com passagens de £25 sobreviveram.
No entanto, agora temos outro recurso (Cabine):
| Preço do tíquete | Cabine | Sobrevivência |
|---|---|---|
| £ 4 | Um | 0 |
| £ 4 | Um | 0 |
| £ 25 | B | 1 |
| £ 25 | B | 1 |
A cabine não fornece informações úteis, porque simplesmente corresponde ao preço do tíquete. Não está claro se alguém com uma passagem de £ 25 da cabine A sobreviveria. Eles perecem, como outros da cabine A, ou sobrevivem como aqueles com passagens de £ 25?
A codificação one-hot pode reduzir o poder estatístico
A codificação one-hot reduz o poder estatístico mais do que dados contínuos ou ordinais, porque requer várias colunas, uma para cada valor categórico possível. Por exemplo, se fizermos a codificação one-hot do porto de embarque, adicionaremos três entradas de modelo (C, S e Q).
Uma variável categórica se tornará útil se o número de categorias for substancialmente menor do que o número de amostras (linhas do conjunto de dados). Uma variável categórica também se tornará útil se fornecer informações que ainda não estão disponíveis para o modelo por meio de outras entradas.
Por exemplo, vimos que a probabilidade de sobrevivência era diferente para as pessoas que embarcaram em portos diferentes. Essa variação provavelmente reflete o fato de que a maioria das pessoas no porto de Queenstown tinha passagens de terceira classe. Portanto, o embarque provavelmente reduz um pouco o poder estatístico, sem acrescentar informações relevantes ao nosso modelo.
Por outro lado, a Cabine provavelmente tem uma forte influência na sobrevivência. Isso porque as cabines inferiores do navio se encheriam de água antes que as cabines mais próximas do convés superior do navio se enchessem de água. Dito isso, o conjunto de dados do Titanic contém 147 cabines diferentes. Isso reduz o poder estatístico do nosso modelo se os incluirmos. Talvez precisemos experimentar incluir ou excluir os dados Cabin em nosso modelo para ver se os dados Cabin podem nos ajudar.
Em nosso próximo exercício, finalmente construímos nosso modelo que prevê a sobrevivência da viagem do Titanic e praticaremos a codificação one-hot ao fazê-lo.