Aprendizado
O aprendizado profundo é uma forma avançada de aprendizado de máquina que tenta emular a maneira como o cérebro humano aprende. A chave para o aprendizado profundo é a criação de uma rede neural artificial que simula a atividade eletroquímica em neurônios biológicos utilizando funções matemáticas, como mostrado aqui.
| Rede Neural Biológica | Rede Neural Artificial |
|---|---|

|
|
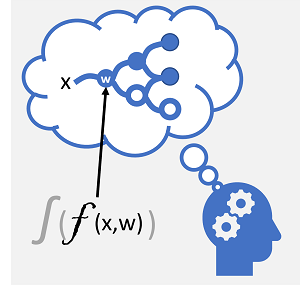
| Os neurônios disparam em resposta aos estímulos eletroquímicos. Quando disparado, o sinal é passado para os neurônios conectados. | Cada neurônio é uma função que opera em um valor de entrada (x) e um peso (w). A função é encapsulada em uma função de ativação que determina se a saída deve ser passada adiante. |
As redes neurais artificiais são compostas de várias camadas de neurônios - essencialmente definindo uma função profundamente aninhada. Essa arquitetura é o motivo pelo qual a técnica é chamada de aprendizado profundo e os modelos produzidos por ela são frequentemente chamados de redes neurais profundas (DNNs). Você pode utilizar redes neurais profundas para muitos tipos de problemas de aprendizado de máquina, incluindo regressão e classificação, bem como modelos mais especializados para processamento de linguagem natural e pesquisa visual computacional.
Assim como outras técnicas de aprendizado de máquina discutidas neste módulo, o aprendizado profundo envolve o ajuste dos dados de treinamento a uma função que pode prever um rótulo (y) com base no valor de um ou mais recursos (x). A função (f(x)) é a camada externa de uma função aninhada na qual cada camada da rede neural encapsula funções que operam em x e os valores de peso (w) associados a elas. O algoritmo utilizado para treinar o modelo envolve a alimentação iterativa dos valores dos recursos (x) nos dados de treinamento por meio das camadas para calcular as saídas para ŷ, validando o modelo para avaliar a distância entre os valores calculados ŷ e os valores conhecidos y (que quantifica o nível de erro, ou perda, no modelo) e, em seguida, modificando os pesos (w) para reduzir a perda. O modelo treinado inclui os valores finais de peso que resultam nas previsões mais precisas.
Exemplo: usando aprendizado profundo para classificação
Para entender melhor como um modelo de rede neural profunda funciona, vamos explorar um exemplo em que uma rede neural é utilizada para definir um modelo de classificação para espécies de pinguins.
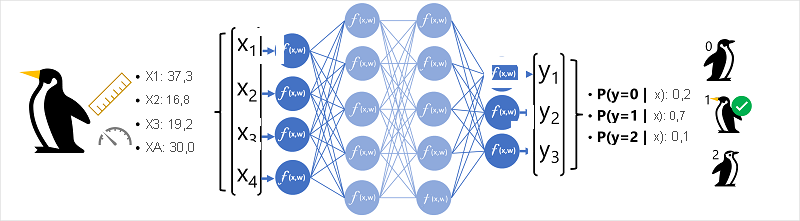
Os dados do recurso (x) consistem em algumas medidas de um pinguim. Especificamente, as medidas são:
- O comprimento do bico do pinguim.
- A profundidade do bico do pinguim.
- O comprimento das nadadeiras do pinguim.
- O peso do pinguim.
Nesse caso, x é um vetor de quatro valores, ou matematicamente, x=[x1,x2,x3,x4].
O rótulo que estamos tentando prever (y) é a espécie do pinguim, e que existem três espécies possíveis que será:
- Adélia
- Gentoo
- Chinstrap
Esse é um exemplo de um problema de classificação, no qual o modelo de machine learning deve prever a classe mais provável à qual uma observação pertence. Um modelo de classificação faz isso prevendo um rótulo que consiste na probabilidade de cada classe. Em outras palavras, y é um vetor de três valores de probabilidade; um para cada uma das classes possíveis: [P(y=0|x), P(y=1|x), P(y=2|x)].
O processo de inferência de uma classe de pinguins prevista utilizando essa rede é:
- O vetor de recursos para a observação de um pinguim é alimentado na camada de entrada da rede neural, que consiste em um neurônio para cada valor x. Neste exemplo, o seguinte vetor x é utilizado como entrada: [37.3, 16.8, 19.2, 30.0]
- Cada uma das funções da primeira camada de neurônios calcula uma soma ponderada, combinando o valor x e o peso w, e a passa para uma função de ativação que determina se ela atende ao limite que será passado para a próxima camada.
- Cada neurônio de uma camada está conectado a todos os neurônios da camada seguinte (uma arquitetura às vezes chamada de rede completamente conectada), de modo que os resultados de cada camada são alimentados pela rede até chegarem à camada de saída.
- A camada de saída produz um vetor de valores; nesse caso, utilizando uma função softmax ou similar para calcular a distribuição da probabilidade para as três classes possíveis de pinguins. Neste exemplo, o vetor de saída é: [0,2, 0,7, 0,1]
- Os elementos do vetor representam as probabilidades das classes 0, 1 e 2. O segundo valor é o mais alto, portanto o modelo prevê que a espécie do pinguim é 1 (Gentoo).
Como uma rede neural aprende?
Os pesos em uma rede neural são fundamentais para a forma como ela calcula os valores previstos para os rótulos. Durante o processo de treinamento, o modelo aprende os pesos que resultarão nas previsões mais precisas. Vamos explorar o processo de treinamento com um pouco mais de detalhes para entender como se dá esse aprendizado.
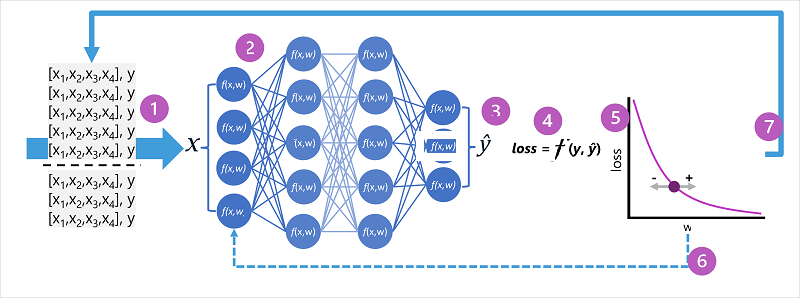
- Os conjuntos de dados de treinamento e validação são definidos e os recursos de treinamento alimentados na camada de entrada.
- Os neurônios em cada camada da rede aplicam seus pesos (que são inicialmente atribuídos de forma aleatória) e alimentam os dados por meio da rede.
- A camada de saída produz um vetor que contém os valores calculados para ŷ. Por exemplo, uma saída para uma previsão de classe de pinguim pode ser [0,3. 0,1. 0,6].
- Uma função de perda é utilizada para comparar os valores previstos ŷ com os valores conhecidos y e agregar a diferença (que é conhecida como perda). Por exemplo, se a classe conhecida para o caso que retornou a saída na etapa anterior for Chinstrap, então o valor y deverá ser [0.0, 0.0, 1.0]. A diferença absoluta entre isso e o vetor ŷ é [0,3, 0,1, 0,4]. Na realidade, a função de perda calcula a variação agregada de vários casos e a resume em um único valor de perda.
- Como a rede inteira é essencialmente uma grande função aninhada, uma função de otimização pode utilizar o cálculo diferencial para avaliar a influência de cada peso na rede sobre a perda e determinar como eles podem ser ajustados (para cima ou para baixo) para reduzir a quantidade de perda de modo geral. A técnica de otimização específica pode variar, mas geralmente envolve uma abordagem de descida de gradiente em que cada peso é aumentado ou diminuído para minimizar a perda.
- As alterações nos pesos são retropropagadas para as camadas da rede, substituindo os valores utilizados anteriormente.
- O processo é repetido em várias iterações (conhecidas como épocas) até que a perda seja minimizada e o modelo preveja com precisão aceitável.
Observação
Embora seja mais fácil pensar em cada caso dos dados de treinamento sendo passado pela rede um de cada vez, na realidade os dados são colocados em lote em matrizes e processados utilizando cálculos algébricos lineares. Por esse motivo, o treinamento da rede neural é melhor executado nos computadores com unidades de processamento gráfico (GPUs) otimizadas para a manipulação de vetores e matrizes.