Classificação multiclasse
A classificação multiclasse é utilizada para prever a qual das várias classes possíveis uma observação pertence. Como uma técnica de aprendizado de máquina supervisionada, ela segue o mesmo processo iterativo treinar, validar e avaliar que a regressão e a classificação binária, no qual um subconjunto dos dados de treinamento é retido para validar o modelo treinado.
Exemplo: classificação multiclasse
Os algoritmos de classificação multiclasse são utilizados para calcular valores de probabilidades para rótulos de várias classes, habilitando um modelo a prever a classe mais provável para uma determinada observação.
Vamos explorar um exemplo no qual temos algumas observações de pinguins, em que o comprimento da nadadeira (x) de cada pinguim é registrado. Para cada observação, os dados incluem a espécie do pinguim (y), que é codificada da seguinte forma:
- 0: Adélia
- 1: Gentoo
- 2: Chinstrap
Observação
Como nos exemplos anteriores deste módulo, um cenário real incluiria vários valores de recursos (x). Utilizaremos um único recurso para manter as coisas simples.
 |
 |
|---|---|
| Comprimento da nadadeira (x) | Espécie (y) |
| 167 | 0 |
| 172 | 0 |
| 225 | 2 |
| 197 | 1 |
| 189 | 1 |
| 232 | 2 |
| 158 | 0 |
Treinamento de um modelo de classificação multiclasse
Para treinar um modelo de classificação multiclasse, precisamos utilizar um algoritmo para ajustar os dados de treinamento a uma função que calcula um valor de probabilidade para cada classe possível. Existem dois tipos de algoritmo que você pode utilizar para fazer isso:
- Algoritmos One-vs-Rest (OvR)
- Algoritmos multinomiais
Algoritmos One-vs-Rest (OvR)
Os algoritmos One-vs-Rest treinam uma função de classificação binária para cada classe, cada uma calculando a probabilidade de que a observação seja um exemplo da classe de destino. Cada função calcula a probabilidade de a observação ser de uma classe específica em comparação com qualquer outra classe. Para o nosso modelo de classificação de espécies de pinguins, o algoritmo criaria essencialmente três funções de classificação binária:
- f0(x) = P(y=0 | x)
- f1(x) = P(y=1 | x)
- f2(x) = P(y=2 | x)
Cada algoritmo produz uma função sigmoide que calcula um valor de probabilidade entre 0,0 e 1,0. Um modelo treinado utilizando esse tipo de algoritmo prevê a classe para a função que produz a saída de maior probabilidade.
Algoritmos multinomiais
Uma abordagem alternativa é utilizar um algoritmo multinomial, que cria uma única função que retorna uma saída com vários valores. A saída é um vetor (uma matriz de valores) que contém a distribuição de probabilidades para todas as classes possíveis, com uma pontuação de probabilidade para cada classe que, quando totalizada, adiciona 1,0:
f(x) =[P(y=0|x), P(y=1|x), P(y=2|x)]
Um exemplo desse tipo de função é uma função softmax, que poderia produzir uma saída como a do exemplo a seguir:
[0.2, 0.3, 0.5]
Os elementos do vetor representam as probabilidades das classes 0, 1 e 2, respectivamente; portanto, nesse caso, a classe com a maior probabilidade é 2.
Independentemente do tipo de algoritmo utilizado, o modelo usa a função resultante para determinar a classe mais provável para um dado conjunto de recursos (x) e prevê o rótulo da classe correspondente (y).
Avaliação de um modelo de classificação multiclasse
Você pode avaliar um classificador multiclasse calculando as métricas de classificação binária para cada classe individual. Alternativamente, você pode calcular as métricas de agregação que levam em conta todas as classes.
Vamos supor que tenhamos validado nosso classificador multiclasse e obtido os seguintes resultados:
| Comprimento da nadadeira (x) | Espécies reais (y) | Espécies previstas (ŷ) |
|---|---|---|
| 165 | 0 | 0 |
| 171 | 0 | 0 |
| 205 | 2 | 1 |
| 195 | 1 | 1 |
| 183 | 1 | 1 |
| 221 | 2 | 2 |
| 214 | 2 | 2 |
A matriz de confusão de um classificador multiclasse é semelhante à de um classificador binário, exceto pelo fato de mostrar o número de previsões para cada combinação de rótulos de classe previsto (ŷ) e real (y):
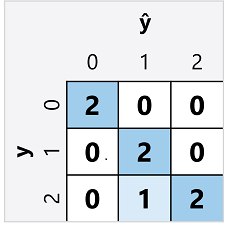
A partir dessa matriz de confusão, podemos determinar as métricas para cada classe individual da seguinte maneira:
| Classe | TP | TN | FP | FN | Exatidão | Recall | Precisão | Pontuação F1 |
|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 5 | 0 | 0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 1 | 2 | 4 | 1 | 0 | 0,86 | 1.0 | 0.67 | 0,8 |
| 2 | 2 | 4 | 0 | 1 | 0,86 | 0.67 | 1.0 | 0,8 |
Para calcular as métricas de exatidão geral, recall e precisão, você usa o total das métricas TP, TN, FP e FN:
- Exatidão geral = (13+6)÷(13+6+1+1) = 0,90
- Recordação geral = 6÷(6+1) = 0,86
- Precisão geral = 6÷(6+1) = 0,86
A pontuação F1 geral é calculada utilizando as métricas de recall e precisão gerais:
- Pontuação geral da F1 = (2x0,86x0,86)÷(0,86+0,86) = 0,86