O que é superposição em computação quântica?
Se o gato da unidade anterior fosse um gato quântico, o estado do gato quântico e do sistema de caixa seria o mesmo: a soma das seis posições diferentes do gato quântico em relação à caixa, ponderada pela probabilidade de encontrar o gato quântico nessa posição. A única diferença é que o gato clássico pode estar em uma (e apenas uma) das seis posições possíveis, enquanto o gato quântico pode estar em todas as seis posições ao mesmo tempo!
No mundo clássico, os objetos só podem estar em um estado por vez. No entanto, no mundo quântico, as partículas quânticas podem estar em vários estados ao mesmo tempo. Este fenômeno é chamado de superposição.
Na computação quântica, ninguém usa gatos quânticos - infelizmente - mas qubits. A palavra "qubit" significa "bit quântico". Assim como na computação clássica, em que a unidade básica de informações é o bit, na computação quântica, a unidade básica de informações é o qubit. E assim como o bit pode levar dois valores possíveis, 0 e 1, um qubit é qualquer partícula quântica que possa estar em dois estados possíveis. Por exemplo, um qubit pode ser um fóton, que pode ser polarizado em duas direções, ou um elétron, que pode estar em dois níveis de energia.
Como você pode representar a superposição em um qubit? Qual é a probabilidade de encontrar um qubit em um estado específico?
Como você pode representar a superposição em um qubit?
Um qubit é uma partícula quântica que tem duas posições ou estados possíveis. De maneira análoga ao bit clássico, os estados quânticos de um qubit também são denominados $0$ e $1$. Um qubit pode estar no estado $0$, no estado $1$ e em qualquer superposição desses dois estados. Como você pode representar essa superposição?
Imagine que você desenha um círculo e um eixo vertical e horizontal de modo que o ponto médio seja o centro do círculo. O estado $0$ é colocado na parte mais alta do eixo vertical e o estado $1$ na parte mais baixa.
Como você poderia descrever essa representação? Você poderia dizer que o estado $0$ é uma seta — ou um vetor— apontando para cima e o estado $1$ é um vetor apontando para baixo. Portanto, um bit clássico seria um vetor apontando para cima ou para baixo, nunca em outra direção.
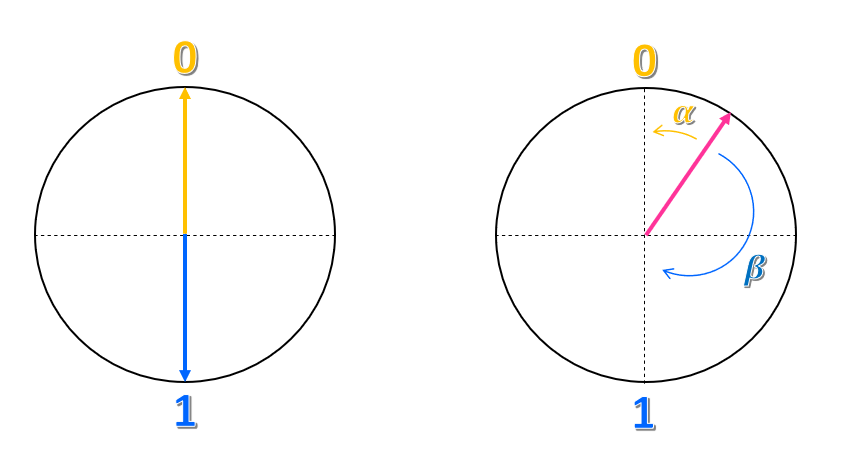
E quanto a qualquer outro ponto do círculo? Como você poderia representar esse estado? Assim como as coordenadas em um plano, você poderia tentar representá-lo como uma combinação entre os dois estados $0$ e $1$. Por exemplo, você poderia considerar a proximidade entre o vetor e o estado $0$ e denominar esse ângulo $\alpha$, e sua proximidade com o estado $1$ e denominar esse ângulo $\beta$. Poderíamos representar o estado como $\alpha 0 + \beta 1$. Assim, o estado é uma superposição dos estados $0$ e $1$.
Assim como o exemplo do gato e da caixa, o estado global de um qubit é a soma dos estados individuais, $0$ e $1$, ponderada pela probabilidade de o qubit se encontrar no estado em questão, $\alpha$ e $\beta$.
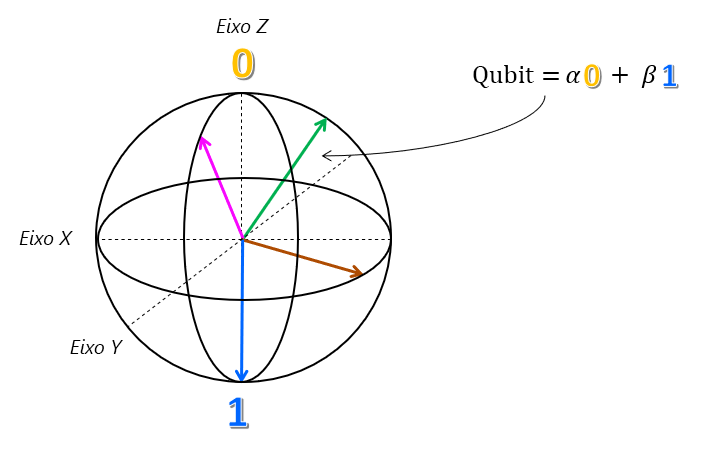
Essa representação de um qubit é realmente precisa e conhecida como a esfera de Bloch.
Dica
A esfera de Bloch é uma ferramenta poderosa, já que as operações que podemos executar em um qubit podem ser representadas como rotações sobre um dos eixos cardeais. Embora pensar em uma computação quântica como sequência de rotações seja uma ideia poderosa, é desafiador usar essa ideia para projetar e descrever algoritmos. O Q# alivia esse problema fornecendo uma linguagem para descrever essas rotações.
Qual é a probabilidade de encontrar um qubit em um estado?
Assim como o exemplo do gato e da caixa da unidade anterior, o estado global de um qubit é a soma dos estados individuais, $0$ e $1$, ponderada pela probabilidade de o qubit se encontrar no estado em questão, $\alpha$ e $\beta$. Os números $\alpha$ e $\beta$ representam o grau de "proximidade" entre o estado do qubit é e os estados $0$ e $1$, respectivamente. Então, $\alpha$ e $\beta$ representam a probabilidade de se encontrar o qubit no estado $0$ ou $1$? Não exatamente.
Os números $\alpha$ e $\beta$ são as amplitudes de probabilidade para cada estado. Seus valores absolutos — por exemplo, $|\alpha|^2$ — fornecem as probabilidades correspondentes. Por exemplo, a probabilidade de se observar o estado $0$ é $|\alpha|^2$, e a probabilidade de se observar o estado $1$ é $|\beta|^2$.
Os números $\alpha$ e $\beta$ podem ser números positivos, negativos ou até complexos. No entanto, em uma superposição quântica válida, a soma de todas as probabilidades deve ser igual a um: $|a|^2+|b|^2+|c|^1+|d|^2=1$. Essa restrição geralmente é conhecida como a condição de normalização. Você pode considerar a condição de normalização como o fato de sempre obter um resultado ao medir, de modo que a soma das probabilidades de medir cada resultado possível deve ser igual a um.