Como usar o emaranhamento para enviar informações?

Concluído

Nas unidades anteriores, você aprendeu que o emaranhamento quantum pode ser um excelente recurso para a comunicação quantum. Nesta unidade, você verá uma das mais famosas aplicações do entrelaçamento: o protocolo de teletransporte quântico.

No teletransporte, o emaranhamento é usado para transferir o estado de um qubit de um local para outro. O estado do qubit é transferido para outro qubit, mas o qubit em si não é movido fisicamente. Isso é uma coisa importante a ser lembrada! As informações do estado do qubit são transferidas para outro qubit que é usado como um recipiente para gravar as informações do qubit de mensagem.

O protocolo de teletransporte usa uma combinação de entrelaçamento e comunicação clássica. A comunicação clássica é importante porque o protocolo de teletransporte requer que o emissor comunique os resultados de suas medidas ao receptor. Isso significa que o teletransporte não pode enviar informações mais rápido do que a velocidade da luz. A comunicação clássica entre o emissor e o receptor é limitada pela velocidade da luz.

Vamos examinar o protocolo do teletransporte quântico.

O protocolo do teletransporte quântico

Alice e Bob trabalham juntos na mesma empresa. Alice trabalha em Seattle, e Bob em Los Angeles. Eles estão trabalhando em um projeto que exige que compartilhem informações quânticas. Eles decidem usar o teletransporte quântico para enviar informações quânticas entre eles.

Instalação inicial

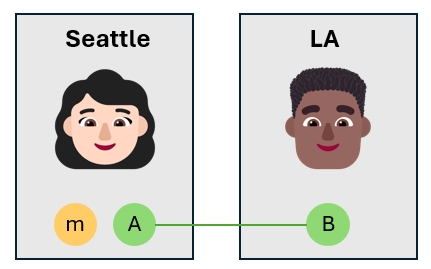
Alice e Bob têm um qubit cada que faz parte de um par emaranhado que foi preparado anteriormente. O par emaranhado é um estado de Bell, que é o estado

$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B} + \ket{1_A 1_B})$$

Alice tem um qubit extra – chamado de "qubit de mensagem" – e deseja enviar esse qubit para Bob. O qubit de mensagem está em um estado desconhecido que Alice quer teletransportar para Bob. O estado do qubit de mensagem é

$$\ket{m}=\alpha\ket{{0}_m + \beta\ket{{1}_m,$$

onde $\alpha$ e $\beta$ são números complexos.

O estado global dos qubits de Alice e Carlos é

$$\ket{\text{Global}}= (\alpha\ket{{0}_m + \beta\ket{1}_m) \otimes\frac1{\sqrt2}(\ket{0_A 0_B}+ \ket{1_A 1_B}) $$

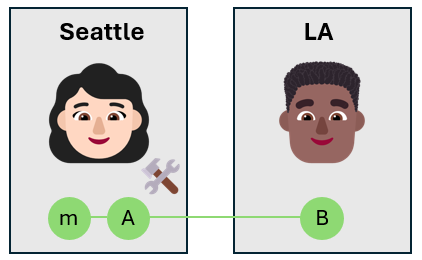
Alice emaranha o qubit de mensagem com seu próprio qubit

Alice pega o qubit de mensagem e o emaranha com seu próprio qubit $A$ usando um portão CNOT. O qubit de mensagem é o qubit de controle e o qubit de Alice é o qubit target. Isso cria um estado emaranhado de três qubits.

O qubit de mensagem está no estado desconhecido $\alpha\ket{0}_m + \beta\ket{1}_m$, portanto, depois de aplicar o portão CNOT, os qubits de Alice estão em uma superposição dos quatro estados de Bell. O estado global dos três qubits é

$$\ket{\text{Global}}=\frac1{{2}\ket{\phi^+}_\text{mA} (\alpha\ket{{0}_B + \beta\ket{{1}_B) + $$

$$ + \frac1{{2}\ket{\phi^-}_\text{mA} (\alpha\ket{0}_B - \beta\ket{1}_B) +$$

$$ + \frac1{{2}\ket{\psi^+}_\text{mA}(\alpha\ket{1}_B + \beta\ket{0}_B) + $$

$$ + \frac1{{2}\ket{\psi^-}_\text{mA} (\alpha\ket{1}_B- \beta\ket{0}_B)$$

O estado global dos qubits de Alice e Bob é uma superposição de quatro estados possíveis.

Dica

Um bom exercício é verificar se o estado global dos três qubits é o indicado acima. Você pode fazer isso aplicando a porta CNOT ao qubit de mensagem e ao qubit de Alice e expandindo o estado dos três qubits.

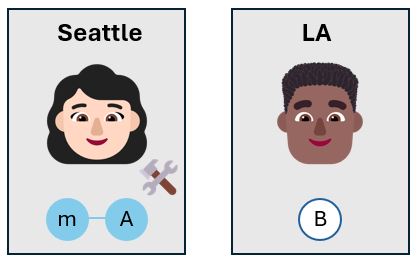
Alice mede os qubits

Alice então mede o qubit de mensagem e seu próprio qubit. Ela não mede os qubits na $base Z$como de costume, mas ela escolhe a base de Bell. A base de Bell consiste nos quatro estados de Bell, $\lbrace \ket{\phi^+}, \ket{\phi^-}, \ket{\psi^+, ^+}, \ket{\psi^-} \rbrace$.

Medindo o qubit de mensagem e seu próprio qubit na base de Bell, Alice projeta seus qubits em um dos quatro estados de Bell. Como os três qubits estão emaranhados, os resultados da medição estão correlacionados. Quando Alice mede seus qubits, o qubit de Bob também é projetado no estado correlacionado.

Por exemplo, se Alice medir seus qubits e observar o estado $\ket{\phi^-}$, o qubit de Bob será projetado no estado $\alpha\ket{0}_B - \beta\ket{1}_B$.

Alice liga para Bob

Alice liga para Bob e conta os resultados de suas medições. Ela usa um canal de comunicação clássica, como um telefonema ou uma mensagem de texto.

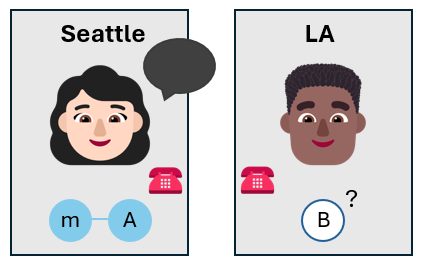
Bob agora sabe o estado do seu próprio qubit, sem ter que medi-lo. O estado do qubit de Bob pode não ser o mesmo que o estado do qubit de mensagem que Alice queria teletransportar, mas é próximo dele.

Bob aplica uma operação quântica

Em seguida, Bob pode recuperar o estado original do qubit de mensagem aplicando uma operação quântica específica ao seu qubit. A operação que Bob realiza depende do que Alice lhe disse ao telefone.

A operação que ele executa pode ser um portão Pauli $X$, um portão Pauli $Z$, ambos ou nenhum.

Por exemplo, se o resultado da medição de Alice for $\ket{\phi^-}$, Bob sabe que seu qubit está no estado $(\alpha\ket{0}_B - \beta\ket{1}_B)$. Ele só precisa aplicar um portão Pauli Z para recuperar o estado original do qubit de mensagem.

Alice mede	Bob aplica
$\ket{\phi^+}$	Nenhuma operação
$\ket{\phi^-}$	Portão Pauli Z
$\ket{\psi^+}$	Portão Pauli X
$\ket{\psi^-}$	Portão Pauli X seguido pelo portão Pauli Z

Esta operação final teletransporta efetivamente o estado do qubit de mensagem para o qubit de Bob. Missão cumprida!

Importante

Aplicar uma operação a um qubit não é o mesmo que medi-lo. Quando Bob aplica a operação, ele não mede seu qubit. Ele aplica uma operação quântica que altera o estado do qubit, mas não faz com que ele colapse.