Exercício: Criar o emaranhamento quântico com Q#
Na unidade anterior, você aprendeu sobre o conceito de emaranhamento quântico e estados de Bell.
Agora, vamos criar o emaranhamento quântico usando Q# e o Azure Quantum Development Kit. Para criar o emaranhamento, aplique duas operações quânticas: o portão do Hadamard e o portão do CNOT (Controlled-NOT).
A operação Controled-NOT (CNOT)
Quando dois qubits estão emaranhados, o estado de um qubit depende do estado do outro qubit. Portanto, para emaranhar dois qubits, você precisa de uma operação que afete ambos os qubits ao mesmo tempo. Isso é chamado de operação multiqubit.
Para criar o emaranhado quântico, você precisa da operação multiqubit CNOT, que significa Controlled-NOT. Essa operação usa dois qubits como entrada, um atua como qubit de controle e o outro é o qubit target. A operação CNOT inverte o estado do segundo qubit (o qubit target) se, e somente se, o estado do primeiro qubit (o qubit de controle) for $|1\rangle$.
| Entrada | Saída |
|---|---|
| $\ket{00}$ | $\ket{00}$ |
| $\ket{01}$ | $\ket{01}$ |
| $\ket{10}$ | $\ket{11}$ |
| $\ket{11}$ | $\ket{10}$ |
Em Q#, a operação CNOT atua em uma matriz de dois qubits e inverte o segundo qubit se o primeiro qubit for One.
Emaranhamento com uma operação CNOT
Aplicando a operação Hadamard, H e a operação Controlled-NOT, CNOT, você poderá transformar dois qubits no estado $|00\rangle$ para o estado de Bell $\ket{\phi^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.
Veja como ela funciona:
Pegue dois qubits no estado $|00\rangle$. O primeiro qubit é o qubit de controle e o segundo qubit é o qubit target.
Crie um estado de superposição somente no qubit de controle aplicando $H$.
$$H |0_c\rangle=\frac{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)$$
Dica
Os subscritos ${}_c$ e ${}_t$ especificam o controle e os qubits target.
Aplique o operador $CNOT$ ao qubit de controle, que está em um estado de superposição, e ao qubit target, que está no estado $|0_t\rangle$.
$$ CNOT \frac{1}{\sqrt{2}}(\ket{0_c}+\ket{1_c})\ket{0}_t = CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t}+|\ket{1_c 0_t})=$$$$=\frac{{1}{\sqrt2}(CNOT \ket{0_c 0_t} + CNOT \ket{1_c 0_t})=$$$$=\frac{1}{\sqrt2}(\ket{0_c 0_t}+\ket{1_c 1_t})$$
Criar um arquivo Q#
- Abra o Visual Studio Code.
- Selecione Arquivo > Novo Arquivo de Texto e salve-o como Main.qs.
- Select Exibir -> Paleta de Comandos e digite Q#: Definir o perfil target do QIR do Azure Quantum. Pressione Enter.
- Selecione Q#: Sem restrições.
Criar o estado de Bell $\ket{\phi^+}$
Vamos começar criando o estado de Bell $\ket{\phi^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.
Primeiro, importe o namespace
Microsoft.Quantum.Diagnosticsda biblioteca Standard, que contém a funçãoDumpMachine. Essa função mostra o estado atual dos qubits. Copie e cole o código Q# a seguir no arquivo Main.qs.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;Dica
Também é possível importar a biblioteca Standard substituindo
Microsoft.QuantumporStd. Por exemplo,import Std.Diagnostics.*é equivalente aimport Microsoft.Quantum.Diagnostics.*.Crie a operação
Mainque retorna dois valores de tipoResult, que são os resultados de medida dos qubits.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { // Your code goes here }Dentro da operação
Main, você aloca dois qubitsq1eq2, que serão emaranhados.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); }Aplique o portão do Hadamard,
H, ao primeiro qubit,q1, para colocá-lo em um estado de superposição. Em seguida, emaranhe os dois qubits usando a operaçãoCNOT.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); H(q1); CNOT(q1, q2); }Use a função
DumpMachinepara exibir o estado atual dos qubits. Isso não é o mesmo que medir os qubits.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); H(q1); CNOT(q1, q2); DumpMachine(); }Meça os qubits usando a operação
Me armazene os resultados emm1em2. Em seguida, use a operaçãoResetpara redefinir os qubits. Em Q#, você deverá sempre redefinir os qubits para o estado $|0\rangle$.import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); H(q1); CNOT(q1, q2); DumpMachine(); let (m1, m2) = (M(q1), M(q2)); Reset(q1); Reset(q2); }Por fim, retorne os resultados de medida dos qubits com a instrução
return. Seu arquivo Main.qs deve ter esta aparência:import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); H(q1); CNOT(q1, q2); DumpMachine(); let (m1, m2) = (M(q1), M(q2)); Reset(q1); Reset(q2); return (m1, m2); }Para executar seu programa no simulador interno, clique em Executar acima da operação
Mainou pressione Ctrl+F5. A saída será exibida no console de depuração.Os resultados da medição estão correlacionados, portanto, no final do programa, você obtém um resultado de
(Zero, Zero)ou(One, One)com igual probabilidade.Visualize o diagrama do circuito clicando em Circuito na lista de comandos acima da operação
Main. O diagrama do circuito mostra o portão Hadamard aplicado ao primeiro qubit e o portão CNOT aplicado a ambos os qubits.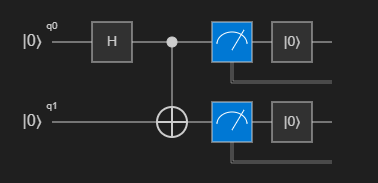
Crie outros estados de Bell
Para criar outros estados de Bell, você precisa aplicar operações adicionais de Pauli $X$ e $Z$ aos qubits.
Por exemplo, para criar o estado de Bell $\ket{\phi^-}=\frac1{\sqrt2}(|00\rangle-|11\rangle)$, você pode aplicar a operação Pauli $Z$ ao qubit de controle depois de aplicar o portão Hadamard. A operação$ Z$ inverte o estado de $\ket{+}$ para $\ket{-}$.
Dica
Os estados $\frac{{1}{\sqrt{2}}(|0\rangle+|1\rangle)$ e $\frac{1}{\sqrt{{2}}(|0\rangle -|1\rangle)$ também são conhecidos como $\ket{+}$ e $\ket{{-}$, respectivamente.
Veja como ela funciona:
Pegue dois qubits no estado $|00\rangle$.
Crie um estado de superposição somente no qubit de controle aplicando $H$.
$$H |0_c\rangle=\frac{{1}{\sqrt{2}}(|0_c\rangle+|1_c\rangle) =\ket{+}_c$$
Aplique a operação $Z$ ao qubit de controle.
$$Z \frac{{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)=\frac{1}{\sqrt{{2}}(|0_c\rangle-|1_c\rangle)=\ket{{-}_c$$
Aplique o operador $CNOT$ ao qubit de controle e ao qubit target, que está no estado $|0_t\rangle$.
$$ CNOT \frac{1}{\sqrt{2}}(\ket{0_c-1_c}\ket{})\ket{0}_t = CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t-1_c 0_t}}|\ket{){1}{\sqrt$$=\frac{=$$2}(CNOT \ket{0_c 0_t} - CNOT \ket{1_c 0_t})$$\frac{1}{\sqrt=$$=2}(\ket{0_c 0_t-1_c 1_t)}\ket{}$$
Da mesma forma, os estados de Bell $\ket{\psi^+}$ e $\ket{\psi^-}$ podem ser criados aplicando as operações Pauli $X$ e $Z$ aos qubits.
- O estado de Bell $\ket{\psi^+}=\frac1{\sqrt2}(|01\rangle+|10\rangle)$ pode ser criado aplicando a operação Pauli $X$ ao qubit target depois de aplicar o portão Hadamard.
- O estado de Bell $\ket{\psi^-}=\frac1{\sqrt2}(|01\rangle-|10\rangle)$ pode ser criado aplicando o Pauli $Z$ ao qubit de controle e o Pauli $X$ ao qubit target depois de aplicar o portão Hadamard.
Criar o estado de Bell $\ket{\phi^-}$ em Q#
Modifique o código Q# para criar o estado de Bell $\ket{\phi^-}$. Seu arquivo Main.qs deve ter esta aparência:
import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*; operation Main() : (Result, Result) { use (q1, q2) = (Qubit(), Qubit()); H(q1); Z(q1); // Apply the Pauli Z operation to the control qubit CNOT(q1, q2); DumpMachine(); let (m1, m2) = (M(q1), M(q2)); Reset(q1); Reset(q2); return (m1, m2); }Para executar seu programa no simulador interno, clique em Executar acima da operação
Mainou pressione Ctrl+F5. A saída será exibida no console de depuração.Visualize o diagrama do circuito clicando em Circuito na lista de comandos acima da operação
Main. O diagrama do circuito mostra o portão do Hadamard aplicado ao primeiro qubit, o portão do Pauli $Z$ aplicado ao primeiro qubit e a portão do CNOT aplicada a ambos os qubits.
Na próxima unidade, você aprenderá como usar o emaranhamento para teletransportar informações quânticas.