Aplicar técnicas avançadas de exploração de dados
As técnicas de exploração de dados avançadas, como análise de correlação e redução de dimensionalidade, ajudam a revelar relações e padrões ocultos nos dados, fornecendo insights valiosos que podem orientar a tomada de decisões.
Correlação
A correlação é um método estatístico usado para avaliar a força e a direção da relação linear entre duas variáveis quantitativas. O coeficiente de correlação varia de -1 a 1.
| Coeficiente de Correlação | Descrição |
|---|---|
| 1 | Indica uma correlação linear positiva perfeita. À medida que uma variável aumenta, a outra variável também aumenta. |
| -1 | Indica uma correlação linear negativa perfeita. À medida que uma variável aumenta, a outra variável diminui. |
| 0 | Indica que não existe nenhuma correlação linear. As duas variáveis não têm uma relação entre si. |
Vamos usar o conjunto de dados de pinguins para explicar como a correlação funciona.
Observação
O conjunto de dados de pinguins usado nesse exercício é um subconjunto dos dados coletados e disponibilizados pela Dra. Kristen Gorman e a Estação Palmer, Antártica LTER, membro da Rede de Pesquisa Ecológica de Longo Prazo.
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
# Load the penguins dataset
penguins = pd.read_csv('https://raw.githubusercontent.com/MicrosoftLearning/dp-data/main/penguins.csv')
# Calculate the correlation matrix
corr = penguins.corr()
# Create a heatmap
sns.heatmap(corr, annot=True)
plt.show()
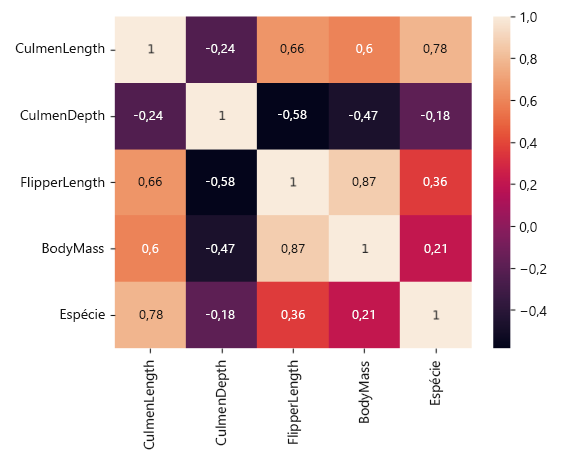
A correlação mais forte no conjunto de dados ocorre entre as variáveis FlipperLength e BodyMass, com um coeficiente de correlação de 0,87. Isso sugere que os pinguins com aletas maiores tendem a ter uma massa corporal maior.
A identificação e a análise de correlações são importantes pelos motivos a seguir.
- Análise preditiva: Se duas variáveis estiverem altamente correlacionadas, poderemos prever uma variável a partir da outra.
- Seleção de recursos: Se dois recursos estiverem altamente correlacionados, podemos descartar um, já que não fornece informações exclusivas.
- Como entender as relações: A correlação ajuda a entender a relação entre variáveis diferentes nos dados.
Importante
Fundamentalmente, a correlação não implica causalidade. Só porque duas variáveis estão correlacionadas isso não significa que as alterações em uma variável causem alterações na outra.
Análise de Componente Principal (ACP)
A Análise de Componente Principal (ACP) pode ser usada tanto para a exploração quanto para o pré-processamento de dados.
Em muitos cenários de dados do mundo real, lidamos com dados altamente dimensionais com os quais que pode ser difícil trabalhar. Quando usada para exploração, a ACP ajuda a reduzir o número de variáveis e, ao mesmo tempo, retém a maioria das informações originais. Isso faz com que os dados se tornem mais fáceis de trabalhar e tenham um uso menos intensivo de recursos com relação aos algoritmos de aprendizado de máquina.
Para simplificar o exemplo, estamos trabalhando com o conjunto de dados de pinguins que contém apenas cinco variáveis. No entanto, uma abordagem semelhante seria seguida se você trabalhasse com um conjunto de dados maior.
import pandas as pd
import seaborn as sns
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
# Load the penguins dataset
penguins = pd.read_csv('https://raw.githubusercontent.com/MicrosoftLearning/dp-data/main/penguins.csv')
# Remove missing values
penguins = penguins.dropna()
# Prepare the data and target
X = penguins.drop('Species', axis=1)
y = penguins['Species']
# Initialize and apply PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# Plot the data
plt.figure(figsize=(8, 6))
for color, target in zip(['navy', 'turquoise', 'darkorange'], penguins['Species'].unique()):
plt.scatter(X_pca[y == target, 0], X_pca[y == target, 1], color=color, alpha=.8, lw=2,
label=target)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('PCA of Penguins dataset')
plt.show()
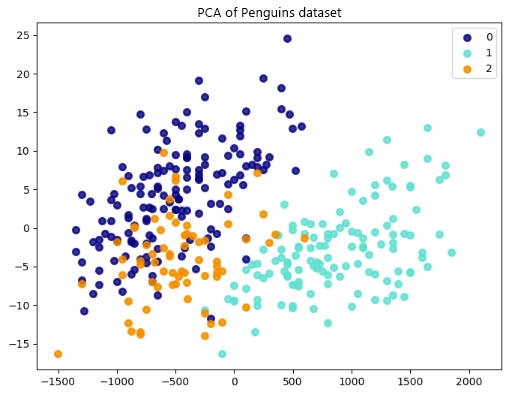
Ao aplicar a ACP no conjunto de dados de pinguins, podemos reduzir essas cinco variáveis a dois componentes principais que capturam a maior variação nos dados. Essa transformação reduz a dimensionalidade dos dados de cinco dimensões para duas. A seguir, poderemos criar um gráfico de dispersão 2D para visualizar os dados e identificar clusters de pinguins com características semelhantes.
Cada ponto no gráfico representa um pinguim do conjunto de dados. Os valores para o primeiro e o segundo componentes principais (x e y) determinam a posição de um ponto.
Essas são as novas variáveis que a ACP cria a partir de combinações lineares das variáveis CulmenLength, CulmenDepth, FlipperLength, BodyMass e Species. O primeiro componente principal captura a maior parte da variação nos dados e cada componente subsequente captura menos variação.
Os resultados mostram uma separação entre pinguins de diferentes espécies. Ou seja, pontos da mesma cor (espécies) estão mais próximos e pontos de cores diferentes estão mais distantes. As diferenças nas distribuições de recursos para classes diferentes resultam nessa separação, sugerindo que podemos distinguir essas espécies com base em seus atributos.