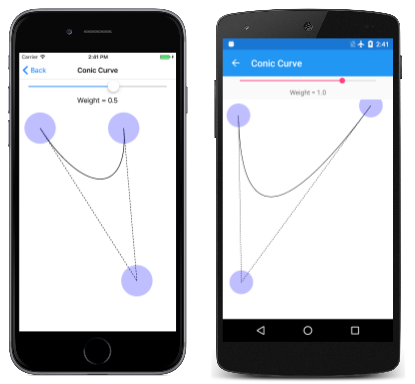
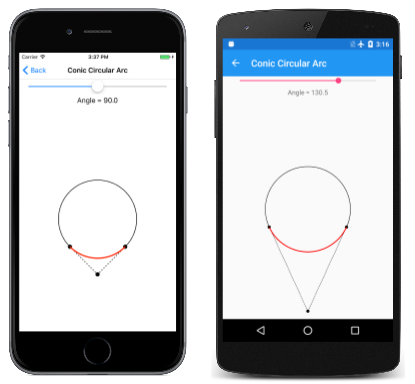
Três tipos de curvas de bézier
Explore como usar o SkiaSharp para renderizar curvas de Bézier cúbicas, quadráticas e cônicas
A curva de Bézier recebeu o nome de Pierre Bézier (1910 – 1999), engenheiro francês da montadora Renault, que usou a curva para o projeto assistido por computador de carrocerias.
As curvas de Bézier são conhecidas por serem bem adaptadas ao design interativo: são bem comportadas — em outras palavras, não há singularidades que façam com que a curva se torne infinita ou pesada — e geralmente são esteticamente agradáveis:

Os contornos de caracteres de fontes baseadas em computador são geralmente definidos com curvas de Bézier.
O artigo da Wikipédia sobre a curva de Bézier contém algumas informações de fundo úteis. O termo curva de Bézier na verdade se refere a uma família de curvas semelhantes. O SkiaSharp suporta três tipos de curvas de Bézier, chamadas de cúbicas, quadráticas e cônicas. O cônico também é conhecido como quadrático racional.
A curva cúbica de Bézier
O cúbico é o tipo de curva de Bézier que a maioria dos desenvolvedores pensa quando o assunto das curvas de Bézier vem à tona.
Você pode adicionar uma curva de Bézier cúbica a um SKPath objeto usando o CubicTo método com três SKPoint parâmetros ou a CubicTo sobrecarga com parâmetros e separados xy :
public void CubicTo (SKPoint point1, SKPoint point2, SKPoint point3)
public void CubicTo (Single x1, Single y1, Single x2, Single y2, Single x3, Single y3)
A curva começa no ponto atual do contorno. A curva cúbica completa de Bezier é definida por quatro pontos:
- ponto de partida: ponto atual no contorno, ou (0, 0) se
MoveTonão tiver sido chamado - Primeiro ponto de controle:
point1naCubicTochamada - Segundo ponto de controle:
point2naCubicTochamada - Ponto final:
point3naCubicTochamada
A curva resultante começa no ponto inicial e termina no ponto final. A curva geralmente não passa pelos dois pontos de controle; em vez disso, os pontos de controle funcionam como ímãs para puxar a curva em direção a eles.
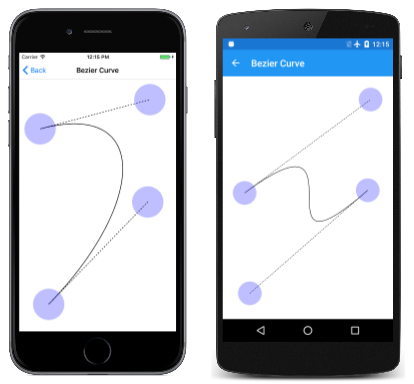
A melhor maneira de sentir a curva cúbica de Bézier é experimentando. Este é o propósito da página Curva de Bezier, que deriva de InteractivePage. O arquivo BezierCurvePage.xaml instancia o SKCanvasView e um TouchEffect. O arquivo code-behind BezierCurvePage.xaml.cs cria quatro TouchPoint objetos em seu construtor. O PaintSurface manipulador de eventos cria um SKPath para renderizar uma curva de Bézier com base nos quatro TouchPoint objetos e também desenha linhas tangentes pontilhadas dos pontos de controle para os pontos finais:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with cubic Bezier curve
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.CubicTo(touchPoints[1].Center,
touchPoints[2].Center,
touchPoints[3].Center);
canvas.DrawPath(path, strokePaint);
}
// Draw tangent lines
canvas.DrawLine(touchPoints[0].Center.X,
touchPoints[0].Center.Y,
touchPoints[1].Center.X,
touchPoints[1].Center.Y, dottedStrokePaint);
canvas.DrawLine(touchPoints[2].Center.X,
touchPoints[2].Center.Y,
touchPoints[3].Center.X,
touchPoints[3].Center.Y, dottedStrokePaint);
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
Aqui está em execução:
Matematicamente, a curva é um polinômio cúbico. A curva cruza uma reta em três pontos no máximo. No ponto inicial, a curva é sempre tangente e na mesma direção que uma linha reta do ponto inicial ao primeiro ponto de controle. No ponto final, a curva é sempre tangente e na mesma direção que uma linha reta do segundo ponto de controle até o ponto final.
A curva cúbica de Bézier é sempre delimitada por um quadrilátero convexo conectando os quatro pontos. Isso é chamado de casco convexo. Se os pontos de controle estiverem na linha reta entre o ponto inicial e o ponto final, a curva de Bézier será renderizada como uma linha reta. Mas a curva também pode se cruzar, como demonstra a terceira captura de tela.
Um contorno de caminho pode conter várias curvas cúbicas de Bézier conectadas, mas a conexão entre duas curvas cúbicas de Bézier será suave somente se os três pontos a seguir forem colineares (isto é, situarem-se em uma linha reta):
- o segundo ponto de controle da primeira curva
- o ponto final da primeira curva, que também é o ponto inicial da segunda curva
- o primeiro ponto de controle da segunda curva
No próximo artigo sobre SVG Path Data, você descobrirá uma facilidade para facilitar a definição de curvas de Bézier conectadas suaves.
Às vezes, é útil conhecer as equações paramétricas subjacentes que tornam uma curva cúbica de Bézier. Para t variando de 0 a 1, as equações paramétricas são as seguintes:
x(t) = (1 – t)³x₀ + 3t(1 – t)²x₁ + 3t²(1 – t)x₂ + t³x₃
y(t) = (1 – t)³y₀ + 3t(1 – t)²y₁ + 3t²(1 – t)y₂ + t³y₃
O expoente mais alto de 3 confirma que estes são polinômios cúbicos. É fácil verificar que quando t é igual a 0, o ponto é (x₀, y₀), que é o ponto de partida, e quando t é igual a 1, o ponto é (x₃, y₃), que é o ponto final. Perto do ponto inicial (para valores baixos de ), o primeiro ponto de tcontrole (x₁, y₁) tem um forte efeito, e perto do ponto final (valores altos de 't') o segundo ponto de controle (x₂, y₂) tem um forte efeito.
Aproximação da curva de Bezier a arcos circulares
Às vezes é conveniente usar uma curva de Bézier para renderizar um arco circular. Uma curva cúbica de Bézier pode aproximar um arco circular muito bem até um quarto de círculo, de modo que quatro curvas de Bézier conectadas podem definir um círculo inteiro. Essa aproximação é discutida em dois artigos publicados há mais de 25 anos:
Tor Dokken, et al, "Good Approximation of Circles by Curvature-Continuous Bézier curves", Computer Aided Geometric Design 7 (1990), 33-41.
Michael Goldapp, "Aproximação de Arcos Circulares por Polinômios Cúbicos", Computer Aided Geometric Design 8 (1991), 227-238.
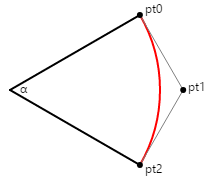
O diagrama a seguir mostra quatro pontos rotulados pto, pt1, pt2, e pt3 definindo uma curva de Bézier (mostrada em vermelho) que se aproxima de um arco circular:
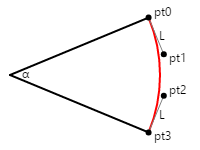
As linhas dos pontos inicial e final para os pontos de controle são tangente ao círculo e à curva de Bézier, e têm um comprimento de L. O primeiro artigo citado acima indica que a curva de Bézier se aproxima melhor de um arco circular quando esse comprimento L é calculado assim:
L = 4 × bronzeado(α / 4) / 3
A ilustração mostra um ângulo de 45 graus, então L é igual a 0,265. No código, esse valor seria multiplicado pelo raio desejado do círculo.
A página Arco Circular de Bezier permite que você experimente definir uma curva de Bézier para aproximar um arco circular para ângulos que variam até 180 graus. O arquivo BezierCircularArcPage.xaml instancia o SKCanvasView e a Slider para selecionar o ângulo. O PaintSurface manipulador de eventos no arquivo code-behind BezierCircularArgPage.xaml.cs usa uma transformação para definir o ponto (0, 0) para o centro da tela. Ele desenha um círculo centrado nesse ponto para comparação e, em seguida, calcula os dois pontos de controle para a curva de Bézier:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Translate to center
canvas.Translate(info.Width / 2, info.Height / 2);
// Draw the circle
float radius = Math.Min(info.Width, info.Height) / 3;
canvas.DrawCircle(0, 0, radius, blackStroke);
// Get the value of the Slider
float angle = (float)angleSlider.Value;
// Calculate length of control point line
float length = radius * 4 * (float)Math.Tan(Math.PI * angle / 180 / 4) / 3;
// Calculate sin and cosine for half that angle
float sin = (float)Math.Sin(Math.PI * angle / 180 / 2);
float cos = (float)Math.Cos(Math.PI * angle / 180 / 2);
// Find the end points
SKPoint point0 = new SKPoint(-radius * sin, radius * cos);
SKPoint point3 = new SKPoint(radius * sin, radius * cos);
// Find the control points
SKPoint point0Normalized = Normalize(point0);
SKPoint point1 = point0 + new SKPoint(length * point0Normalized.Y,
-length * point0Normalized.X);
SKPoint point3Normalized = Normalize(point3);
SKPoint point2 = point3 + new SKPoint(-length * point3Normalized.Y,
length * point3Normalized.X);
// Draw the points
canvas.DrawCircle(point0.X, point0.Y, 10, blackFill);
canvas.DrawCircle(point1.X, point1.Y, 10, blackFill);
canvas.DrawCircle(point2.X, point2.Y, 10, blackFill);
canvas.DrawCircle(point3.X, point3.Y, 10, blackFill);
// Draw the tangent lines
canvas.DrawLine(point0.X, point0.Y, point1.X, point1.Y, dottedStroke);
canvas.DrawLine(point3.X, point3.Y, point2.X, point2.Y, dottedStroke);
// Draw the Bezier curve
using (SKPath path = new SKPath())
{
path.MoveTo(point0);
path.CubicTo(point1, point2, point3);
canvas.DrawPath(path, redStroke);
}
}
// Vector methods
SKPoint Normalize(SKPoint v)
{
float magnitude = Magnitude(v);
return new SKPoint(v.X / magnitude, v.Y / magnitude);
}
float Magnitude(SKPoint v)
{
return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);
}
Os pontos inicial e final (point0 e point3) são calculados com base nas equações paramétricas normais para o círculo. Como o círculo está centrado em (0, 0), esses pontos também podem ser tratados como vetores radiais do centro do círculo até a circunferência. Os pontos de controle estão em linhas tangente ao círculo, portanto estão em ângulos retos com esses vetores radiais. Um vetor em ângulo reto com outro é simplesmente o vetor original com as coordenadas X e Y trocadas e uma delas tornada negativa.
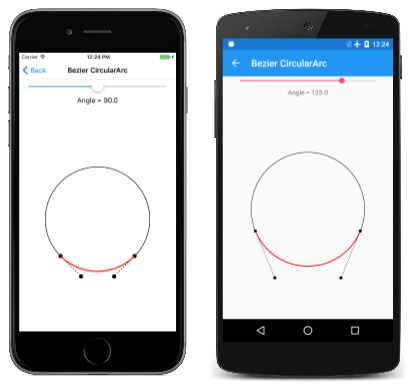
Aqui está o programa em execução com diferentes ângulos:
Olhe atentamente para a terceira captura de tela, e você verá que a curva de Bézier se desvia notavelmente de um semicírculo quando o ângulo é de 180 graus, mas a tela do iOS mostra que parece se encaixar bem em um quarto de círculo quando o ângulo é de 90 graus.
Calcular as coordenadas dos dois pontos de controle é bastante fácil quando o quarto círculo é orientado assim:
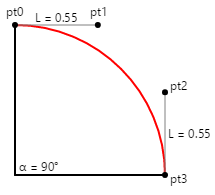
Se o raio do círculo é 100, então L é 55, e esse é um número fácil de lembrar.
A página Quadratura do Círculo anima uma figura entre um círculo e um quadrado. O círculo é aproximado por quatro curvas de Bézier cujas coordenadas são mostradas na primeira coluna desta definição de matriz na SquaringTheCirclePage classe:
public class SquaringTheCirclePage : ContentPage
{
SKPoint[,] points =
{
{ new SKPoint( 0, 100), new SKPoint( 0, 125), new SKPoint() },
{ new SKPoint( 55, 100), new SKPoint( 62.5f, 62.5f), new SKPoint() },
{ new SKPoint( 100, 55), new SKPoint( 62.5f, 62.5f), new SKPoint() },
{ new SKPoint( 100, 0), new SKPoint( 125, 0), new SKPoint() },
{ new SKPoint( 100, -55), new SKPoint( 62.5f, -62.5f), new SKPoint() },
{ new SKPoint( 55, -100), new SKPoint( 62.5f, -62.5f), new SKPoint() },
{ new SKPoint( 0, -100), new SKPoint( 0, -125), new SKPoint() },
{ new SKPoint( -55, -100), new SKPoint(-62.5f, -62.5f), new SKPoint() },
{ new SKPoint(-100, -55), new SKPoint(-62.5f, -62.5f), new SKPoint() },
{ new SKPoint(-100, 0), new SKPoint( -125, 0), new SKPoint() },
{ new SKPoint(-100, 55), new SKPoint(-62.5f, 62.5f), new SKPoint() },
{ new SKPoint( -55, 100), new SKPoint(-62.5f, 62.5f), new SKPoint() },
{ new SKPoint( 0, 100), new SKPoint( 0, 125), new SKPoint() }
};
...
}
A segunda coluna contém as coordenadas de quatro curvas de Bézier que definem um quadrado cuja área é aproximadamente a mesma que a área do círculo. (Desenhar um quadrado com a área exata como um determinado círculo é o clássico problema geométrico insolúvel da quadratura do círculo.) Para renderizar um quadrado com curvas de Bézier, os dois pontos de controle para cada curva são os mesmos, e eles são colineares com os pontos inicial e final, de modo que a curva de Bézier é renderizada como uma linha reta.
A terceira coluna da matriz é para valores interpolados para uma animação. A página define um temporizador para 16 milissegundos e o PaintSurface manipulador é chamado nessa taxa:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.Scale(Math.Min(info.Width / 300, info.Height / 300));
// Interpolate
TimeSpan timeSpan = new TimeSpan(DateTime.Now.Ticks);
float t = (float)(timeSpan.TotalSeconds % 3 / 3); // 0 to 1 every 3 seconds
t = (1 + (float)Math.Sin(2 * Math.PI * t)) / 2; // 0 to 1 to 0 sinusoidally
for (int i = 0; i < 13; i++)
{
points[i, 2] = new SKPoint(
(1 - t) * points[i, 0].X + t * points[i, 1].X,
(1 - t) * points[i, 0].Y + t * points[i, 1].Y);
}
// Create the path and draw it
using (SKPath path = new SKPath())
{
path.MoveTo(points[0, 2]);
for (int i = 1; i < 13; i += 3)
{
path.CubicTo(points[i, 2], points[i + 1, 2], points[i + 2, 2]);
}
path.Close();
canvas.DrawPath(path, cyanFill);
canvas.DrawPath(path, blueStroke);
}
}
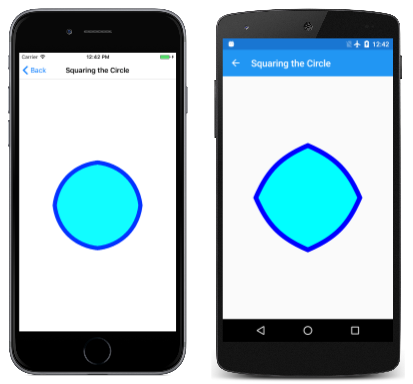
Os pontos são interpolados com base em um valor sinusoidal oscilante de t. Os pontos interpolados são então usados para construir uma série de quatro curvas de Bézier conectadas. Aqui está a animação em execução:
Tal animação seria impossível sem curvas que são algoritmicamente flexíveis o suficiente para serem renderizadas como arcos circulares e linhas retas.
A página Bezier Infinity também aproveita a capacidade de uma curva de Bézier para aproximar um arco circular. Aqui está o PaintSurface manipulador da BezierInfinityPage classe:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPath path = new SKPath())
{
path.MoveTo(0, 0); // Center
path.CubicTo( 50, -50, 95, -100, 150, -100); // To top of right loop
path.CubicTo( 205, -100, 250, -55, 250, 0); // To far right of right loop
path.CubicTo( 250, 55, 205, 100, 150, 100); // To bottom of right loop
path.CubicTo( 95, 100, 50, 50, 0, 0); // Back to center
path.CubicTo( -50, -50, -95, -100, -150, -100); // To top of left loop
path.CubicTo(-205, -100, -250, -55, -250, 0); // To far left of left loop
path.CubicTo(-250, 55, -205, 100, -150, 100); // To bottom of left loop
path.CubicTo( -95, 100, -50, 50, 0, 0); // Back to center
path.Close();
SKRect pathBounds = path.Bounds;
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.Scale(0.9f * Math.Min(info.Width / pathBounds.Width,
info.Height / pathBounds.Height));
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Blue;
paint.StrokeWidth = 5;
canvas.DrawPath(path, paint);
}
}
}
Pode ser um bom exercício traçar essas coordenadas em papel gráfico para ver como elas estão relacionadas. O sinal do infinito está centrado em torno do ponto (0, 0), e os dois laços têm centros de (–150, 0) e (150, 0) e raios de 100. Na série de CubicTo comandos, você pode ver coordenadas X de pontos de controle assumindo valores de –95 e –205 (esses valores são –150 mais e menos 55), 205 e 95 (150 mais e menos 55), bem como 250 e –250 para os lados direito e esquerdo. A única exceção é quando o signo do infinito se cruza no centro. Nesse caso, os pontos de controle têm coordenadas com uma combinação de 50 e –50 para endireitar a curva perto do centro.
Aqui está o sinal do infinito:
É um pouco mais suave em direção ao centro do que o sinal de infinito renderizado pela página Arc Infinity do artigo Três Maneiras de Desenhar um Arco.
A Curva Quadrática de Bézier
A curva de Bézier quadrática tem apenas um ponto de controle, e a curva é definida por apenas três pontos: o ponto inicial, o ponto de controle e o ponto final. As equações paramétricas são muito semelhantes à curva cúbica de Bézier, exceto que o expoente mais alto é 2, então a curva é um polinômio quadrático:
x(t) = (1 – t)²x₀ + 2t(1 – t)x₁ + t²x₂
y(t) = (1 – t)²y₀ + 2t(1 – t)y₁ + t²y₂
Para adicionar uma curva de Bézier quadrática a um caminho, use o QuadTo método ou a QuadTo sobrecarga com coordenadas e y separadasx:
public void QuadTo (SKPoint point1, SKPoint point2)
public void QuadTo (Single x1, Single y1, Single x2, Single y2)
Os métodos adicionam uma curva da posição atual para point2 com point1 como o ponto de controle.
Você pode experimentar curvas de Bézier quadráticas com a página Curva Quadrática, que é muito semelhante à página Curva de Bezier, exceto que tem apenas três pontos de toque. Aqui está o PaintSurface manipulador no arquivo code-behind QuadraticCurve.xaml.cs :
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with quadratic Bezier
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.QuadTo(touchPoints[1].Center,
touchPoints[2].Center);
canvas.DrawPath(path, strokePaint);
}
// Draw tangent lines
canvas.DrawLine(touchPoints[0].Center.X,
touchPoints[0].Center.Y,
touchPoints[1].Center.X,
touchPoints[1].Center.Y, dottedStrokePaint);
canvas.DrawLine(touchPoints[1].Center.X,
touchPoints[1].Center.Y,
touchPoints[2].Center.X,
touchPoints[2].Center.Y, dottedStrokePaint);
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
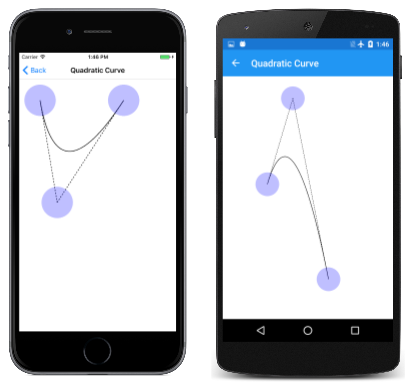
E aqui está correndo:
As linhas pontilhadas são tangente à curva no ponto inicial e no ponto final, e se encontram no ponto de controle.
O Bézier quadrático é bom se você precisa de uma curva de uma forma geral, mas você prefere a conveniência de apenas um ponto de controle em vez de dois. O Bézier quadrático renderiza de forma mais eficiente do que qualquer outra curva, e é por isso que é usado internamente no Skia para renderizar arcos elípticos.
No entanto, a forma de uma curva de Bézier quadrática não é elíptica, razão pela qual múltiplos Béziers quadráticos são necessários para aproximar um arco elíptico. O Bézier quadrático é antes um segmento de uma parábola.
A curva cônica de Bézier
A curva cônica de Bézier — também conhecida como curva de Bézier quadrática racional — é uma adição relativamente recente à família das curvas de Bézier. Como a curva de Bézier quadrática, a curva de Bézier quadrática racional envolve um ponto de partida, um ponto final e um ponto de controle. Mas a curva de Bézier quadrática racional também requer um valor de peso . É chamado de quadrático racional porque as fórmulas paramétricas envolvem proporções.
As equações paramétricas para X e Y são razões que compartilham o mesmo denominador. Aqui está a equação para o denominador para t variando de 0 a 1 e um valor de peso de w:
d(t) = (1 – t)² + 2wt(1 – t) + t²
Em teoria, uma quadrática racional pode envolver três valores de peso separados, um para cada um dos três termos, mas estes podem ser simplificados para apenas um valor de peso no médio prazo.
As equações paramétricas para as coordenadas X e Y são semelhantes às equações paramétricas para o Bézier quadrático, exceto que o termo médio também inclui o valor do peso, e a expressão é dividida pelo denominador:
x(t) = ((1 – t)²x₀ + 2wt(1 – t)x₁ + t²x₂)) ÷ d(t)
y(t) = ((1 – t)²y₀ + 2wt(1 – t)y₁ + t²y₂)) ÷ d(t)
As curvas de Bézier quadráticas racionais também são chamadas de cônicas porque podem representar exatamente segmentos de qualquer seção cônica — hipérboles, parábolas, elipses e círculos.
Para adicionar uma curva de Bézier quadrática racional a um caminho, use o ConicTo método ou a ConicTo sobrecarga com coordenadas e y separadasx:
public void ConicTo (SKPoint point1, SKPoint point2, Single weight)
public void ConicTo (Single x1, Single y1, Single x2, Single y2, Single weight)
Observe o parâmetro final weight .
A página Curva Cônica permite que você experimente essas curvas. A classe ConicCurvePage deriva de InteractivePage. O arquivo ConicCurvePage.xaml instancia a Slider para selecionar um valor de peso entre –2 e 2. O arquivo code-behind ConicCurvePage.xaml.cs cria três TouchPoint objetos, e o PaintSurface manipulador simplesmente renderiza a curva resultante com as linhas tangentes aos pontos de controle:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with conic curve
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.ConicTo(touchPoints[1].Center,
touchPoints[2].Center,
(float)weightSlider.Value);
canvas.DrawPath(path, strokePaint);
}
// Draw tangent lines
canvas.DrawLine(touchPoints[0].Center.X,
touchPoints[0].Center.Y,
touchPoints[1].Center.X,
touchPoints[1].Center.Y, dottedStrokePaint);
canvas.DrawLine(touchPoints[1].Center.X,
touchPoints[1].Center.Y,
touchPoints[2].Center.X,
touchPoints[2].Center.Y, dottedStrokePaint);
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
Aqui está em execução:
Como você pode ver, o ponto de controle parece puxar a curva em direção a ele mais quando o peso é maior. Quando o peso é zero, a curva se torna uma linha reta do ponto inicial ao ponto final.
Em teoria, pesos negativos são permitidos e fazem com que a curva se afaste do ponto de controle. No entanto, pesos de –1 ou abaixo fazem com que o denominador nas equações paramétricas se torne negativo para valores particulares de t. Provavelmente por essa razão, pesos negativos são ignorados nos ConicTo métodos. O programa Conic Curve permite que você defina pesos negativos, mas como você pode ver experimentando, pesos negativos têm o mesmo efeito que um peso de zero e fazem com que uma linha reta seja renderizada.
É muito fácil derivar o ponto de controle e o peso para usar o ConicTo método para desenhar um arco circular até (mas não incluindo) um semicírculo. No diagrama a seguir, as linhas tangentes dos pontos inicial e final se encontram no ponto de controle.
Você pode usar trigonometria para determinar a distância do ponto de controle do centro do círculo: É o raio do círculo dividido pelo cosseno da metade do ângulo α. Para desenhar um arco circular entre os pontos inicial e final, defina o peso para o mesmo cosseno da metade do ângulo. Observe que se o ângulo é de 180 graus, então as linhas tangentes nunca se encontram e o peso é zero. Mas para ângulos inferiores a 180 graus, a matemática funciona bem.
A página Arco Circular Cônico demonstra isso. O arquivo ConicCircularArc.xaml instancia um Slider para selecionar o ângulo. O PaintSurface manipulador no arquivo code-behind ConicCircularArc.xaml.cs calcula o ponto de controle e o peso:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Translate to center
canvas.Translate(info.Width / 2, info.Height / 2);
// Draw the circle
float radius = Math.Min(info.Width, info.Height) / 4;
canvas.DrawCircle(0, 0, radius, blackStroke);
// Get the value of the Slider
float angle = (float)angleSlider.Value;
// Calculate sin and cosine for half that angle
float sin = (float)Math.Sin(Math.PI * angle / 180 / 2);
float cos = (float)Math.Cos(Math.PI * angle / 180 / 2);
// Find the points and weight
SKPoint point0 = new SKPoint(-radius * sin, radius * cos);
SKPoint point1 = new SKPoint(0, radius / cos);
SKPoint point2 = new SKPoint(radius * sin, radius * cos);
float weight = cos;
// Draw the points
canvas.DrawCircle(point0.X, point0.Y, 10, blackFill);
canvas.DrawCircle(point1.X, point1.Y, 10, blackFill);
canvas.DrawCircle(point2.X, point2.Y, 10, blackFill);
// Draw the tangent lines
canvas.DrawLine(point0.X, point0.Y, point1.X, point1.Y, dottedStroke);
canvas.DrawLine(point2.X, point2.Y, point1.X, point1.Y, dottedStroke);
// Draw the conic
using (SKPath path = new SKPath())
{
path.MoveTo(point0);
path.ConicTo(point1, point2, weight);
canvas.DrawPath(path, redStroke);
}
}
Como você pode ver, não há diferença visual entre o ConicTo caminho mostrado em vermelho e o círculo subjacente exibido para referência:
Mas defina o ângulo para 180 graus, e a matemática falha.
É lamentável neste caso que ConicTo não suporte pesos negativos, porque em teoria (com base nas equações paramétricas), o círculo pode ser completado com outra chamada para ConicTo com os mesmos pontos, mas um valor negativo do peso. Isso permitiria criar um círculo inteiro com apenas duas ConicTo curvas com base em qualquer ângulo entre (mas não incluindo) zero graus e 180 graus.