series_fit_poly()
Aplica-se a: ✅Microsoft Fabric✅Azure Data Explorer✅Azure Monitor✅Microsoft Sentinel
Aplica uma regressão polinomial de uma variável independente (x_series) a uma variável dependente (y_series). Essa função usa uma tabela contendo várias séries (matrizes numéricas dinâmicas) e gera o polinômio de alta ordem mais adequado para cada série usando regressão polinomial.
Dica
- Para regressão linear de uma série uniformemente espaçada, conforme criado pelo operador make-series, use a função mais simples series_fit_line(). Veja o Exemplo 2.
- Se x_series for fornecido e a regressão for feita em alto grau, considere normalizar para o intervalo [0-1]. Veja o Exemplo 3.
- Se x_series for do tipo datetime, ele deverá ser convertido em double e normalizado. Veja o Exemplo 3.
- Para referência à implementação de regressão polinomial usando Python embutido, consulte series_fit_poly_fl().
Sintaxe
T | extend series_fit_poly( y_series [, grau x_series,])
Saiba mais sobre as convenções de sintaxe.
Parâmetros
| Nome | Digitar | Obrigatória | Descrição |
|---|---|---|---|
| y_series | dynamic |
✔️ | Uma matriz de valores numéricos que contém a variável dependente. |
| x_series | dynamic |
Uma matriz de valores numéricos que contém a variável independente. Necessário apenas para séries com espaçamento desigual. Se não for especificado, ele será definido como um valor padrão de [1, 2, ..., length(y_series)]. | |
| grau | A ordem necessária do polinômio para caber. Por exemplo, 1 para regressão linear, 2 para regressão quadrática e assim por diante. O padrão é 1, o que indica regressão linear. |
Devoluções
A series_fit_poly() função retorna as seguintes colunas:
rsquare: r-square é uma medida padrão da qualidade do ajuste. O valor é um número no intervalo [0-1], em que 1 - é o melhor ajuste possível e 0 significa que os dados não estão ordenados e não se ajustam a nenhuma linha.coefficients: Matriz numérica contendo os coeficientes do polinômio mais bem ajustado com o grau dado, ordenados do coeficiente de potência mais alto para o mais baixo.variance: Variância da variável dependente (y_series).rvariance: Variância residual que é a variância entre os valores dos dados de entrada e os aproximados.poly_fit: Matriz numérica contendo uma série de valores do polinômio mais bem ajustado. O comprimento da série é igual ao comprimento da variável dependente (y_series). O valor é usado para gráficos.
Exemplos
Exemplo 1
Um polinômio de quinta ordem com ruído nos eixos x e y:
range x from 1 to 200 step 1
| project x = rand()*5 - 2.3
| extend y = pow(x, 5)-8*pow(x, 3)+10*x+6
| extend y = y + (rand() - 0.5)*0.5*y
| summarize x=make_list(x), y=make_list(y)
| extend series_fit_poly(y, x, 5)
| project-rename fy=series_fit_poly_y_poly_fit, coeff=series_fit_poly_y_coefficients
|fork (project x, y, fy) (project-away x, y, fy)
| render linechart
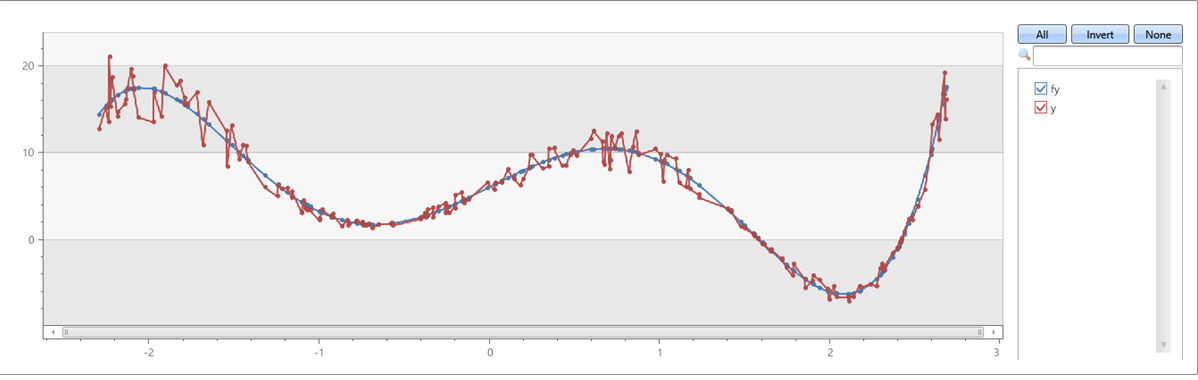
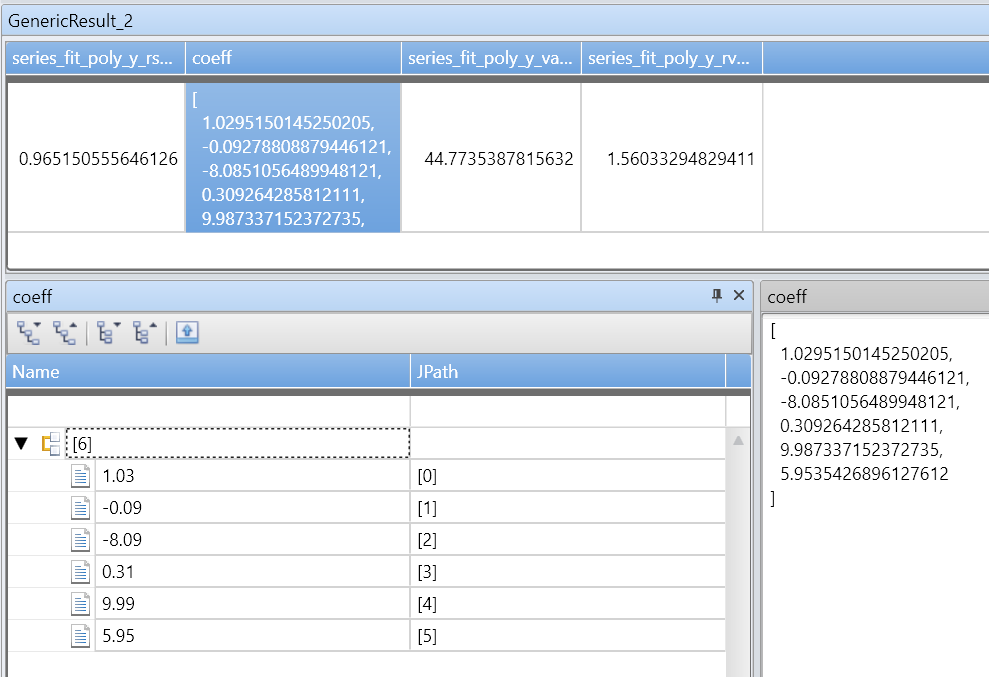
Exemplo 2
Verifique se series_fit_poly com degree=1 corresponde series_fit_line:
demo_series1
| extend series_fit_line(y)
| extend series_fit_poly(y)
| project-rename y_line = series_fit_line_y_line_fit, y_poly = series_fit_poly_y_poly_fit
| fork (project x, y, y_line, y_poly) (project-away id, x, y, y_line, y_poly)
| render linechart with(xcolumn=x, ycolumns=y, y_line, y_poly)
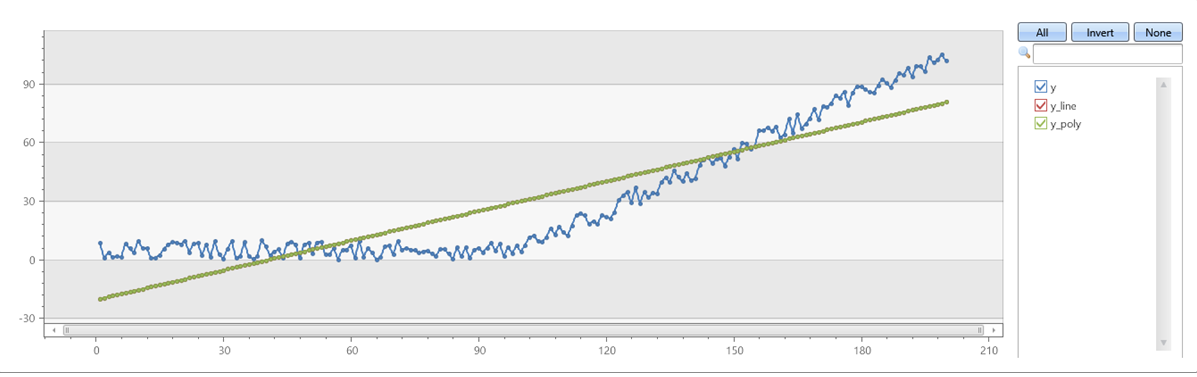

Exemplo 3
Séries temporais irregulares (espaçadas de forma desigual):
//
// x-axis must be normalized to the range [0-1] if either degree is relatively big (>= 5) or original x range is big.
// so if x is a time axis it must be normalized as conversion of timestamp to long generate huge numbers (number of 100 nano-sec ticks from 1/1/1970)
//
// Normalization: x_norm = (x - min(x))/(max(x) - min(x))
//
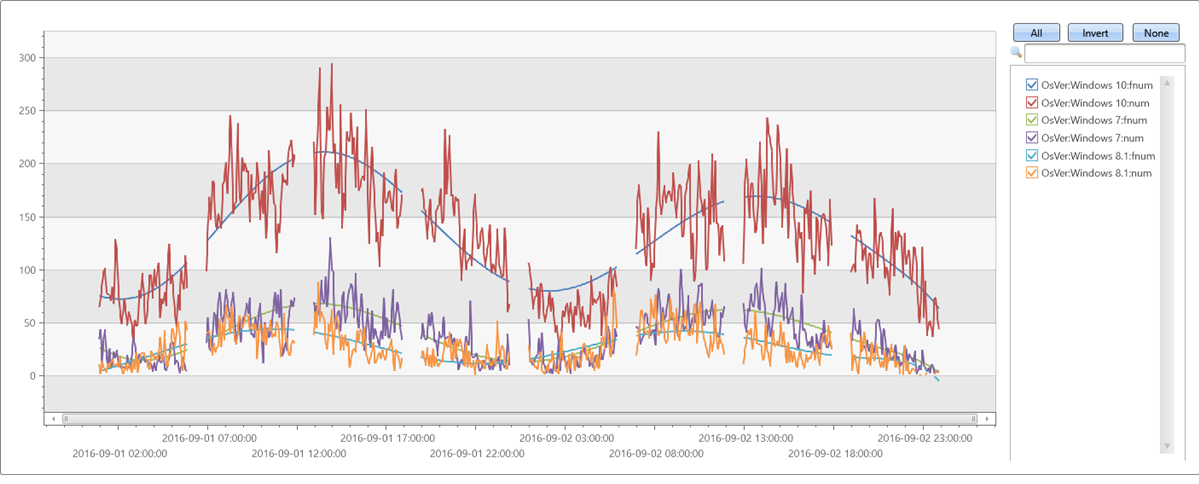
irregular_ts
| extend series_stats(series_add(TimeStamp, 0)) // extract min/max of time axis as doubles
| extend x = series_divide(series_subtract(TimeStamp, series_stats__min), series_stats__max-series_stats__min) // normalize time axis to [0-1] range
| extend series_fit_poly(num, x, 8)
| project-rename fnum=series_fit_poly_num_poly_fit
| render timechart with(ycolumns=num, fnum)