System.Drawing.Drawing2D.Matrix classe
Este artigo fornece observações complementares à documentação de referência para essa API.
A Matrix classe encapsula uma matriz afim 3 por 3 que representa uma transformação geométrica.
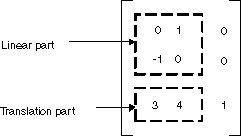
No GDI+, você pode armazenar uma transformação afim em um Matrix objeto. Como a terceira coluna de uma matriz que representa uma transformação afim é sempre (0, 0, 1), você especifica apenas os seis números nas duas primeiras colunas ao construir um Matrix objeto. A instrução Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) constrói a matriz mostrada na figura a seguir.
Observação
No .NET 6 e versões posteriores, o pacote System.Drawing.Common, que inclui esse tipo, só tem suporte em sistemas operacionais Windows. O uso desse tipo em aplicativos de plataforma cruzada causa avisos de tempo de compilação e exceções de tempo de execução. Para obter mais informações, consulte System.Drawing.Common suportado apenas no Windows.
Transformações compostas
Uma transformação de composição é uma sequência de transformações, uma seguida da outra. Considere as matrizes e transformações na lista a seguir:
| Matriz | Transformação |
|---|---|
| Matriz A | Girar 90 graus |
| Matriz B | Dimensionar por um fator de 2 na direção x |
| Matriz C | Mover 3 unidades na direção y |
Se você começar com o ponto (2, 1) - representado pela matriz [2 1 1] - e multiplicar por A, depois B, então C, o ponto (2, 1) sofrerá as três transformações na ordem listada.
[2 1 1]ABC = [-2 5 1]
Em vez de armazenar as três partes da transformação de composição em três matrizes separadas, você pode multiplicar A, B e C juntos para obter uma única matriz 3 × 3 que armazena a transformação de composição inteira. Suponha que ABC = D. Então um ponto multiplicado por D dá o mesmo resultado que um ponto multiplicado por A, depois B, depois C.
[2 1 1]D = [-2 5 1]
A ilustração a seguir mostra as matrizes A, B, C e D.
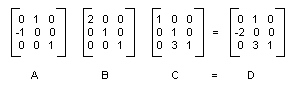
O fato de que a matriz de uma transformação composta pode ser formada multiplicando as matrizes de transformação individuais significa que qualquer sequência de transformações afins pode ser armazenada em um único Matrix objeto.
Cuidado
A ordem de uma transformação de composição é importante. Em geral, girar, dimensionar e converter não é o mesmo que dimensionar, girar e converter. Da mesma forma, a ordem de multiplicação de matriz é importante. Em geral, ABC não é o mesmo que BAC.
A Matrix classe fornece vários métodos para criar uma transformação composta: Multiply, Rotate, RotateAt, Scale, Sheare Translate. O exemplo a seguir cria a matriz de uma transformação de composição que primeiro gira 30 graus e, então, é dimensionada por um fator de 2 na direção y e movida em 5 unidades na direção x:
Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);
Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)
