Compartilhar via

クォータニオンってなに？

  • Artigo

クォータニオンでボーン処理、その１:クォータニオンってなに？

クォータニオンの前知識なしでクォータニオンを使ったスキニングアニメーションのコードを理解するのは厳しいので、今回から数回に分けてクォータニオンを説明していきます。

クォータニオン(Quaterinon)は日本語で四元数(しげんすう)と言い、定義的には3つの虚数単位を持つ超複素数系のひとつです。

………

と、いってもなんのことかさっぱり解らなくても大丈夫です(たぶん)。本来であれば数学的な説明も入れるべきですが、今回はスキンアニメーションでの使われ方の説明なので、そういった部分は割愛します。より詳しく数学的な意味が知りたい人は「超複素数入門」、どの様に回転を表すかを知るためには英語ですが「Quaternions and Rotation Sequences」が良書ですし、日本語でも「実例で学ぶゲーム3D数学」が参考になると思います。

クォータニオンを簡単に説明すると、回転行列の変わりに使える便利な道具です。

行列の中で回転を表す部分は以下のようにRの部分、つまり3x3、9個の数値であらわします。XNAフレームワークの中では9個のfloatになります。

mtx

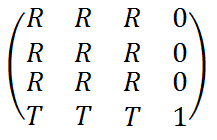
これがクォータニオンでは4個の数値、XNAフレームワーク内では4個のfloatで同じ回転を表すことができます。つまり、回転を表すのに必要なメモリが半分以下になる訳です。メモリ消費量だけで比べるのならx,y,z軸の回転角度を持つほうがより少ない消費量になりますが、オイラー角を使った場合、線形補間ができなかったり、行列への変換に三角関数を使う必要があったり、なにより面倒なジンバルロックの問題があったりと実際のゲーム開発では回転する範囲が制限されている場合以外ではオイラー角による回転が使われることは少なく、クォータニオンが使われるケースがほとんどです。

クォータニオンの利点をまとめると

  1. メモリ使用量が少ない、回転行列の半分、4x4の行列の1/4
  2. 行列と同じように線形補間(Learp)、または球面線形補間(Slerp)ができる
  3. 行列への変換がオイラー角を使うのに比べて高速
  4. ジンバルロックに悩まされない
  5. 正規化が簡単

と、いった感じになりますが、弱点としては

  1. オイラー角で回転をもつよりメモリ使用量が少し増える
  2. オイラー角と違って直感的に解りづらい

があります。

次回はXNAフレームワーク内でどのようにクォータニオンを使うのかを説明します。

Comments