STBuffer() и BufferWithCurves()
1. В предыдущем посте мы покрывали Москву кругами, составленными при помощи метода STBuffer(distance). На самом деле он рисует не круги, а полигоны. Метод STBuffer() является стандартным методом ОGC и существовал еще в SQL Server 2008, где ни о каких кругах речь не шла. Метод STBuffer() аппроксимирует круг при помощи многоугольника с достаточным количеством вершин. Пример:
--Рисуем типа круг радиусом 1000 м
declare @типаКруг geography = geography::Point(55.755831, 37.617673, 4326).STBuffer(1000)
select @типаКруг, @типаКруг.STNumPoints(), @типаКруг.STAsText()
-------------------------------------------------------------------------------------------------------------------------
129
POLYGON ((37.628949076957575 55.762174734892838, 37.628383456950111 55.762479100751563, ..., 37.628949076957575 55.762174734892838))
Рис. 1
В действительности вершин будет не 129, а 128. Многоугольник имеет замкнутый контур, так что его граница оканчивается на ту же вершину, с которой начинается, как можно видеть из результата STAsText().
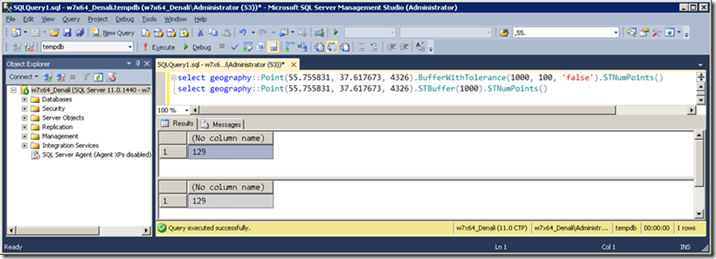
Чтобы понять, что значит "достаточное количество вершин", рассмотрим родственный метод BufferWithTolerance(distance, tolerance, relative), который также определен как для геометрии, так и для географии, однако в отличие от STBuffer является неканоническим. По сравнению с STBuffer он, кроме радиуса, имеет в качестве параметра погрешность - tolerance . Чем меньше погрешность, тем из большего количества точек будет состоять аппроксимирующий многоугольник. Третий параметр - relative - определяет является ли погрешность относительной или абсолютной. 0 или 'false' - абсолютная погрешность - означает, что потребуется столько точек, чтобы максимальное отклонение от идеальной окружности не превышало tolerance. 1 или 'true' - относительная погрешность - получается как абсолютная делить на диаметр фигуры, т.е. максимальное расстояние между ее точками. Точно определять диаметр SQL Server пока не научился, поэтому, насколько я понимаю, в случае геометрии за диаметр он принимает диагональ STEnvelope. В случае географии диаметр фигуры считается как ее максимальный угловой размер в радианах (см. пост EnvelopeCenter и EnvelopeAngle) умножить на экваториальный радиус эллипсоида, обозначающего Землю. Кстати, в Denali CTP3 BufferWithTolerance() в географии не работает. Неважно, какую указать погрешность и относительность, получится ровно то же, что и STBuffer().
Рис.2
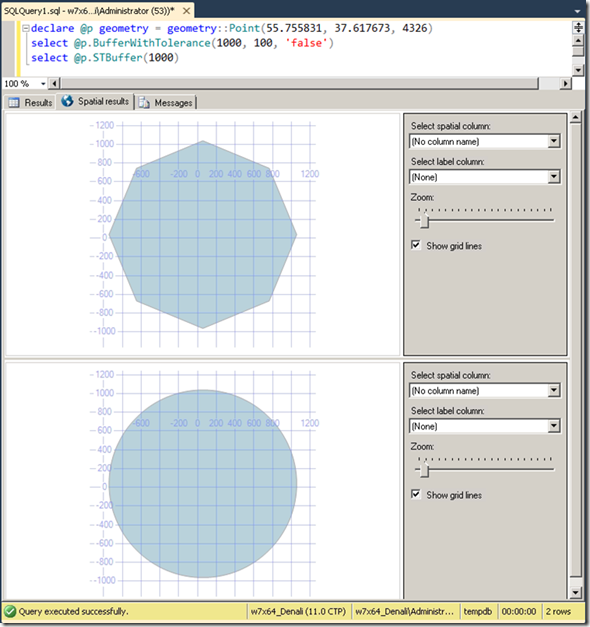
Мужики в курсе, обещали пофиксить к RC0. Пока посмотрим, как это должно работать, на примере геометрии:
Рис.3
Опытным путем можно определить, что STBuffer(distance) - это BufferWithTolerance(distance, 0.001, 1) независимо от distance. Для интереса сравните STNumPoints() у обоих, как на Рис.2. Потом можно внимательно прочитать документацию и обнаружить, что примерно то же в ней написано: метод STBuffer() вычисляет буфер аналогично методам BufferWithTolerance, задавая аргументы tolerance = distance * 0,001 и relative = false. Разница в том, что в BOL опечатка - аргумент relative, конечно, по смыслу должен равняться true. Как известно, настоящие программеры мануалов не читают, действуя методом научного тыка. Иногда это оправдано.
2. В Denali появилась нормальная поддержка дуг (CIRCULARSTRING), поэтому надобность в STBuffer при рисовании окружностей отпадает. При помощи метода BufferWithCurves(distance), который поддерживается как в геометрии, так и в географии, можно нарисовать честный круг, а не аппроксимирующий его многоугольник. Внешней границей круга является дуга, обозначающая полную окружность. Правда, имеет место еще один нюанс. Дуги появились раньше, чем SSMS научилась их рисовать, поэтому закладку Spatial Results в панели результатов из нее в СТР1 убрали, чтобы не возникало лишних вопросов. Как написано здесь уважаемыми людьми, for SQL Server Code-Named “Denali” CTP3, the Spatial results tab is available and handles the new features which SQL Server Code-Named “Denali” CTP1 introduced (FullGlobe, circular arcs, etc.) Ребята погорячились. Закладка Spatial Results в СТР3 действительно появилась, но дуги она рисовать по-прежнему не умеет:
declare @круг geography = geography::Point(55.755831, 37.617673, 4326).BufferWithCurves(1000)
select @круг.ToString(), @круг.RingN(1).ToString()
select @круг
select @круг.RingN(1)
-------------------------------------------------------------------------------------------------------------------------
Это круг в текстовом представлении
CURVEPOLYGON (CIRCULARSTRING (37.628949076957575 55.762174734892838, 37.606396923042439 55.762174734892838, 37.606400579105681 55.749486226550012, 37.628945420894325 55.749486226550019, 37.628949076957575 55.762174734892838))
Это его внешняя окружность
CIRCULARSTRING (37.628949076957575 55.762174734892838, 37.606396923042439 55.762174734892838, 37.606400579105681 55.749486226550012, 37.628945420894325 55.749486226550019, 37.628949076957575 55.762174734892838)
Это SSMS в СТР3 не умеет их рисовать:
Рис.4
На помощь приходит метод STCurveToLine(), аппроксимирующий дугу ломаной подобно тому, как круг аппроксимируется многоугольником в рассмотренном выше методе STBuffer.
declare @типаКруг geography = geography::Point(55.755831, 37.617673, 4326).BufferWithCurves(1000).STCurveToLine()
select @типаКруг
select @типаКруг.STNumPoints(), @типаКруг.STAsText()
-------------------------------------------------------------------------------------------------------------------------
129
POLYGON ((37.628949076957575 55.762174734892838, 37.628383456950111 55.76247910075157, …, 37.628949076957575 55.762174734892838))
Рис.5
Сравнив результаты с Рис.1, возникает предположение, что STBuffer(distance) = BufferWithCurves(distance).STCurveToLine(). Проверим, так ли это, при помощи метода STEquals():
declare @p geography = geography::Point(55.755831, 37.617673, 4326), @r float = 1000
select @p.BufferWithCurves(@r).STCurveToLine().STEquals(@p.STBuffer(@r))
-------------------------------------------------------------------------------------------------------------------------
0
Рис.6
Ан нет. Можно посмотреть, в чем именно заключается симметрическая разность двух множеств, иными словами, объединение минус пересечение, иными словами, что из первой фигуры не входит во вторую плюс что из второй не входит в первую при помощи метода STSymDifference(), но она получается настолько мизерная, что проще выписать рядом текстовое представление результатов Рис.1 и Рис.5 и сравнить:
POLYGON ((37.628949076957575 55.762174734892838, 37.628383456950111 55.762479100751563, 37.627792021343673 55.76276744915171, 37.627176195145005 55.76303908507596, ...
POLYGON ((37.628949076957575 55.762174734892838, 37.628383456950111 55.76247910075157, 37.627792021343673 55.76276744915171, 37.627176195145005 55.763039085075967, ...
Рис.7
Жирным цветом показаны расхождения. Мы видим, что результаты очень близки. Расхождения, скорее всего, вызваны погрешностями округления. Тем не менее, с формальной точки зрения это все-таки разные фигуры.
3. Существует также метод CurveToLineWithTolerance(tolerance, relative), который соотносится с STCurveToLine() так же, как рассмотренный выше BufferWithTolerance(distance, tolerance, relative) с STBuffer(distance).
К толерантным методам по смысловой близости плотно примыкает метод Reduce(tolerance). Если фигура прорисована детально, совершенно незачем для крупномасштабной карты хранить/рисовать все составляющие границу фигуры точки. Промежуточные и несущественные (те, что несильно отклоняют ее контур) можно выкинуть. К сожалению, параметра relative для Reduce не предусмотрено, поэтому tolerance должна задаваться в абсолютном выражении. Метод Reduce работает по известному алгоритму Дугласа-Пекера. В качестве примера упростим нарисованный в посте Ориентация полигона на поверхности \ Скрипт 1 внутримкадный многоугольник.
declare @s nvarchar(max) = (select Format(p.Lat, 'N8') + ' ' + Format(p.Long, 'N8') + ' ' from #mkad order by km desc for xml path(''))
set @s += (select top 1 Format(p.Lat, 'N8') + ' ' + Format(p.Long, 'N8') from #mkad order by km desc)
declare @m geography = geography::GeomFromGml('<Polygon xmlns="http://www.opengis.net/gml">
<exterior>
<LinearRing>
<posList>' + @s + '</posList>
</LinearRing>
</exterior>
</Polygon>', 4326)
select @m
select @m.Reduce(500)
select @m.Reduce(3000)
Рис.8
STNumPoints() возвращает, соответственно, 109, 16 и 9 по мере огрубления. Как мы помним из Рис.1, реальное кол-во вершин для многоугольников составляет STNumPoints() -(кол-во контуров границ = NumRing()). В геометрии метода NumRing() не предусмотрено, поэтому STNumPoints() - STNumInteriorRing() - 1.
4. В соответствии со стандартом OGC CIRCULARSTRING (дуга) задается тремя точками, т.к. три точки однозначно определяют проходящую через них окружность что на плоскости, что на поверхности сферы. Соответственно, CURVEPOLYGON (многоугольник, контуром которого выступают дуги или отрезки) определяется как минимум четырьмя точками, поскольку его внешняя или внутренние границы должны быть замкнуты, т.е. оканчиваться на ту же точку, с которой начались. Изобретенный OGC способ задания дуги лично мне представляется неестественным. Мне сложно представить практические задачи, в которых он был бы востребован. Более логичным, на мой взгляд, был бы способ задания дуги при помощи центра окружности, ее радиуса и начального и конечного углов, отсчитываемых от оси Х или меридиана в положительном направлении (против часовой стрелки), неважно. К тому же этот способ требует задания 5 величин, тогда как 3 поверхностные точки - это 6 координат. В одном из следующих постов я планирую по заданной дуге найти ее центр и радиус. Для геометрии это тривиально, можно сделать аналитически. В географии идея, в принципе, та же, но придется немного поупражняться в рисовании на поверхности Земли. Здесь в качестве затравки давайте решим обратную Рис.4 задачу: как, имея круг в виде CURVEPOLYGON (CIRCULARSTRING (37.628949076957575 55.762174734892838, 37.606396923042439 55.762174734892838, 37.606400579105681 55.749486226550012, 37.628945420894325 55.749486226550019, 37.628949076957575 55.762174734892838)), найти точку, являющуюся его центром. Я заметил, что сочетание параметров tolerance = 1 и relative = 'true' в методах CurveToLineWithTolerance и BufferWithTolerance всегда огрубляет круг до квадрата. Желающие могут вывести сие из определения tolerance и эмпирического, но вполне логичного факта, что точки при приближении окружности распределяются равномерно. Пересечение диагоналей вписанного в круг квадрата, т.е. отрезков, соединяющих 1-ю – 3-ю и 2-ю – 4-ю вершины, даст его центр.
declare @круг geography = geography::STGeomFromText('CURVEPOLYGON (CIRCULARSTRING (37.628949076957575 55.762174734892838, 37.606396923042439 55.762174734892838, 37.606400579105681 55.749486226550012, 37.628945420894325 55.749486226550019, 37.628949076957575 55.762174734892838))', 4326)
declare @вписанныйквадрат geography = @круг.CurveToLineWithTolerance(1, 1)
declare @диагональ1 geography = geography::STGeomFromText('LINESTRING(' + Format(@вписанныйквадрат.STPointN(1).Long, 'N14') + ' ' + Format(@вписанныйквадрат.STPointN(1).Lat, 'N14') + ',' +
Format(@вписанныйквадрат.STPointN(3).Long, 'N14') + ' ' + Format(@вписанныйквадрат.STPointN(3).Lat, 'N14') + ')', 4326)
declare @диагональ2 geography = geography::STGeomFromText('LINESTRING(' + Format(@вписанныйквадрат.STPointN(2).Long, 'N14') + ' ' + Format(@вписанныйквадрат.STPointN(2).Lat, 'N14') + ',' +
Format(@вписанныйквадрат.STPointN(4).Long, 'N14') + ' ' + Format(@вписанныйквадрат.STPointN(4).Lat, 'N14') + ')', 4326)
declare @центр geography = @диагональ1.STIntersection(@диагональ2)
select @центр.STAsText()
select @круг.STCurveToLine() union all select @вписанныйквадрат union all select @диагональ1 union all select @диагональ2 union all select @центр.STBuffer(25)
-------------------------------------------------------------------------------------------------------------------------
POINT (37.617672994144378 55.755830996704788)
Рис.9
Сравнивая с Рис.4-5 можно видеть, что центр окружности найден правильно с точностью до 6-го знака, как он изначально и задавался. Радиус, очевидно, находится как половина длины диагонали:
select @диагональ1.STLength()/2
-------------------------------------------------------------------------------------------------------------------------
1000.00000614389
Рис.10
5. В связи с возникшей в Денали поддержкой дуг и кругов мы рассматривали методы STBuffer/BufferWithTolerance/BufferWithCurves применительно к точке. Для полноты картины следует отметить, что при помощи этих методов можно изобразить эпсилон-окрестность не только точки, но и, вообще говоря, произвольной фигуры. Например, вот область в пределах километра по обе стороны МКАД, полученная в виде POLYGON при помощи метода STBuffer и в виде CURVEPOLYGON при помощи метода BufferWithCurves:
declare @s nvarchar(max) = (select Format(p.Lat, 'N8') + ' ' + Format(p.Long, 'N8') + ' ' from #mkad order by km desc for xml path(''))
set @s += (select top 1 Format(p.Lat, 'N8') + ' ' + Format(p.Long, 'N8') from #mkad order by km desc)
declare @m geography = geography::GeomFromGml('<Polygon xmlns="http://www.opengis.net/gml">
<exterior>
<LinearRing>
<posList>' + @s + '</posList>
</LinearRing>
</exterior>
</Polygon>', 4326)
select @m.RingN(1).STBuffer(1000), @m.RingN(1).STBuffer(1000).STAsText()
select @m.RingN(1).BufferWithCurves(1000).STCurveToLine(), @m.RingN(1).BufferWithCurves(1000).STAsText()
Рис.11
При желании из нее можно получить раздельно области в пределах километра как вне МКАД, так и внутри. В первом случае мы отнимаем от километровой окрестности дороги Рис.11 внутримкадный многоугольник @m, во втором – находим их пересечение. Вместо BufferWithCurves, понятно, можно использовать традиционныe STBuffer/BufferWithTolerance. Для наглядности в обоих случаях показана также сама МКАД в виде линии (@m.RingN(1)). В первом случае она окаймляет результат изнутри, во втором - снаружи.
select @m.RingN(1).STCurveToLine() union all select @m.RingN(1).BufferWithCurves(1000).STDifference(@m).STCurveToLine()
select @m.RingN(1).STCurveToLine() union all select @m.RingN(1).BufferWithCurves(1000).STIntersection(@m).STCurveToLine()
Рис.12
Для многоугольников, т.е. замкнутых контуров вместе с содержащей их областью, эпсилон может быть как положительным (в этом случае произойдет расширение фигуры), так и отрицательным (произойдет сужение).
--Расширяем Москву на километр за МКАД:
select @m.STBuffer(1000) union all select @m.RingN(1)
--Ужимаем Москву на километр внутрь МКАД:
select @m.STBuffer(-1000) union all select @m.RingN(1)
--То же для CURVEPOLYGON вместо POLYGON:
select @m.BufferWithCurves(1000).STCurveToLine()
select @m.BufferWithCurves(-1000).STCurveToLine()
Рис.13
Алексей Шуленин