Co to jest regresja?
Regresja działa przez ustanowienie relacji między zmiennymi w danych, które reprezentują charakterystykę — znaną jako cechy — obserwowanej rzeczy oraz zmienną, którą próbujemy przewidzieć — znaną jako etykieta.
Przypomnij sobie, że nasza firma wynajmuje rowery i chce przewidzieć oczekiwaną liczbę wypożyczeń w danym dniu. W takim przypadku funkcje obejmują takie rzeczy jak dzień tygodnia, miesiąc itd., a etykieta jest liczbą wypożyczeń rowerów.
Aby wytrenować model, zaczynamy od przykładu danych zawierającego funkcje, a także znanych wartości etykiety; w tym przypadku potrzebujemy danych historycznych, które obejmują daty, warunki pogodowe i liczbę wypożyczeń rowerów.
Następnie podzielimy te dane na dwa podzestawy:
- Zestaw danych treningowych , do którego zastosujemy algorytm określający funkcję hermetyzowaną relację między wartościami funkcji a znanymi wartościami etykiet.
- Zestaw danych weryfikacji lub testowania , którego możemy użyć do oceny modelu, używając go do generowania przewidywań etykiety i porównywania ich z rzeczywistymi znanymi wartościami etykiet.
Użycie danych historycznych ze znanymi wartościami etykiet do trenowania modelu sprawia, że regresja jest przykładem nadzorowanego uczenia maszynowego.
Prosty przykład
Przyjrzyjmy się prostemu przykładowi, aby zobaczyć, jak działa proces trenowania i oceny w zasadzie. Załóżmy, że upraszczamy scenariusz tak, abyśmy używali jednej funkcji — średniej temperatury dziennej — do przewidywania etykiety wypożyczania rowerów.
Zaczynamy od niektórych danych, które zawierają znane wartości funkcji średniej dziennej temperatury i etykiety wypożyczania rowerów.
| Temperatura | Wynajem |
|---|---|
| 56 | 210 |
| 61 | 126 |
| 67 | 137 |
| 72 | 140 |
| 76 | 152 |
| 82 | 156 |
| 54 | 114 |
| 62 | 129 |
Teraz losowo wybierzemy pięć z tych obserwacji i użyjemy ich do wytrenowania modelu regresji. Gdy mówimy o "trenowaniu modelu", oznacza to znalezienie funkcji (równanie matematyczne; nazwijmy to f), która może użyć funkcji temperatury (którą wywołamy x), aby obliczyć liczbę wypożyczeń (które wywołamy y). Innymi słowy, musimy zdefiniować następującą funkcję: f(x) = y.
Nasz zestaw danych szkoleniowych wygląda następująco:
| x | t |
|---|---|
| 56 | 210 |
| 61 | 126 |
| 67 | 137 |
| 72 | 140 |
| 76 | 152 |
Zacznijmy od wykreślenia wartości treningowych dla wartości x i y na wykresie:
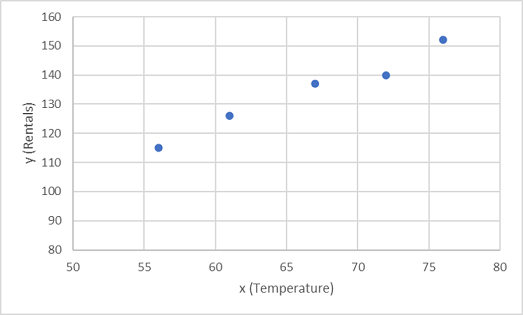
Teraz musimy dopasować te wartości do funkcji, co pozwala na losowe zmiany. Prawdopodobnie widać, że nakreślone punkty tworzą prawie prostą linię ukośną; innymi słowy, istnieje widoczna relacja liniowa między x i y, więc musimy znaleźć funkcję liniową, która jest najlepszym rozwiązaniem dla próbki danych. Istnieją różne algorytmy, których możemy użyć do określenia tej funkcji, która ostatecznie znajdzie prostą linię z minimalną ogólną wariancją od wykreślionych punktów; Jak to:
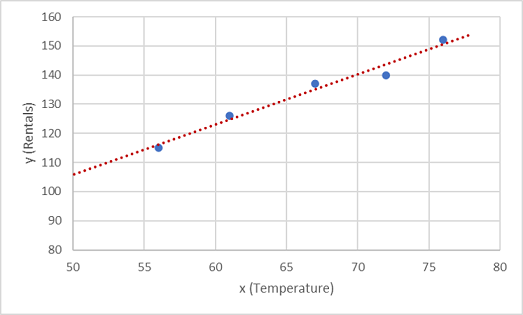
Linia reprezentuje funkcję liniową, która może być używana z dowolną wartością x w celu zastosowania nachylenia linii i jej przecięcia (gdzie linia przecina oś y, gdy x ma wartość 0), aby obliczyć y. W takim przypadku, jeśli przedłużyliśmy linię z lewej strony, okaże się, że gdy x wynosi 0, y wynosi około 20, a nachylenie linii jest takie, że dla każdej jednostki x przechodzisz wzdłuż po prawej stronie, y zwiększa się o około 1,7. W związku z tym możemy obliczyć naszą funkcję f jako 20 + 1,7x.
Teraz, gdy zdefiniowaliśmy naszą funkcję predykcyjną, możemy jej użyć do przewidywania etykiet dla danych walidacji, które wstrzymaliśmy i porównać przewidywane wartości (które zwykle wskazujemy za pomocą symbolu ŷ lub "y-hat") z rzeczywistymi znanymi wartościami y.
| x | t | ŷ |
|---|---|---|
| 82 | 156 | 159.4 |
| 54 | 114 | 111.8 |
| 62 | 129 | 125.4 |
Zobaczmy, jak wartości y i ŷ są porównywane na wykresie:
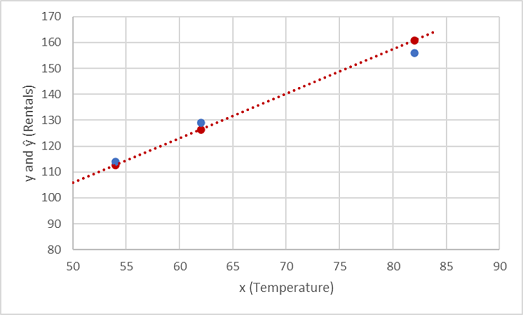
Wykreślone punkty, które znajdują się w wierszu funkcji, to przewidywane wartości ŷ obliczane przez funkcję, a pozostałe nakreślone punkty są rzeczywistymi wartościami y.
Istnieją różne sposoby mierzenia wariancji między przewidywanymi i rzeczywistymi wartościami. Możemy użyć tych metryk do oceny, jak dobrze przewiduje model.
Uwaga
Uczenie maszynowe opiera się na statystykach i matematyce i ważne jest, aby pamiętać o konkretnych terminach, których używają statystyk i matematycy (a tym samym analitycy danych). Możesz traktować różnicę między przewidywaną wartością etykiety a rzeczywistą wartością etykiety jako miarą błędu. Jednak w praktyce wartości "rzeczywiste" są oparte na przykładowych obserwacjach (które mogą podlegać pewnej losowej wariancji). Aby wyjaśnić, że porównujemy przewidywaną wartość (ŷ) z obserwowaną wartością (y), odnosimy się do różnicy między nimi jako reszt. Możemy podsumować reszty dla wszystkich przewidywań danych walidacji, aby obliczyć ogólną stratę w modelu jako miarę jego wydajności predykcyjnej.
Jednym z najczęstszych sposobów mierzenia straty jest kwadrat poszczególnych reszt, suma kwadratów i obliczenie średniej. Kwadratowanie reszt ma wpływ na oparcie obliczeń na wartościach bezwzględnych (ignorując, czy różnica jest ujemna, czy dodatnia) i dając większą wagę większym różnicom. Ta metryka jest nazywana błędem średniokwadratowym.
W przypadku naszych danych walidacji obliczenie wygląda następująco:
| t | ŷ | y — ŷ | (y — ŷ)2 |
|---|---|---|---|
| 156 | 159.4 | -3.4 | 11.56 |
| 114 | 111.8 | 2,2 | 4,84 |
| 129 | 125.4 | 3,6 | 12.96 |
| Sum | ∑ | 29.36 | |
| Średnia | x × | 9.79 |
W związku z tym utrata modelu oparta na metryce MSE wynosi 9,79.
Więc, czy to jest jakieś dobre? Trudno powiedzieć, ponieważ wartość MSE nie jest wyrażona w znaczącej jednostce miary. Wiemy, że im niższa jest wartość, tym mniejsza jest strata w modelu, a tym lepiej jest przewidywać. Dzięki temu przydatna jest metryka do porównywania dwóch modeli i znajdowania tego, który działa najlepiej.
Czasami bardziej przydatne jest wyrażenie utraty w tej samej jednostce miary co sama przewidywana wartość etykiety; w tym przypadku liczba wypożyczeń. Można to zrobić, obliczając pierwiastek kwadratowy MSE, który generuje metrykę znaną, zaskakująco, jako błąd średniokwadratowy (RMSE).
√9,79 = 3,13
Dlatego model RMSE wskazuje, że strata wynosi nieco ponad 3, co można zinterpretować luźno, co oznacza, że średnio nieprawidłowe przewidywania są błędne przez około trzech wypożyczeń.
Istnieje wiele innych metryk, których można użyć do mierzenia utraty w regresji. Na przykład R 2 (R-Squared) (czasami znany jako współczynnik determinacji) to korelacja między x a y kwadratem. Powoduje to wygenerowanie wartości z zakresu od 0 do 1, która mierzy ilość wariancji, którą można wyjaśnić przez model. Ogólnie rzecz biorąc, im bliżej ta wartość to 1, tym lepiej przewiduje model.