Ćwiczenie — wizualizowanie danych wyjściowych modelu

8 min

W tej lekcji zaimportujesz bibliotekę Matplotlib do notesu, z którym pracujesz, i skonfigurujesz ten notes pod kątem obsługi śródwierszowych danych wyjściowych biblioteki Matplotlib.

Przejdź z powrotem do notesu platformy Azure utworzonego w poprzedniej sekcji. Jeśli notes został zamknięty, możesz zalogować się z powrotem do portalu microsoft Azure Notebooks, otworzyć notes i użyć komórki ->Uruchom wszystko, aby ponownie uruchomić wszystkie komórki w notesie po jego otwarciu.
Wykonaj poniższe instrukcje w nowej komórce na końcu notesu. Zignoruj wszystkie komunikaty ostrzegawcze dotyczące buforowania czcionki:
```
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns

sns.set()
```
Pierwsza instrukcja jest jednym z kilku poleceń magic obsługiwanych przez jądro języka Python wybrane podczas tworzenia notesu. Umożliwia ono programowi Jupyter renderowanie danych wyjściowych biblioteki Matplotlib w notesie bez wykonywania wielokrotnych wywołań metody show. Należy je umieścić przed każdym odwołaniem do samej biblioteki Matplotlib. Ostatnia instrukcja konfiguruje bibliotekę Seaborn w celu poprawienia danych wyjściowych biblioteki Matplotlib.

Aby zobaczyć, jak działa biblioteka Matplotlib, wykonaj następujący kod w nowej komórce, aby wykreślić krzywą ROC dla modelu uczenia maszynowego utworzonego w poprzednim laboratorium:

from sklearn.metrics import roc_curve

fpr, tpr, _ = roc_curve(test_y, probabilities[:, 1])
plt.plot(fpr, tpr)
plt.plot([0, 1], [0, 1], color='grey', lw=1, linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')

Upewnij się, że zostały wyświetlone następujące dane wyjściowe:

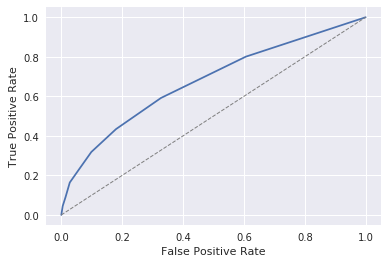
Krzywa ROC wygenerowana za pomocą biblioteki Matplotlib

Linia kropkowana w środku wykresu reprezentuje prawdopodobieństwo w stosunku 50-50 uzyskania poprawnej odpowiedzi. Niebieska krzywa reprezentuje dokładność modelu. Co ważniejsze, fakt, że ten wykres został w ogóle wyświetlony, pokazuje, że możesz używać biblioteki Matplotlib w notesie programu Jupyter.

Powodem, dla którego utworzyliśmy model uczenia maszynowego, jest przewidywanie, czy lot dotrze do celu na czas, czy z opóźnieniem. W tym ćwiczeniu napiszesz funkcję języka Python, która wywołuje model uczenia maszynowego utworzony w poprzednim laboratorium w celu obliczenia prawdopodobieństwa, że przylot będzie punktualny. Następnie użyjesz tej funkcji, aby przeanalizować kilka lotów.

Wprowadź poniższą definicję funkcji w nowej komórce, a następnie uruchom tę komórkę.

def predict_delay(departure_date_time, origin, destination):
    from datetime import datetime

    try:
        departure_date_time_parsed = datetime.strptime(departure_date_time, '%d/%m/%Y %H:%M:%S')
    except ValueError as e:
        return 'Error parsing date/time - {}'.format(e)

    month = departure_date_time_parsed.month
    day = departure_date_time_parsed.day
    day_of_week = departure_date_time_parsed.isoweekday()
    hour = departure_date_time_parsed.hour

    origin = origin.upper()
    destination = destination.upper()

    input = [{'MONTH': month,
              'DAY': day,
              'DAY_OF_WEEK': day_of_week,
              'CRS_DEP_TIME': hour,
              'ORIGIN_ATL': 1 if origin == 'ATL' else 0,
              'ORIGIN_DTW': 1 if origin == 'DTW' else 0,
              'ORIGIN_JFK': 1 if origin == 'JFK' else 0,
              'ORIGIN_MSP': 1 if origin == 'MSP' else 0,
              'ORIGIN_SEA': 1 if origin == 'SEA' else 0,
              'DEST_ATL': 1 if destination == 'ATL' else 0,
              'DEST_DTW': 1 if destination == 'DTW' else 0,
              'DEST_JFK': 1 if destination == 'JFK' else 0,
              'DEST_MSP': 1 if destination == 'MSP' else 0,
              'DEST_SEA': 1 if destination == 'SEA' else 0 }]

    return model.predict_proba(pd.DataFrame(input))[0][0]

Ta funkcja jako dane wejściowe przyjmuje datę i godzinę, kod lotniska początkowego oraz kod lotniska docelowego i zwraca wartość z zakresu od 0,0 do 1,0, wskazującą prawdopodobieństwo, że lot dotrze do miejsca docelowego na czas. W celu obliczenia prawdopodobieństwa używany jest model uczenia maszynowego utworzony w poprzednim laboratorium. Aby wywołać model, funkcja przekazuje obiekt DataFrame zawierający wartości wejściowe do funkcji predict_proba. Struktura tego obiektu DataFrame dokładnie odpowiada strukturze obiektu DataFrame, którego używaliśmy wcześniej.

Uwaga

Dane wejściowe daty funkcji predict_delay używają międzynarodowego formatu daty dd/mm/year.

Użyj poniższego kodu, aby obliczyć prawdopodobieństwo, że lot z Nowego Jorku do Atlanty wieczorem dnia 1 października dotrze na miejsce na czas. Wprowadzony rok nie ma znaczenia, ponieważ nie jest używany przez model.
```
predict_delay('1/10/2018 21:45:00', 'JFK', 'ATL')
```
Upewnij się, że dane wyjściowe pokazują, iż prawdopodobieństwo punktualnego przylotu wynosi 60%:

Przewidywanie, czy lot dotrze na czas
Zmodyfikuj kod, aby obliczyć prawdopodobieństwo, że ten sam lot dzień później dotrze na czas:
```
predict_delay('2/10/2018 21:45:00', 'JFK', 'ATL')
```
Jakie jest prawdopodobieństwo, że ten lot będzie punktualny? Gdyby Twoje plany podróży były elastyczne, czy warto by było rozważyć opóźnienie podróży o jeden dzień?
Teraz zmodyfikuj kod, aby obliczyć prawdopodobieństwo, że poranny lot tego samego dnia z Atlanty do Seattle przybędzie na czas:
```
predict_delay('2/10/2018 10:00:00', 'ATL', 'SEA')
```
Czy ten lot prawdopodobnie dotrze na czas?

Masz teraz prosty sposób na przewidzenie za pomocą jednego wiersza kodu, czy lot będzie prawdopodobnie punktualny, czy opóźniony. Możesz swobodnie poeksperymentować z innymi datami, godzinami, miejscami początkowymi i docelowymi. Pamiętaj jednak, że wyniki są znaczące tylko dla lotnisk o kodach ATL, DTW, JFK, MSP i SEA, ponieważ za pomocą tych kodów model został wytrenowany.

Wykonaj następujący kod, aby wykreślić prawdopodobieństwo punktualnego przylotu dla wieczornego lotu z lotniska JFK na lotnisko ATL dla pewnego zakresu dni:

import numpy as np

labels = ('Oct 1', 'Oct 2', 'Oct 3', 'Oct 4', 'Oct 5', 'Oct 6', 'Oct 7')
values = (predict_delay('1/10/2018 21:45:00', 'JFK', 'ATL'),
          predict_delay('2/10/2018 21:45:00', 'JFK', 'ATL'),
          predict_delay('3/10/2018 21:45:00', 'JFK', 'ATL'),
          predict_delay('4/10/2018 21:45:00', 'JFK', 'ATL'),
          predict_delay('5/10/2018 21:45:00', 'JFK', 'ATL'),
          predict_delay('6/10/2018 21:45:00', 'JFK', 'ATL'),
          predict_delay('7/10/2018 21:45:00', 'JFK', 'ATL'))
alabels = np.arange(len(labels))

plt.bar(alabels, values, align='center', alpha=0.5)
plt.xticks(alabels, labels)
plt.ylabel('Probability of On-Time Arrival')
plt.ylim((0.0, 1.0))

Sprawdź, czy dane wyjściowe wyglądają następująco:

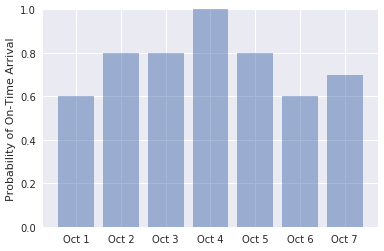
Prawdopodobieństwo punktualnych przylotów dla zakresu dat
Zmodyfikuj kod, aby wygenerować podobny wykres dla lotów opuszczających zestaw JFK dla MSP o godzinie 13:00 w dniu 10 kwietnia do 16 kwietnia. Jak wyglądają dane wyjściowe w porównaniu z poprzednimi danymi wyjściowymi?
Na własną rękę napisz kod, aby grafować prawdopodobieństwo, że loty opuszczające MORZE dla ATL o godzinie 9:00, południe, 15:00, 18:00, a 19:00 w dniu 30 stycznia przyjadą na czas. Upewnij się, że dane wyjściowe są zgodne z następującymi:

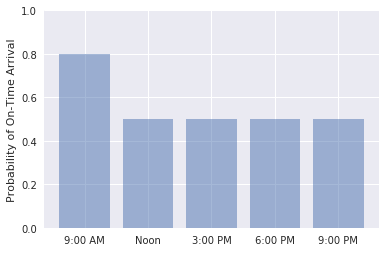
Prawdopodobieństwo punktualnych przylotów dla zakresu godzin

Jeśli dopiero zaczynasz pracę z biblioteką Matplotlib i chcesz dowiedzieć się więcej na jej temat, znajdziesz doskonały samouczek pod adresem https://www.labri.fr/perso/nrougier/teaching/matplotlib/. Biblioteka Matplotlib ma o wiele większe możliwości, niż pokazano tutaj — jest to jeden z powodów, dla których jest tak popularna w społeczności użytkowników języka Python.

Ćwiczenie — wizualizowanie danych wyjściowych modelu

Opinia