Porównanie i optymalizowanie krzywych ROC
Krzywe charakterystyczne operatora odbiornika (ROC) pozwalają porównać modele ze sobą i dostroić wybrany model. Omówimy, jak i dlaczego są one wykonywane.
Dostrajanie modelu
Najbardziej oczywistym zastosowaniem krzywej ROC jest wybranie progu decyzyjnego, który zapewnia najlepszą wydajność. Pamiętaj, że nasze modele zapewniają nam prawdopodobieństwo, takie jak 65% prawdopodobieństwo, że próbka jest podwyżką. Próg decyzyjny jest punktem powyżej, powyżej którego przypisano próbkę (turystę) lub poniżej przypisanej false (drzewa). Jeśli nasz próg decyzyjny wynosił 50%, wówczas 65% zostanie przydzielone do "true" (podwyżka). Jeśli jednak próg decyzyjny wynosił 70%, prawdopodobieństwo 65% byłoby zbyt małe i zostałoby przypisane do "false" (drzewo).
Widzieliśmy w poprzednim ćwiczeniu, że podczas konstruowania krzywej ROC po prostu zmieniamy próg decyzyjny i oceniamy, jak dobrze działa model. Gdy to zrobimy, możemy znaleźć próg, który daje optymalne wyniki.
Zwykle nie ma pojedynczego progu, który daje zarówno najlepszą wartość prawdziwie dodatnią (TPR), jak i niższą wartość fałszywie dodatnią (FPR). Oznacza to, że optymalny próg zależy od tego, co próbujesz osiągnąć. Na przykład w naszym scenariuszu bardzo ważne jest, aby mieć wysoki współczynnik prawdziwie dodatnich, ponieważ jeśli turysta nie zostanie zidentyfikowany i wystąpi lawina, zespół nie będzie wiedział, aby je uratować. Istnieje jednak kompromis: jeśli fałszywie dodatni wskaźnik jest zbyt wysoki, zespół ratowniczy może być wielokrotnie wysyłany do ratowania ludzi, którzy po prostu nie istnieją. W innych sytuacjach wskaźnik wyników fałszywie dodatnich jest uznawany za ważniejszy. Na przykład nauka ma niską tolerancję wyników fałszywie dodatnich. Gdyby fałszywie dodatni wskaźnik eksperymentów naukowych był wyższy, nie byłoby niekończącej się flurry sprzecznych twierdzeń i byłoby niemożliwe, aby zrozumieć, co jest prawdziwe.
Porównywanie modeli z usługą AUC
Za pomocą krzywych ROC można porównywać modele ze sobą, podobnie jak w przypadku funkcji kosztów. Krzywa ROC dla modelu pokazuje, jak dobrze będzie działać dla różnych progów decyzyjnych. Na koniec dnia najważniejsze jest to, jak będzie działać w świecie rzeczywistym, gdzie istnieje tylko jeden próg decyzyjny. Dlaczego więc chcemy porównać modele przy użyciu progów, których nigdy nie użyjemy? Istnieją dwie odpowiedzi na to.
Po pierwsze, porównanie krzywych ROC w określony sposób przypomina przeprowadzenie testu statystycznego, który informuje nas nie tylko, że jeden model lepiej radził sobie z tym konkretnym zestawem testowym, ale czy prawdopodobnie będzie nadal działać lepiej w przyszłości. Jest to poza zakresem tego materiału szkoleniowego, ale warto pamiętać.
Po drugie, krzywa ROC pokazuje, do pewnego stopnia, jak zależny jest od modelu na uzyskanie idealnego progu. Jeśli na przykład nasz model działa dobrze tylko wtedy, gdy mamy próg decyzyjny 0,9, ale strasznie powyżej lub poniżej tej wartości, nie jest to dobry projekt. Prawdopodobnie wolisz pracować z modelem, który działa rozsądnie dobrze dla różnych progów, wiedząc, że jeśli rzeczywiste dane, z którymi się spotykamy, różnią się nieco od naszego zestawu testowego, wydajność naszego modelu niekoniecznie się zwinie.
Jak porównać rocs?
Najprostszym sposobem porównywania liczbowych kontrolerów ROC jest użycie obszaru pod krzywą (AUC). Dosłownie jest to obszar grafu, który znajduje się poniżej krzywej. Na przykład nasz idealny model z ostatniego ćwiczenia ma wartość AUC 1:
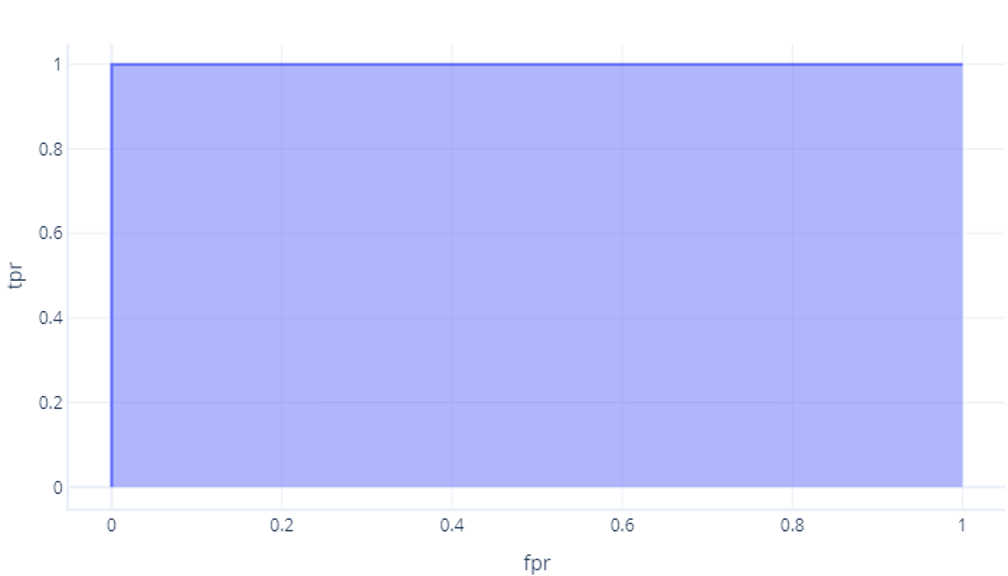
Chociaż nasz model, który nie był lepszy niż szansa, ma obszar około 0,5:
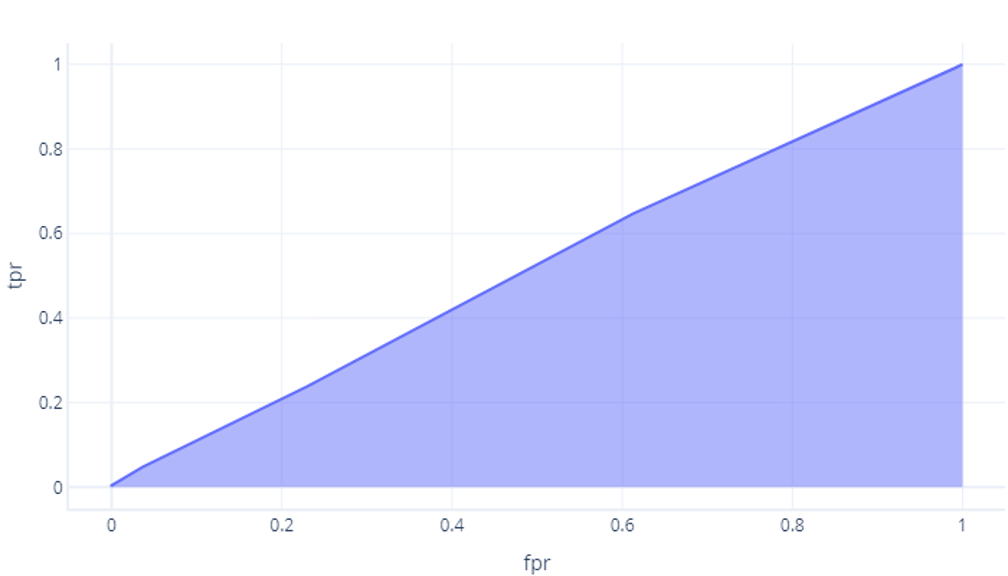
Tym bardziej idealny jest model, tym większy staje się ten obszar. Jeśli mamy model z dużą architekturą AUC, wiemy, że działa dobrze dla różnych progów, więc prawdopodobnie ma dobrą architekturę i został dobrze wytrenowany. Natomiast model z małą AUC (bliżej 0,5) nie działa dobrze.