Klasyfikacja wieloklasowa

  • 12 min

Klasyfikacja wieloklasowa służy do przewidywania, do której z wielu możliwych klas należy obserwacja. Jako nadzorowana technika uczenia maszynowego jest zgodna z tym samym trenowaniem iteracyjnym , weryfikowaniem i ocenianiem procesu jako regresji i klasyfikacji binarnej, w której podzbiór danych treningowych jest wstrzymany w celu zweryfikowania wytrenowanego modelu.

Przykład — klasyfikacja wieloklasowa

Algorytmy klasyfikacji wieloklasowej służą do obliczania wartości prawdopodobieństwa dla wielu etykiet klas, umożliwiając modelowi przewidywanie najbardziej prawdopodobnej klasy dla danej obserwacji.

Przyjrzyjmy się przykładowi, w którym mamy pewne obserwacje pingwinów, w których rejestrowana jest długość flippera (x) każdego pingwina. Dla każdej obserwacji dane obejmują gatunki pingwinów (y), które są kodowane w następujący sposób:

  • 0: Adelie
  • 1: Gentoo
  • 2: Chinstrap

Uwaga

Podobnie jak w przypadku poprzednich przykładów w tym module rzeczywisty scenariusz zawierałby wiele wartości funkcji (x). Użyjemy jednej funkcji, aby zachować prostotę.

Diagram of a measuring ruler. Diagram of three penguins.
Długość przerzucania (x) Gatunki (y)
167 0
172 0
225 2
197 1
189 1
232 2
158 0

Trenowanie modelu klasyfikacji wieloklasowej

Aby wytrenować model klasyfikacji wieloklasowej, musimy użyć algorytmu w celu dopasowania danych treningowych do funkcji, która oblicza wartość prawdopodobieństwa dla każdej możliwej klasy. Istnieją dwa rodzaje algorytmów, których można użyć, aby to zrobić:

  • Algorytmy OvR (One-vs-Rest)
  • Algorytmy wielomianowe

Algorytmy OvR (One-vs-Rest)

Algorytmy one-vs-REST trenują funkcję klasyfikacji binarnej dla każdej klasy, z których każda oblicza prawdopodobieństwo, że obserwacja jest przykładem klasy docelowej. Każda funkcja oblicza prawdopodobieństwo, że obserwacja jest określoną klasą w porównaniu z inną klasą. W przypadku naszego modelu klasyfikacji gatunków pingwinów algorytm zasadniczo tworzy trzy funkcje klasyfikacji binarnej:

  • f0(x) = P(y=0 | x)
  • f1(x) = P(y=1 | x)
  • f2(x) = P(y=2 | x)

Każdy algorytm tworzy funkcję sigmoid, która oblicza wartość prawdopodobieństwa z zakresu od 0,0 do 1,0. Model wyszkolony przy użyciu tego rodzaju algorytmu przewiduje klasę dla funkcji, która generuje najwyższe prawdopodobieństwo danych wyjściowych.

Algorytmy wielomianowe

Alternatywną metodą jest użycie algorytmu wielomianowego, który tworzy pojedynczą funkcję, która zwraca wielowarte dane wyjściowe. Dane wyjściowe to wektor (tablica wartości), który zawiera rozkład prawdopodobieństwa dla wszystkich możliwych klas — z wynikiem prawdopodobieństwa dla każdej klasy, który w przypadku sumy sumowanej do 1,0:

f(x) =[P(y=0|x), P(y=1|x), P(y=2|x)]

Przykładem tej funkcji jest funkcja softmax , która może wygenerować dane wyjściowe podobne do następującego przykładu:

[0.2, 0.3, 0.5]

Elementy w wektorze reprezentują prawdopodobieństwa dla klas 0, 1 i 2 odpowiednio; w tym przypadku klasa o najwyższym prawdopodobieństwie wynosi 2.

Niezależnie od tego, jakiego typu algorytm jest używany, model używa funkcji wynikowej do określenia najbardziej prawdopodobnej klasy dla danego zestawu funkcji (x) i przewiduje odpowiednią etykietę klasy (y).

Ocenianie modelu klasyfikacji wieloklasowej

Można ocenić klasyfikator wieloklasowy, obliczając metryki klasyfikacji binarnej dla każdej pojedynczej klasy. Alternatywnie można obliczyć zagregowane metryki, które uwzględniają wszystkie klasy.

Załóżmy, że zweryfikowaliśmy nasz klasyfikator wieloklasowy i uzyskaliśmy następujące wyniki:

Długość przerzucania (x) Rzeczywiste gatunki (y) Przewidywane gatunki (ŷ)
165 0 0
171 0 0
205 2 1
195 1 1
183 1 1
221 2 2
214 2 2

Macierz pomyłek dla klasyfikatora wieloklasowego jest podobna do klasyfikatora binarnego, z tą różnicą, że pokazuje liczbę przewidywań dla każdej kombinacji przewidywanych (ŷ) i rzeczywistych etykiet klas (y):

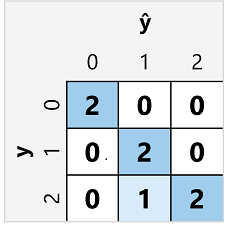
Diagram of a multiclass confusion matrix.

Z tej macierzy pomyłek możemy określić metryki dla każdej pojedynczej klasy w następujący sposób:

Klasa TP TN FP FN Dokładność Odwołaj Dokładność Wynik F1
0 2 5 0 0 1.0 1.0 1.0 1.0
1 2 4 1 0 0,86 1.0 0.67 0,8
2 2 4 0 1 0,86 0.67 1.0 0,8

Aby obliczyć ogólną dokładność, kompletność i precyzję metryk, należy użyć sumy metryk TP, TN, FP i FN :

  • Ogólna dokładność = (13+6)÷(13+6+1+1) = 0,90
  • Ogólna kompletność = 6÷(6+1) = 0,86
  • Ogólna precyzja = 6÷(6+1) = 0,86

Ogólny wynik F1 jest obliczany przy użyciu ogólnych metryk kompletności i dokładności:

  • Ogólny wynik F1 = (2x0,86x0,86)÷(0,86+0,86) = 0,86