Jak wysyłać informacje przy użyciu splątania?
W poprzednich lekcjach przedstawiono, że splątanie kwantowe może być doskonałym zasobem do komunikacji kwantowej. W tej lekcji zobaczysz jedną z najbardziej znanych aplikacji splątania: protokołu teleportacji kwantowej.
W teleportacji splątanie służy do transferu stanu kubitu z jednej lokalizacji do innej. Stan kubitu jest przenoszony do innego kubitu, ale sam kubit nie jest fizycznie przenoszony. Jest to ważna rzecz do zapamiętania! Informacje o stanie kubitu są przesyłane do innego kubitu, który jest używany jako statek do zapisywania informacji o kubitie komunikatu.
Protokół teleportacji używa kombinacji splątania i komunikacji klasycznej. Komunikacja klasyczna jest ważna, ponieważ protokół teleportacji wymaga od nadawcy przekazania wyników pomiarów do odbiornika. Oznacza to, że teleportacja nie może wysyłać informacji szybciej niż szybkość światła. Klasyczna komunikacja między nadawcą a odbiornikiem jest ograniczona przez szybkość światła.
Przejrzyjmy protokół teleportacji kwantowej.
Protokół teleportacji kwantowej
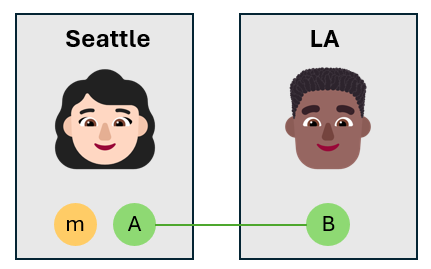
Alice i Bob współpracują ze sobą w tej samej firmie. Alice ma siedzibę w Seattle, a Bob ma siedzibę w Los Angeles. Pracują nad projektem, który wymaga od nich udostępniania informacji kwantowych. Decydują się na użycie teleportacji kwantowej do wysyłania między nimi informacji kwantowych.
Konfiguracja początkowa
Alice i Bob mają kubit, który jest częścią splątanej pary, która została wcześniej przygotowana. Splątana para jest stanem Bell, który jest stanem
$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B} + \ket{1_A 1_B})$$
Alicja ma dodatkowy kubit — nazywany kubitem komunikatu — i chce wysłać ten kubit do Boba. Kubit komunikatu jest w nieznanym stanie, który Alicja chce teleportować do Boba. Stan kubitu komunikatu to
$$\ket{m}=\alpha\ket{{0}_m + \beta\ket{{1}_m,$$
gdzie $\alpha$ i $\beta$ są liczbami zespolonymi.
Globalny stan Alicji i trzech kubitów Boba to
$$\ket{\text{Globalny}}= (\alpha\ket{{0}_m + \beta\ket{1}_m)\otimes\frac 1{\sqrt2}(\ket{0_A 0_B+ }1_A 1_B\ket{})$$
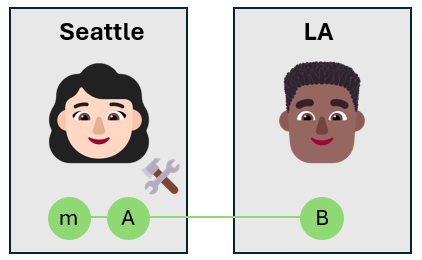
Alicja splątuje kubit wiadomości własnym kubitem
Alicja pobiera kubit komunikatu i spląta go własnym kubitem $A$ przy użyciu bramy CNOT. Kubit komunikatu jest kubitem sterującym, a kubit Alicji jest kubitem target . Spowoduje to utworzenie stanu splątania trzech kubitów.
Kubit komunikatu jest w nieznanym stanie $\alpha\ket{0}_m + \beta\ket{1}_m$, więc po zastosowaniu bramy CNOT kubity Alicji znajdują się w superpozycji czterech stanów Bell. Globalny stan trzech kubitów to
$$ \ket{\text{Globalny}}=\frac1{{2}\ket{\phi^+}_\text{mA} (\alpha\ket{{0}_B + _B) + \beta\ket{{1}$$
$$+ \frac1{{2}\ket{\phi^-}_\text{mA} (\alpha\ket{0}_B — \beta\ket{1}_B) +$$
$$+ \frac1{{2}\ket{\psi^+}_\text{mA}(\alpha\ket{1}_B + _B) + \beta\ket{0}$$
$$+ \frac1{{2}\ket{\psi^-}_\text{mA} (\alpha\ket{1}_B- \beta\ket{0}_B)$$
Globalny stan kubitów Alice i Boba to superpozycja czterech możliwych stanów.
Napiwek
Dobrym ćwiczeniem jest sprawdzenie, czy stan globalny trzech kubitów jest podany powyżej. Można to zrobić, stosując bramę CNOT do kubitu komunikatu i kubitu Alicji, a następnie rozwijając stan trzech kubitów.
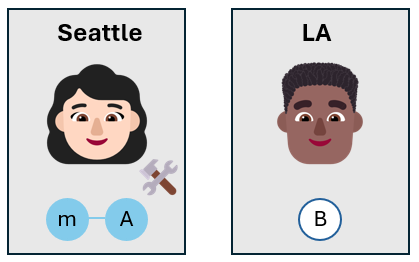
Alicja mierzy kubity
Alicja mierzy kubit komunikatu i jej własny kubit. Ona nie mierzy kubitów w $Z-basis$ jak zwykle, ale wybiera podstawę Bell. Podstawa Bell składa się z czterech stanów Bell, $\lbrace \ket{\phi^+}, \ket{\phi^-}, \ket{\psi^+}, \ket{\psi^-} \rbrace$.
Mierząc kubit komunikatu i jej własny kubit w bazie Bell, Alice projektuje swoje kubity w jeden z czterech stanów Bell. Ponieważ trzy kubity są splątane, wyniki pomiaru są skorelowane. Gdy Alicja mierzy swoje kubity, kubit Boba jest również przewidywany w skorelowanym stanie.
Jeśli na przykład Alicja mierzy jej kubity i obserwuje stan $\ket{\phi^-}$, kubit Boba jest przewidywany w stanie $\alpha\ket{0}_B — \beta\ket{1}_B$.
Alicja wywołuje Boba
Alicja dzwoni do Boba i mówi mu wyniki jej pomiarów. Używa klasycznego kanału komunikacyjnego, takiego jak rozmowa telefoniczna lub wiadomość SMS.
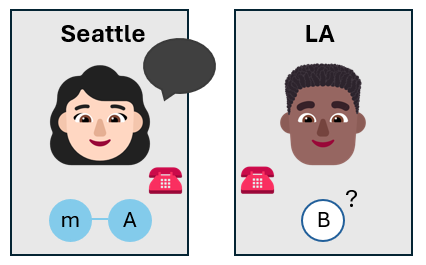
Bob zna teraz stan własnego kubitu, bez konieczności mierzenia go. Stan kubitu Boba może nie być taki sam jak stan kubitu komunikatu, który Alicja chciała teleportować, ale jest blisko niego.
Bob stosuje operację kwantową
Następnie Bob może odzyskać oryginalny stan kubitu komunikatu, stosując określoną operację kwantową do kubitu. Operacja Bob wykonuje zależy od tego, co Alice powiedział mu przez telefon.
Operacja, którą wykonuje, może być bramą Pauli $X$ , bramą Pauli $Z$ , zarówno, jak i żadnym.
Jeśli na przykład wynikiem pomiaru Alicji jest ^-, Bob wie, że jego kubit jest w stanie $\ket{\phi(}$$_B -\alpha\ket{0} _B)\beta.\ket{1}$ Musi tylko zastosować bramę Pauli Z, aby odzyskać oryginalny stan kubitu wiadomości.
| Miary Alicji | Bob stosuje |
|---|---|
| $\ket{\phi^+}$ | Brak operacji |
| $\ket{\phi^-}$ | Bramka Pauli Z |
| $\ket{\psi^+}$ | Bramka Pauli X |
| $\ket{\psi^-}$ | Bramka Pauli X, a następnie bramka Pauli Z |
Ta ostateczna operacja skutecznie teleportuje stan kubitu komunikatu na kubit Boba. Misja wykonana!
Ważne
Zastosowanie operacji do kubitu nie jest takie samo jak pomiar. Gdy Bob zastosuje operację, nie mierzy kubitu. Stosuje operację kwantową, która zmienia stan kubitu, ale nie zwija go.
W następnej lekcji zaimplementujesz protokół teleportacji kwantowej w programie Q#.