CompoundCurve
Dotyczy:SQL Server
Azure SQL Database
punkt końcowy analizy SQL w Microsoft Fabric
SQL Database w Microsoft Fabric
Warehouse w Microsoft Fabric
SQL Database w Microsoft Fabric
CompoundCurve to kolekcja zera lub więcej ciągłych wystąpień typu CircularString lub LineString, dla typów geometrii lub geografii.
Można utworzyć wystąpienie pustego CompoundCurve, ale aby CompoundCurve było prawidłowe, musi spełniać następujące warunki:
Musi zawierać co najmniej jedno wystąpienie CircularString lub LineString.
Sekwencja wystąpień CircularString lub LineString musi być ciągła.
Jeśli CompoundCurve zawiera sekwencję wielu CircularString i LineString, końcowy punkt dla każdego wystąpienia z wyjątkiem ostatniego musi być punktem początkowym dla następnego wystąpienia w sekwencji. Oznacza to, że jeśli punkt końcowy poprzedniego wystąpienia w sekwencji to (4 3 7 2), punkt początkowy dla następnego wystąpienia w sekwencji musi wynosić (4 3 7 2). Wartości Z(elevation) i M(measure) dla punktu również muszą być takie same. Jeśli istnieje różnica w dwóch punktach, zostanie zgłoszony System.FormatException. Punkty w CircularString nie muszą mieć wartości Z ani M. Jeśli dla punktu końcowego poprzedniego wystąpienia nie podano żadnych wartości Z lub M, punkt początkowy następnego wystąpienia nie może zawierać wartości Z lub M. Jeśli punkt końcowy dla poprzedniej sekwencji to (4 3), punkt początkowy następnej sekwencji musi wynosić (4 3); nie może być (4 3 7 2). Wszystkie punkty w wystąpieniu CompoundCurve muszą mieć albo brak wartości Z, albo tę samą wartość Z.
Instancje CompoundCurve
Poniższa ilustracja przedstawia poprawne typy CompoundCurve.
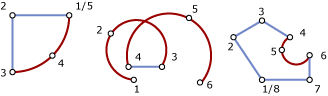
Zaakceptowane wystąpienia
CompoundCurve instancja jest akceptowana, jeśli jest pustą instancją lub spełnia następujące kryteria.
Wszystkie wystąpienia zawarte w wystąpieniu CompoundCurve są akceptowane jako wystąpienia segmentu łuku kołowego. Aby uzyskać więcej informacji na temat akceptowanych wystąpień segmentu łuku okręgowego, zobacz LineString i CircularString.
Wszystkie segmenty łuku cyklicznego w wystąpieniu CompoundCurve są połączone. Pierwszy punkt dla każdego następującego segmentu łuku cyklicznego jest taki sam jak ostatni punkt w poprzednim segmencie łuku cyklicznego.
Notatka
Obejmuje to współrzędne Z i M. Tak więc wszystkie cztery współrzędne X, Y, Z i M muszą być takie same.
Żadne z zawartych wystąpień nie są pustymi wystąpieniami.
W poniższym przykładzie przedstawiono zaakceptowane wystąpienia CompoundCurve.
DECLARE @g1 geometry = 'COMPOUNDCURVE EMPTY';
DECLARE @g2 geometry = 'COMPOUNDCURVE(CIRCULARSTRING(1 0, 0 1, -1 0), (-1 0, 2 0))';
Na poniższym przykładzie pokazano przypadki CompoundCurve, które nie są akceptowane. Te wystąpienia rzucają System.FormatException.
DECLARE @g1 geometry = 'COMPOUNDCURVE(CIRCULARSTRING EMPTY)';
DECLARE @g2 geometry = 'COMPOUNDCURVE(CIRCULARSTRING(1 0, 0 1, -1 0), (1 0, 2 0))';
Prawidłowe wystąpienia
Wystąpienie CompoundCurve jest prawidłowe, jeśli spełnia następujące kryteria.
Instancja CompoundCurve została zaakceptowana.
Wszystkie wystąpienia segmentu łuku okrągłego zawarte w wystąpieniu CompoundCurve są prawidłowymi wystąpieniami.
W poniższym przykładzie przedstawiono prawidłowe wystąpienia CompoundCurve.
DECLARE @g1 geometry = 'COMPOUNDCURVE EMPTY';
DECLARE @g2 geometry = 'COMPOUNDCURVE(CIRCULARSTRING(1 0, 0 1, -1 0), (-1 0, 2 0))';
DECLARE @g3 geometry = 'COMPOUNDCURVE(CIRCULARSTRING(1 1, 1 1, 1 1), (1 1, 3 5, 5 4))';
SELECT @g1.STIsValid(), @g2.STIsValid(), @g3.STIsValid();
@g3 jest prawidłowa, ponieważ instancja CircularString jest prawidłowa. Aby uzyskać więcej informacji na temat ważności wystąpienia CircularString, zobacz CircularString.
W poniższym przykładzie przedstawiono przypadki CompoundCurve, które są nieprawidłowe.
DECLARE @g1 geometry = 'COMPOUNDCURVE(CIRCULARSTRING(1 1, 1 1, 1 1), (1 1, 3 5, 5 4, 3 5))';
DECLARE @g2 geometry = 'COMPOUNDCURVE((1 1, 1 1))';
DECLARE @g3 geometry = 'COMPOUNDCURVE(CIRCULARSTRING(1 1, 2 3, 1 1))';
SELECT @g1.STIsValid(), @g2.STIsValid(), @g3.STIsValid();
@g1 jest nieprawidłowa, ponieważ drugie wystąpienie nie jest prawidłowym wystąpieniem LineString.
@g2 jest nieprawidłowa, ponieważ wystąpienie LineString jest nieprawidłowe.
@g3 nie jest prawidłowa, ponieważ instancja CircularString jest nieprawidłowa. Aby uzyskać więcej informacji na temat prawidłowych wystąpień CircularString i LineString, zobacz CircularString i LineString.
Przykłady
A. Utwórz instancję geometrii z pustą krzywą złożoną (CompoundCurve)
W poniższym przykładzie pokazano, jak utworzyć puste wystąpienie CompoundCurve:
DECLARE @g geometry;
SET @g = geometry::Parse('COMPOUNDCURVE EMPTY');
B. Deklarowanie i tworzenie wystąpienia geometrii przy użyciu klasy CompoundCurve w tej samej instrukcji
W poniższym przykładzie pokazano, jak zadeklarować i zainicjować wystąpienie geometry za pomocą CompoundCurvew tej samej instrukcji:
DECLARE @g geometry = 'COMPOUNDCURVE ((2 2, 0 0),CIRCULARSTRING (0 0, 1 2.1082, 3 6.3246, 0 7, -3 6.3246, -1 2.1082, 0 0))';
C. Utwórz instancję geograficzną z CompoundCurve
W poniższym przykładzie pokazano, jak zadeklarować i zainicjować instancję obszaru geograficznego przy użyciu CompoundCurve:
DECLARE @g geography = 'COMPOUNDCURVE(CIRCULARSTRING(-122.358 47.653, -122.348 47.649, -122.348 47.658, -122.358 47.658, -122.358 47.653))';
D. Przechowaj kwadrat w instancji CompoundCurve
W poniższym przykładzie użyto dwóch różnych sposobów użycia wystąpienia CompoundCurve do przechowywania kwadratu.
DECLARE @g1 geometry, @g2 geometry;
SET @g1 = geometry::Parse('COMPOUNDCURVE((1 1, 1 3), (1 3, 3 3),(3 3, 3 1), (3 1, 1 1))');
SET @g2 = geometry::Parse('COMPOUNDCURVE((1 1, 1 3, 3 3, 3 1, 1 1))');
SELECT @g1.STLength(), @g2.STLength();
Długości @g1 i @g2 są takie same. Zwróć uwagę na przykład, że wystąpienie CompoundCurve może przechowywać jedno lub więcej wystąpień LineString.
E. Utworzenie instancji geometrii przy użyciu CompoundCurve z wieloma CircularStrings
W poniższym przykładzie pokazano, jak za pomocą dwóch różnych wystąpień CircularString zainicjować CompoundCurve.
DECLARE @g geometry;
SET @g = geometry::Parse('COMPOUNDCURVE(CIRCULARSTRING(0 2, 2 0, 4 2), CIRCULARSTRING(4 2, 2 4, 0 2))');
SELECT @g.STLength();
Spowoduje to wygenerowanie wyniku 12.5663706143592, który jest równoważny 4pi. Wystąpienie CompoundCurve w przykładzie przechowuje okrąg z promieniem 2. Oba poprzednie przykłady kodu nie musiały używać CompoundCurve. W pierwszym przykładzie wystąpienie LineString byłoby prostsze, a wystąpienie CircularString byłoby prostsze w drugim przykładzie. Jednak w następnym przykładzie pokazano, gdzie CompoundCurve zapewnia lepszą alternatywę.
F. Użyj CompoundCurve do przechowywania półokręgu
W poniższym przykładzie użyto wystąpienia CompoundCurve do przechowywania półokręgu.
DECLARE @g geometry;
SET @g = geometry::Parse('COMPOUNDCURVE(CIRCULARSTRING(0 2, 2 0, 4 2), (4 2, 0 2))');
SELECT @g.STLength();
G. Przechowuj wiele wystąpień CircularString i LineString w obiekcie CompoundCurve
W poniższym przykładzie pokazano, jak można przechowywać wiele wystąpień CircularString i LineString przy użyciu CompoundCurve.
DECLARE @g geometry
SET @g = geometry::Parse('COMPOUNDCURVE((3 5, 3 3), CIRCULARSTRING(3 3, 5 1, 7 3), (7 3, 7 5), CIRCULARSTRING(7 5, 5 7, 3 5))');
SELECT @g.STLength();
H. Przechowywanie wystąpień z wartościami Z i M
W poniższym przykładzie pokazano, jak używać instancji CompoundCurve do przechowywania sekwencji instancji CircularString i LineString z wartościami Z i M.
SET @g = geometry::Parse('COMPOUNDCURVE(CIRCULARSTRING(7 5 4 2, 5 7 4 2, 3 5 4 2), (3 5 4 2, 8 7 4 2))');
I. Dlaczego wystąpienia usługi CircularString muszą być jawnie zadeklarowane
W poniższym przykładzie pokazano, dlaczego instancje CircularString muszą być jawnie zadeklarowane. Programista próbuje zapisać okrąg w instancji o nazwie CompoundCurve.
DECLARE @g1 geometry;
DECLARE @g2 geometry;
SET @g1 = geometry::Parse('COMPOUNDCURVE(CIRCULARSTRING(0 2, 2 0, 4 2), (4 2, 2 4, 0 2))');
SELECT 'Circle One', @g1.STLength() AS Perimeter; -- gives an inaccurate amount
SET @g2 = geometry::Parse('COMPOUNDCURVE(CIRCULARSTRING(0 2, 2 0, 4 2), CIRCULARSTRING(4 2, 2 4, 0 2))');
SELECT 'Circle Two', @g2.STLength() AS Perimeter; -- now we get an accurate amount
Oto zestaw wyników.
Circle One11.940039...
Circle Two12.566370...
Obwód Okręgu Dwa wynosi około 4π, co jest rzeczywistą długością obwodu. Jednak obwód circle one jest znacznie niedokładny. Wystąpienie Circle One CompoundCurve przechowuje jeden odcinek łuku (ABC) i dwa odcinki liniowe (CD, DA). Wystąpienie CompoundCurve musi przechowywać dwa cykliczne segmenty łuku (ABC, CDA) w celu zdefiniowania okręgu. Instancja LineString definiuje drugi zestaw punktów (4 2, 2 4, 0 2) w instancji CompoundCurve Kółka Pierwszego. Należy jawnie zadeklarować wystąpienie CircularString wewnątrz CompoundCurve.