Linie łamane i równania parametryczne
Użyj biblioteki SkiaSharp, aby renderować dowolną linię, którą można zdefiniować za pomocą równań parametrowych
W sekcji Krzywe i ścieżki SkiaSharp w tym przewodniku zobaczysz różne metody definiujące SKPath renderowanie niektórych typów krzywych. Jednak czasami konieczne jest rysowanie typu krzywej, która nie jest bezpośrednio obsługiwana przez SKPathelement . W takim przypadku można użyć wielolinii (kolekcji połączonych linii), aby narysować dowolną krzywą, którą można matematycznie zdefiniować. Jeśli utworzysz linie wystarczająco małe i wystarczająco liczne, wynik będzie wyglądać jak krzywa. Ta spirala jest rzeczywiście 3600 małych linii:

Ogólnie rzecz biorąc, najlepiej jest zdefiniować krzywą pod względem pary równań parametrycznych. Są to równania współrzędnych X i Y, które są zależne od trzeciej zmiennej, czasami wywoływane t na czas. Na przykład następujące równania parametryczne definiują okrąg z promieniem 1 wyśrodkowany w punkcie (0, 0) dla t z zakresu od 0 do 1:
x = cos(2πt)
y = sin(2πt)
Jeśli chcesz mieć promień większy niż 1, możesz po prostu pomnożyć sinus i wartości cosinus przez ten promień, a jeśli chcesz przenieść środek do innej lokalizacji, dodaj te wartości:
x = xCenter + radius·cos(2πt)
y = yCenter + radius·sin(2πt)
W przypadku wielokropka z osiami równoległymi do poziomego i pionowego są zaangażowane dwa promienie:
x = xCenter + xRadius·cos(2πt)
y = yCenter + yRadius·sin(2πt)
Następnie możesz umieścić odpowiedni kod SkiaSharp w pętli, która oblicza różne punkty i dodaje je do ścieżki. Poniższy kod SkiaSharp tworzy SKPath obiekt wielokropka, który wypełnia powierzchnię wyświetlania. Pętla przechodzi bezpośrednio przez 360 stopni. Środek jest połowę szerokości i wysokości powierzchni wyświetlacza, a więc są dwa promienie:
SKPath path = new SKPath();
for (float angle = 0; angle < 360; angle += 1)
{
double radians = Math.PI * angle / 180;
float x = info.Width / 2 + (info.Width / 2) * (float)Math.Cos(radians);
float y = info.Height / 2 + (info.Height / 2) * (float)Math.Sin(radians);
if (angle == 0)
{
path.MoveTo(x, y);
}
else
{
path.LineTo(x, y);
}
}
path.Close();
Powoduje to wielokropek zdefiniowany przez 360 małych linii. Gdy jest renderowany, wydaje się gładki.
Oczywiście nie trzeba tworzyć wielokropka przy użyciu wielolinii, ponieważ SKPath zawiera metodę AddOval , która ją wykonuje. Możesz jednak chcieć narysować obiekt wizualny, który nie jest dostarczany przez SKPathprogram .
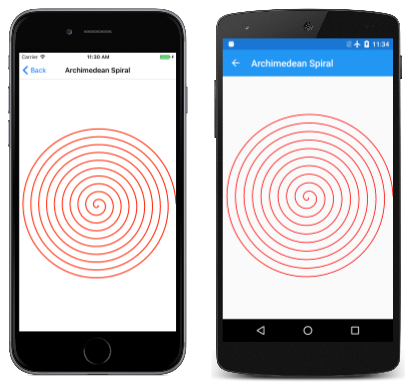
Strona Archimedean Spiral zawiera kod podobny do kodu wielokropka, ale z istotną różnicą. Pętle wokół 360 stopni okręgu 10 razy, stale dostosowując promień:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
SKPoint center = new SKPoint(info.Width / 2, info.Height / 2);
float radius = Math.Min(center.X, center.Y);
using (SKPath path = new SKPath())
{
for (float angle = 0; angle < 3600; angle += 1)
{
float scaledRadius = radius * angle / 3600;
double radians = Math.PI * angle / 180;
float x = center.X + scaledRadius * (float)Math.Cos(radians);
float y = center.Y + scaledRadius * (float)Math.Sin(radians);
SKPoint point = new SKPoint(x, y);
if (angle == 0)
{
path.MoveTo(point);
}
else
{
path.LineTo(point);
}
}
SKPaint paint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Red,
StrokeWidth = 5
};
canvas.DrawPath(path, paint);
}
}
Wynik jest również nazywany spiralą arytmetyczną, ponieważ przesunięcie między każdą pętlą jest stałe:
Zwróć uwagę, że element SKPath jest tworzony w using bloku. Zużywa to SKPath więcej pamięci niż SKPath obiekty w poprzednich programach, co sugeruje, że using blok jest bardziej odpowiedni do usuwania wszelkich niezarządzanych zasobów.