Trzy sposoby narysowania łuku

Dowiedz się, jak używać biblioteki SkiaSharp do definiowania łuków na trzy różne sposoby

Łuk jest krzywą na obwodzie wielokropka, takiego jak zaokrąglone części tego znaku nieskończoności:

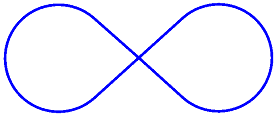
Pomimo prostoty tej definicji nie ma sposobu na zdefiniowanie funkcji rysowania łuku, która spełnia wszelkie potrzeby, a tym samym nie ma konsensusu między systemami graficznymi najlepszego sposobu rysowania łuku. Z tego powodu SKPath klasa nie ogranicza się tylko do jednego podejścia.

SKPath definiuje metodę AddArc , pięć różnych ArcTo metod i dwie metody względne RArcTo . Metody te dzielą się na trzy kategorie, reprezentując trzy bardzo różne podejścia do określania łuku. Który z nich jest używany, zależy od informacji dostępnych do zdefiniowania łuku i sposobu dopasowania tego łuku do innej grafiki, którą rysujesz.

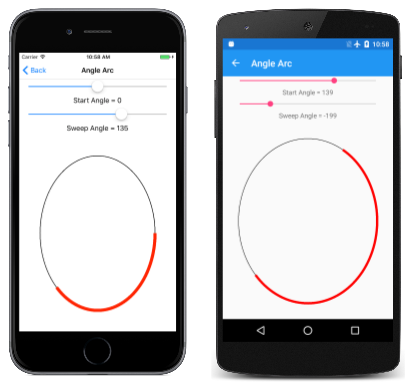
Łuk kątowy

Podejście łuku kątowego do rysowania łuków wymaga określenia prostokąta, który wiąże wielokropek. Łuk na obwodzie tego wielokropka jest wskazywany przez kąty od środka wielokropka, które wskazują początek łuku i jego długości. Dwie różne metody rysują łuki kątowe. AddArc Są to metoda i ArcTo metoda:

public void AddArc (SKRect oval, Single startAngle, Single sweepAngle)

public void ArcTo (SKRect oval, Single startAngle, Single sweepAngle, Boolean forceMoveTo)

Te metody są identyczne z metodami android AddArc i [ArcTo]xref:Android.Graphics.Path.ArcTo*). Metoda systemu iOS AddArc jest podobna, ale jest ograniczona do łuków na obwodzie okręgu, a nie uogólniony do wielokropka.

Obie metody zaczynają się od SKRect wartości, która definiuje zarówno lokalizację, jak i rozmiar wielokropka:

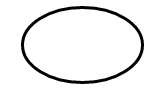
Łuk jest częścią obwodu tego wielokropka.

Argument startAngle jest kątem wskazówek zegara w stopniach względem linii poziomej pobranej od środka wielokropka po prawej stronie. Argument sweepAngle jest względny względem .startAngle Poniżej przedstawiono startAngle wartości sweepAngle 60 stopni i 100 stopni, odpowiednio:

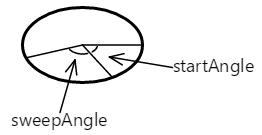
Łuk zaczyna się pod kątem początkowym. Jego długość podlega kątowi zamiatania. Łuk jest pokazany tutaj na czerwono:

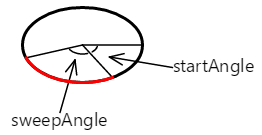
Krzywa dodana do ścieżki za pomocą AddArc metody or ArcTo jest po prostu tą częścią obwodu wielokropka:

startAngle Argumenty lub sweepAngle mogą być ujemne: Łuk jest zgodnie z ruchem wskazówek zegara dla wartości dodatnich sweepAngle i odwrotnie zgodnie z ruchem wskazówek zegara dla wartości ujemnych.

AddArc Nie definiuje jednak zamkniętego konturu. Jeśli wywołasz LineTo metodę po AddArcmetodzie , wiersz jest rysowany od końca łuku do punktu w metodzie LineTo , a to samo dotyczy ArcTowartości .

AddArc automatycznie uruchamia nowy kontur i funkcjonalnie odpowiada wywołaniu ArcTo funkcji z ostatnim argumentem true:

path.ArcTo (oval, startAngle, sweepAngle, true);

Ten ostatni argument jest nazywany forceMoveTo, i skutecznie powoduje MoveTo wywołanie na początku łuku. To zaczyna nowy kontur. Tak nie jest w przypadku ostatniego argumentu :false

path.ArcTo (oval, startAngle, sweepAngle, false);

Ta wersja ArcTo rysuje linię z bieżącej pozycji na początek łuku. Oznacza to, że łuk może znajdować się w środku większego konturu.

Strona Kąt łuku umożliwia określenie kątów rozpoczęcia i zamiatania za pomocą dwóch suwaków. Plik XAML tworzy wystąpienie dwóch Slider elementów i .SKCanvasView Procedura PaintCanvas obsługi w pliku AngleArcPage.xaml.cs rysuje zarówno owalny, jak i łuk przy użyciu dwóch SKPaint obiektów zdefiniowanych jako pola:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    SKRect rect = new SKRect(100, 100, info.Width - 100, info.Height - 100);
    float startAngle = (float)startAngleSlider.Value;
    float sweepAngle = (float)sweepAngleSlider.Value;

    canvas.DrawOval(rect, outlinePaint);

    using (SKPath path = new SKPath())
    {
        path.AddArc(rect, startAngle, sweepAngle);
        canvas.DrawPath(path, arcPaint);
    }
}

Jak widać, zarówno kąt rozpoczęcia, jak i kąt zamiatania mogą przyjmować wartości ujemne:

Takie podejście do generowania łuku jest algorytmicznie najprostsze i łatwo jest uzyskać równania parametryczne, które opisują łuk. Znajomość rozmiaru i lokalizacji wielokropka oraz kątów rozpoczęcia i zamiatania można obliczyć punkty początkowe i końcowe łuku przy użyciu prostej trygonometrii:

x = oval.MidX + (oval.Width / 2) * cos(angle)

y = oval.MidY + (oval.Height / 2) * sin(angle)

Wartość angle to startAngle lub startAngle + sweepAngle.

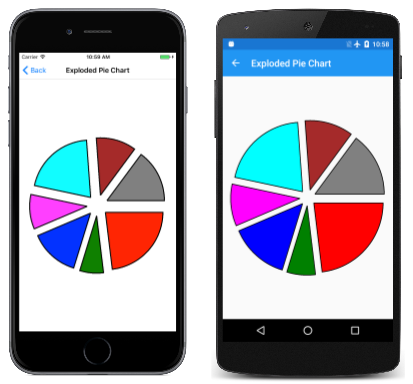
Użycie dwóch kątów do zdefiniowania łuku jest najlepsze w przypadkach, w których znasz długość kątową łuku, który ma zostać narysowy, na przykład w celu utworzenia wykresu kołowego. Na stronie Eksplodowany wykres kołowy pokazano to. Klasa ExplodedPieChartPage używa klasy wewnętrznej do definiowania niektórych s szkieletowanych danych i kolorów:

class ChartData
{
    public ChartData(int value, SKColor color)
    {
        Value = value;
        Color = color;
    }

    public int Value { private set; get; }

    public SKColor Color { private set; get; }
}

ChartData[] chartData =
{
    new ChartData(45, SKColors.Red),
    new ChartData(13, SKColors.Green),
    new ChartData(27, SKColors.Blue),
    new ChartData(19, SKColors.Magenta),
    new ChartData(40, SKColors.Cyan),
    new ChartData(22, SKColors.Brown),
    new ChartData(29, SKColors.Gray)
};

Procedura PaintSurface obsługi najpierw przechodzi przez elementy, aby obliczyć totalValues liczbę. W tym celu może określić rozmiar każdego elementu jako ułamek sumy i przekonwertować go na kąt:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    int totalValues = 0;

    foreach (ChartData item in chartData)
    {
        totalValues += item.Value;
    }

    SKPoint center = new SKPoint(info.Width / 2, info.Height / 2);
    float explodeOffset = 50;
    float radius = Math.Min(info.Width / 2, info.Height / 2) - 2 * explodeOffset;
    SKRect rect = new SKRect(center.X - radius, center.Y - radius,
                             center.X + radius, center.Y + radius);

    float startAngle = 0;

    foreach (ChartData item in chartData)
    {
        float sweepAngle = 360f * item.Value / totalValues;

        using (SKPath path = new SKPath())
        using (SKPaint fillPaint = new SKPaint())
        using (SKPaint outlinePaint = new SKPaint())
        {
            path.MoveTo(center);
            path.ArcTo(rect, startAngle, sweepAngle, false);
            path.Close();

            fillPaint.Style = SKPaintStyle.Fill;
            fillPaint.Color = item.Color;

            outlinePaint.Style = SKPaintStyle.Stroke;
            outlinePaint.StrokeWidth = 5;
            outlinePaint.Color = SKColors.Black;

            // Calculate "explode" transform
            float angle = startAngle + 0.5f * sweepAngle;
            float x = explodeOffset * (float)Math.Cos(Math.PI * angle / 180);
            float y = explodeOffset * (float)Math.Sin(Math.PI * angle / 180);

            canvas.Save();
            canvas.Translate(x, y);

            // Fill and stroke the path
            canvas.DrawPath(path, fillPaint);
            canvas.DrawPath(path, outlinePaint);
            canvas.Restore();
        }

        startAngle += sweepAngle;
    }
}

Dla każdego wycinka kołowego jest tworzony nowy SKPath obiekt. Ścieżka składa się z linii z środka, a następnie ArcTo do rysowania łuku i innej linii z powrotem do środka wyników wywołania Close . Ten program wyświetla wycinki kołowe "eksplodowane", przenosząc je wszystkie z środka o 50 pikseli. To zadanie wymaga wektora w kierunku środkowego kąta zamiatania dla każdego wycinka:

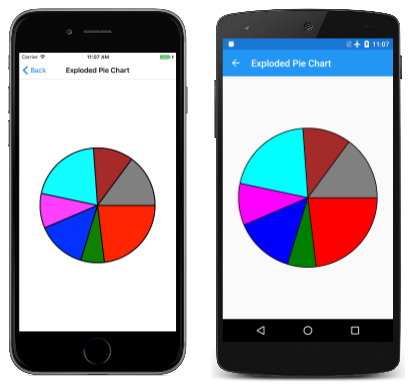
Aby zobaczyć, jak to wygląda bez "eksplozji", po prostu skomentuj Translate połączenie:

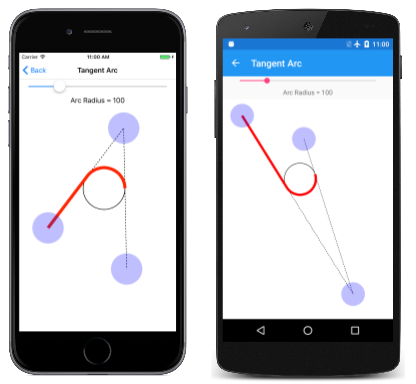
Łuk tangensowy

Drugim typem łuku obsługiwanego przez SKPath jest łuk tangensowy, tak zwany, ponieważ łuk jest obwodem okręgu, który jest tangensem do dwóch połączonych linii.

Łuk tangensowy jest dodawany do ścieżki z wywołaniem ArcTo metody z dwoma SKPoint parametrami lub ArcTo przeciążeniem z oddzielnymi Single parametrami dla punktów:

public void ArcTo (SKPoint point1, SKPoint point2, Single radius)

public void ArcTo (Single x1, Single y1, Single x2, Single y2, Single radius)

Ta ArcTo metoda jest podobna do funkcji PostScript arct (page 532) i metody systemu iOS AddArcToPoint .

Metoda ArcTo obejmuje trzy punkty:

• Bieżący punkt konturu lub punkt (0, 0), jeśli MoveTo nie został wywołany
• Pierwszy argument punktu do ArcTo metody, nazywany punktem narożnym
• Drugi argument punktu na ArcTo, nazywany punktem docelowym:

Te trzy punkty definiują dwa połączone linie:

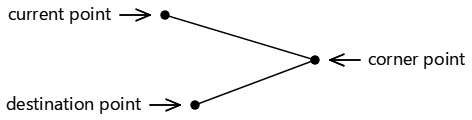
Jeśli trzy punkty są grube — to znaczy, jeśli leżą na tej samej prostej linii — żaden łuk nie zostanie narysowany.

Metoda ArcTo zawiera radius również parametr. Definiuje promień okręgu:

Łuk tangensowy nie jest uogólniony dla wielokropka.

Jeśli dwa linie spełniają dowolny kąt, można wstawić ten okrąg między tymi liniami, tak aby był styczny dla obu linii:

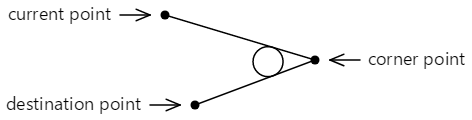
Krzywa dodawana do konturu nie dotyka żadnego z punktów określonych w metodzie ArcTo . Składa się z prostej linii od bieżącego punktu do pierwszego punktu tangensowego i łuku kończącego się w drugim punkcie tangensowym, pokazanym tutaj na czerwono:

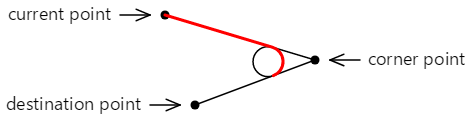
Oto ostatnia linia prosta i łuk dodany do konturu:

Kontur może być kontynuowany z drugiego punktu tangensowego.

Strona Tangent Arc umożliwia eksperymentowanie z łukiem tangensowym. Jest to pierwsza z kilku stron, które pochodzą z InteractivePageklasy , która definiuje kilka przydatnych SKPaint obiektów i wykonuje TouchPoint przetwarzanie:

public class InteractivePage : ContentPage
{
    protected SKCanvasView baseCanvasView;
    protected TouchPoint[] touchPoints;

    protected SKPaint strokePaint = new SKPaint
    {
        Style = SKPaintStyle.Stroke,
        Color = SKColors.Black,
        StrokeWidth = 3
    };

    protected SKPaint redStrokePaint = new SKPaint
    {
        Style = SKPaintStyle.Stroke,
        Color = SKColors.Red,
        StrokeWidth = 15
    };

    protected SKPaint dottedStrokePaint = new SKPaint
    {
        Style = SKPaintStyle.Stroke,
        Color = SKColors.Black,
        StrokeWidth = 3,
        PathEffect = SKPathEffect.CreateDash(new float[] { 7, 7 }, 0)
    };

    protected void OnTouchEffectAction(object sender, TouchActionEventArgs args)
    {
        bool touchPointMoved = false;

        foreach (TouchPoint touchPoint in touchPoints)
        {
            float scale = baseCanvasView.CanvasSize.Width / (float)baseCanvasView.Width;
            SKPoint point = new SKPoint(scale * (float)args.Location.X,
                                        scale * (float)args.Location.Y);
            touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
        }

        if (touchPointMoved)
        {
            baseCanvasView.InvalidateSurface();
        }
    }
}

Klasa TangentArcPage pochodzi z klasy InteractivePage. Konstruktor w pliku TangentArcPage.xaml.cs jest odpowiedzialny za utworzenie wystąpienia i zainicjowanie touchPoints tablicy oraz ustawienie baseCanvasView (w pliku InteractivePage) do SKCanvasView obiektu utworzonego w pliku TangentArcPage.xaml:

public partial class TangentArcPage : InteractivePage
{
    public TangentArcPage()
    {
        touchPoints = new TouchPoint[3];

        for (int i = 0; i < 3; i++)
        {
            TouchPoint touchPoint = new TouchPoint
            {
                Center = new SKPoint(i == 0 ? 100 : 500,
                                     i != 2 ? 100 : 500)
            };
            touchPoints[i] = touchPoint;
        }

        InitializeComponent();

        baseCanvasView = canvasView;
        radiusSlider.Value = 100;
    }

    void sliderValueChanged(object sender, ValueChangedEventArgs args)
    {
        if (canvasView != null)
        {
            canvasView.InvalidateSurface();
        }
    }
    ...
}

Procedura PaintSurface obsługi używa ArcTo metody do rysowania łuku na podstawie punktów dotykowych i Slider, ale także algorytmicznie oblicza okrąg, na podstawie którego jest kąt:

public partial class TangentArcPage : InteractivePage
{
    ...
    void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
    {
        SKImageInfo info = args.Info;
        SKSurface surface = args.Surface;
        SKCanvas canvas = surface.Canvas;

        canvas.Clear();

        // Draw the two lines that meet at an angle
        using (SKPath path = new SKPath())
        {
            path.MoveTo(touchPoints[0].Center);
            path.LineTo(touchPoints[1].Center);
            path.LineTo(touchPoints[2].Center);
            canvas.DrawPath(path, dottedStrokePaint);
        }

        // Draw the circle that the arc wraps around
        float radius = (float)radiusSlider.Value;

        SKPoint v1 = Normalize(touchPoints[0].Center - touchPoints[1].Center);
        SKPoint v2 = Normalize(touchPoints[2].Center - touchPoints[1].Center);

        double dotProduct = v1.X * v2.X + v1.Y * v2.Y;
        double angleBetween = Math.Acos(dotProduct);
        float hypotenuse = radius / (float)Math.Sin(angleBetween / 2);
        SKPoint vMid = Normalize(new SKPoint((v1.X + v2.X) / 2, (v1.Y + v2.Y) / 2));
        SKPoint center = new SKPoint(touchPoints[1].Center.X + vMid.X * hypotenuse,
                                     touchPoints[1].Center.Y + vMid.Y * hypotenuse);

        canvas.DrawCircle(center.X, center.Y, radius, this.strokePaint);

        // Draw the tangent arc
        using (SKPath path = new SKPath())
        {
            path.MoveTo(touchPoints[0].Center);
            path.ArcTo(touchPoints[1].Center, touchPoints[2].Center, radius);
            canvas.DrawPath(path, redStrokePaint);
        }

        foreach (TouchPoint touchPoint in touchPoints)
        {
            touchPoint.Paint(canvas);
        }
    }

    // Vector methods
    SKPoint Normalize(SKPoint v)
    {
        float magnitude = Magnitude(v);
        return new SKPoint(v.X / magnitude, v.Y / magnitude);
    }

    float Magnitude(SKPoint v)
    {
        return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);
    }
}

Oto strona Tangent Arc uruchomiona:

Łuk tangensowy jest idealny do tworzenia zaokrąglonych narożników, takich jak zaokrąglony prostokąt. Ponieważ SKPath już zawiera metodęAddRoundedRect, strona Zaokrąglona heptagon pokazuje, jak używać ArcTo do zaokrąglania narożników siedmiostronnego wielokąta. (Kod jest uogólniony dla każdego zwykłego wielokąta).

Procedura PaintSurface obsługi RoundedHeptagonPage klasy zawiera jedną for pętlę do obliczenia współrzędnych siedmiu wierzchołków szepta, a drugi do obliczenia punktów środkowych siedmiu stron z tych wierzchołków. Te punkty środkowe są następnie używane do konstruowania ścieżki:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    float cornerRadius = 100;
    int numVertices = 7;
    float radius = 0.45f * Math.Min(info.Width, info.Height);

    SKPoint[] vertices = new SKPoint[numVertices];
    SKPoint[] midPoints = new SKPoint[numVertices];

    double vertexAngle = -0.5f * Math.PI;       // straight up

    // Coordinates of the vertices of the polygon
    for (int vertex = 0; vertex < numVertices; vertex++)
    {
        vertices[vertex] = new SKPoint(radius * (float)Math.Cos(vertexAngle),
                                       radius * (float)Math.Sin(vertexAngle));
        vertexAngle += 2 * Math.PI / numVertices;
    }

    // Coordinates of the midpoints of the sides connecting the vertices
    for (int vertex = 0; vertex < numVertices; vertex++)
    {
        int prevVertex = (vertex + numVertices - 1) % numVertices;
        midPoints[vertex] = new SKPoint((vertices[prevVertex].X + vertices[vertex].X) / 2,
                                        (vertices[prevVertex].Y + vertices[vertex].Y) / 2);
    }

    // Create the path
    using (SKPath path = new SKPath())
    {
        // Begin at the first midpoint
        path.MoveTo(midPoints[0]);

        for (int vertex = 0; vertex < numVertices; vertex++)
        {
            SKPoint nextMidPoint = midPoints[(vertex + 1) % numVertices];

            // Draws a line from the current point, and then the arc
            path.ArcTo(vertices[vertex], nextMidPoint, cornerRadius);

            // Connect the arc with the next midpoint
            path.LineTo(nextMidPoint);
        }
        path.Close();

        // Render the path in the center of the screen
        using (SKPaint paint = new SKPaint())
        {
            paint.Style = SKPaintStyle.Stroke;
            paint.Color = SKColors.Blue;
            paint.StrokeWidth = 10;

            canvas.Translate(info.Width / 2, info.Height / 2);
            canvas.DrawPath(path, paint);
        }
    }
}

Oto uruchomiony program:

Łuk wielokropowy

Wielokropek jest dodawany do ścieżki z wywołaniem ArcTo metody, która ma dwa SKPoint parametry, lub ArcTo przeciążenie z oddzielnymi współrzędnymi X i Y:

public void ArcTo (SKPoint r, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, SKPoint xy)

public void ArcTo (Single rx, Single ry, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, Single x, Single y)

Łuk wielokropowy jest zgodny z wielokropkiem zawartym w skalowalnej grafice wektorowej (SVG) i klasy platforma uniwersalna systemu WindowsArcSegment.

Metody te ArcTo narysują łuk między dwoma punktami, które są bieżącym punktem konturu, a ostatnim parametrem metody (xyparametrem ArcTo lub oddzielnymi x parametrami iy):

Pierwszy parametr punktu do ArcTo metody (rlub rx i ry) nie jest punktem w ogóle, ale zamiast tego określa poziome i pionowe promienie wielokropka;

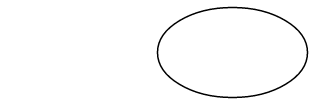
Parametr xAxisRotate jest liczbą stopni zegara, aby obrócić ten wielokropek:

Jeśli ten pochylony wielokropek jest następnie umieszczony tak, aby dotykał dwóch punktów, punkty są połączone przez dwa różne łuki:

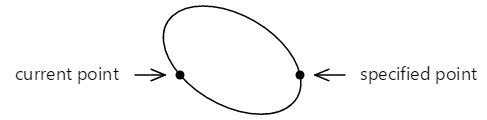
Te dwa łuki można odróżnić na dwa sposoby: Górny łuk jest większy niż dolny łuk, a łuk jest rysowany od lewej do prawej, górny łuk jest rysowany w kierunku wskazówek zegara, podczas gdy dolny łuk jest rysowany w kierunku przeciwdłodobowym.

Istnieje również możliwość dopasowania wielokropka między dwoma punktami w inny sposób:

Teraz jest mniejszy łuk na górze, który jest rysowany zgodnie z ruchem wskazówek zegara, a większy łuk na dole, który jest rysowany w kierunku wskazówek zegara.

W związku z tym te dwa punkty mogą być połączone łukiem zdefiniowanym przez wielokropek pochylony na cztery sposoby:

Te cztery łuki są rozróżniane przez cztery kombinacje argumentów SKPathArcSize typu i SKPathDirection wyliczenia do ArcTo metody :

• czerwony: SKPathArcSize.Large i SKPathDirection.Clockwise
• zielony: SKPathArcSize.Small i SKPathDirection.Clockwise
• niebieski: SKPathArcSize.Small i SKPathDirection.CounterClockwise
• magenta: SKPathArcSize.Large i SKPathDirection.CounterClockwise

Jeśli pochylony wielokropek nie jest wystarczająco duży, aby zmieścić się między dwoma punktami, to jest równomiernie skalowany, dopóki nie będzie wystarczająco duży. Tylko dwa unikatowe łuki łączą dwa punkty w tym przypadku. Można je odróżnić za pomocą parametru SKPathDirection .

Chociaż takie podejście do definiowania łuku wydaje się złożone w pierwszym spotkaniu, jest to jedyne podejście, które umożliwia definiowanie łuku z obróconą wielokropkiem i często jest to najprostsze podejście, gdy trzeba zintegrować łuki z innymi częściami konturu.

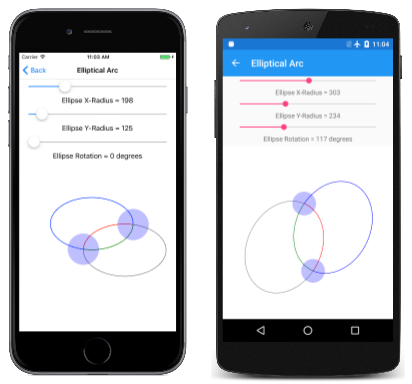
Strona Łuk wielokropka umożliwia interaktywne ustawianie dwóch punktów oraz rozmiaru i obrotu wielokropka. Klasa EllipticalArcPage pochodzi z InteractivePageklasy , a PaintSurface program obsługi w pliku EllipticalArcPage.xaml.cs code-behind pobiera cztery łuki:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    using (SKPath path = new SKPath())
    {
        int colorIndex = 0;
        SKPoint ellipseSize = new SKPoint((float)xRadiusSlider.Value,
                                          (float)yRadiusSlider.Value);
        float rotation = (float)rotationSlider.Value;

        foreach (SKPathArcSize arcSize in Enum.GetValues(typeof(SKPathArcSize)))
            foreach (SKPathDirection direction in Enum.GetValues(typeof(SKPathDirection)))
            {
                path.MoveTo(touchPoints[0].Center);
                path.ArcTo(ellipseSize, rotation,
                           arcSize, direction,
                           touchPoints[1].Center);

                strokePaint.Color = colors[colorIndex++];
                canvas.DrawPath(path, strokePaint);
                path.Reset();
            }
    }

    foreach (TouchPoint touchPoint in touchPoints)
    {
        touchPoint.Paint(canvas);
    }
}

W tym miejscu działa:

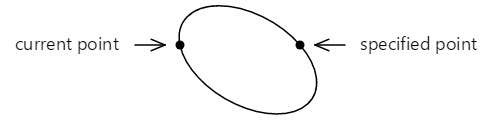
Strona Nieskończoność Łuku używa łuku wielokropkowego, aby narysować znak nieskończoności. Znak nieskończoności opiera się na dwóch okręgach z promieniami 100 jednostek oddzielonych 100 jednostkami:

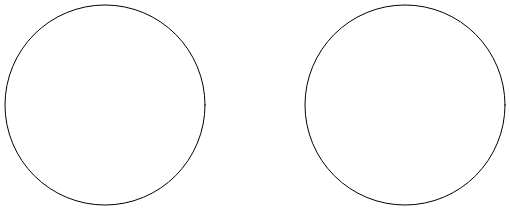
Dwa linie przecinające się między sobą są tangensem dla obu okręgów:

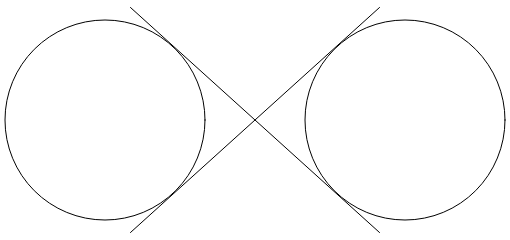
Znak nieskończoności jest kombinacją części tych okręgów i dwóch linii. Aby użyć łuku wielokropkowego, aby narysować znak nieskończoności, współrzędne, w których dwa linie są tangensem okręgów, muszą być określone.

Konstruowanie prawego prostokąta w jednym z okręgów:

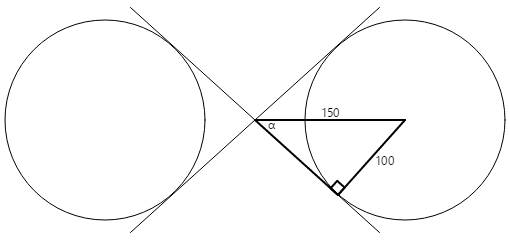
Promień okręgu wynosi 100 jednostek, a niedociągnienie trójkąta wynosi 150 jednostek, więc kąt α jest arcusinus (odwrotny sinus) 100 podzielony przez 150 lub 41,8 stopni. Długość drugiej strony trójkąta wynosi 150 razy cosinus 41,8 stopni lub 112, które można również obliczyć przez twierdzenie Pythagorean.

Współrzędne punktu tangensa można następnie obliczyć przy użyciu tych informacji:

x = 112·cos(41.8) = 83

y = 112·sin(41.8) = 75

Cztery punkty tangensowe są niezbędne do narysowania znaku nieskończoności wyśrodkowanego w punkcie (0, 0) z promieniem okręgu 100:

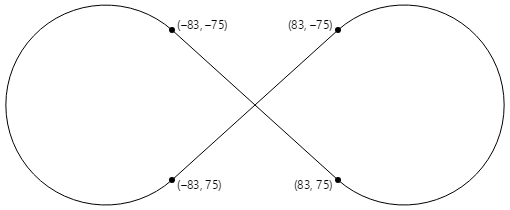
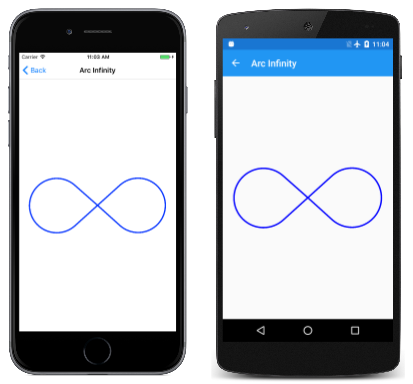
Procedura PaintSurface obsługi w ArcInfinityPage klasie umieszcza znak nieskończoności, tak aby punkt (0, 0) był umieszczony w środku strony i skaluje ścieżkę do rozmiaru ekranu:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    using (SKPath path = new SKPath())
    {
        path.LineTo(83, 75);
        path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.CounterClockwise, 83, -75);
        path.LineTo(-83, 75);
        path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.Clockwise, -83, -75);
        path.Close();

        // Use path.TightBounds for coordinates without control points
        SKRect pathBounds = path.Bounds;

        canvas.Translate(info.Width / 2, info.Height / 2);
        canvas.Scale(Math.Min(info.Width / pathBounds.Width,
                              info.Height / pathBounds.Height));

        using (SKPaint paint = new SKPaint())
        {
            paint.Style = SKPaintStyle.Stroke;
            paint.Color = SKColors.Blue;
            paint.StrokeWidth = 5;

            canvas.DrawPath(path, paint);
        }
    }
}

Kod używa Bounds właściwości , SKPath aby określić wymiary sinusu nieskończoności, aby skalować go do rozmiaru kanwy:

Wynik wydaje się nieco mały, co sugeruje, że Bounds właściwość obiektu SKPath zgłasza rozmiar większy niż ścieżka.

Wewnętrznie Skia przybliża łuk przy użyciu wielu kwadratowych krzywych Béziera. Te krzywe (jak widać w następnej sekcji) zawierają punkty kontrolne, które określają sposób rysowania krzywej, ale nie są częścią renderowanej krzywej. Właściwość Bounds zawiera te punkty kontrolne.

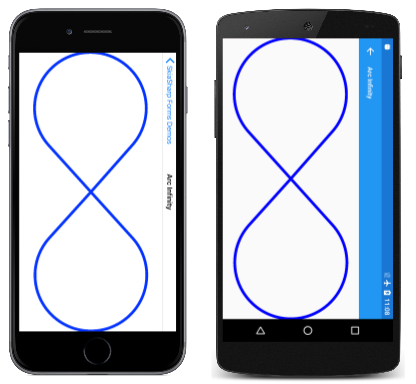
Aby uzyskać ściślejsze dopasowanie, użyj TightBounds właściwości , która wyklucza punkty sterowania. Oto program działający w trybie poziomym i używając TightBounds właściwości w celu uzyskania granic ścieżki:

Chociaż połączenia między łukami i liniami prostymi są matematycznie gładkie, zmiana z łuku na prostą może wydawać się nieco nagłe. Lepszy znak nieskończoności jest przedstawiony w następnym artykule na temat trzech typów krzywych Béziera.

Linki powiązane

• Interfejsy API skiaSharp