Udostępnij za pośrednictwem

System.Drawing.Drawing2D.Matrix, klasa

  • Artykuł

Ten artykuł zawiera dodatkowe uwagi dotyczące dokumentacji referencyjnej dla tego interfejsu API.

Klasa Matrix hermetyzuje macierz 3-by-3 affine reprezentującą transformację geometryczną.

W GDI+można przechowywać przekształcenie affine w Matrix obiekcie. Ponieważ trzecia kolumna macierzy reprezentująca przekształcenie affine jest zawsze (0, 0, 1), podczas konstruowania Matrix obiektu należy określić tylko sześć liczb w pierwszych dwóch kolumnach. Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) Instrukcja konstruuje macierz pokazaną na poniższym rysunku.

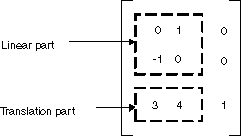
Macierzy.

Uwaga

W wersjach .NET 6 i nowszych pakiet System.Drawing.Common, który zawiera ten typ, jest obsługiwany tylko w systemach operacyjnych Windows. Użycie tego typu w aplikacjach międzyplatformowych powoduje ostrzeżenia w czasie kompilacji i wyjątki czasu wykonywania. Aby uzyskać więcej informacji, zobacz System.Drawing.Common supported only on Windows (Obsługiwane tylko w systemie Windows).

Przekształcenia złożone

Transformacja złożona to sekwencja przekształceń, po której następuje druga. Rozważ macierze i przekształcenia na poniższej liście:

Macierz Przekształcenie
Macierz A Obracanie 90 stopni
Macierz B Skalowanie według współczynnika 2 w kierunku x
Macierz C Przetłumacz 3 jednostki w kierunku y

Jeśli zaczniesz od punktu (2, 1) - reprezentowanego przez macierz [2 1 1] - i pomnożysz przez A, następnie B, A, a następnie C, punkt (2, 1) przejdzie trzy przekształcenia w podanej kolejności.

[2 1 1]ABC = [-2 5 1]

Zamiast przechowywać trzy części transformacji złożonej w trzech oddzielnych macierzach, można pomnożyć A, B i C razem, aby uzyskać pojedynczą macierz 3×3, która przechowuje całą transformację złożoną. Załóżmy, że ABC = D. Następnie punkt pomnożony przez D daje taki sam wynik jak punkt pomnożony przez A, a następnie B, a następnie C.

[2 1 1]D = [-2 5 1]

Poniższa ilustracja przedstawia macierze A, B, C i D.

Macierze A, B, C i D

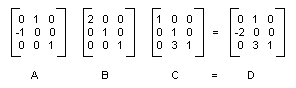
Fakt, że macierz przekształcenia złożonego można utworzyć przez pomnożenie poszczególnych macierzy transformacji oznacza, że każda sekwencja przekształceń affine może być przechowywana w jednym Matrix obiekcie.

Uwaga

Kolejność transformacji złożonej jest ważna. Ogólnie rzecz biorąc, obróć, a następnie skaluj, a następnie przetłumacz nie jest taka sama jak skala, a następnie obróć, a następnie przetłumacz. Podobnie kolejność mnożenia macierzy jest ważna. Ogólnie rzecz biorąc, ABC nie jest taki sam jak BAC.

Klasa Matrix udostępnia kilka metod tworzenia transformacji złożonej: Multiply, , Rotate, RotateAtScale, Shear, i Translate. Poniższy przykład tworzy macierz transformacji złożonej, która najpierw obraca 30 stopni, a następnie skaluje według współczynnika 2 w kierunku y, a następnie tłumaczy 5 jednostek w kierunku x:

Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);

Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)