Macierzowe przedstawienie transformacji
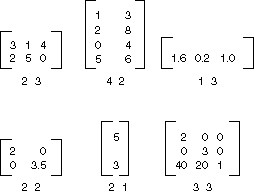
Macierz m×n to zestaw liczb rozmieszczonych w wierszach m i n kolumnach. Poniższa ilustracja przedstawia kilka macierzy.
Można dodać dwie macierze o tym samym rozmiarze, dodając poszczególne elementy. Na poniższej ilustracji przedstawiono dwa przykłady dodawania macierzy.
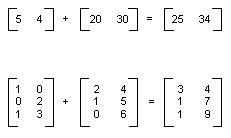
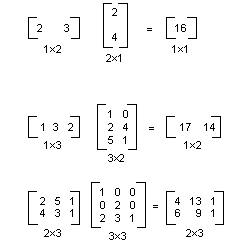
Macierz m×n może być mnożona przez macierz n×p, a wynik jest macierzą m×p. Liczba kolumn w pierwszej macierzy musi być taka sama jak liczba wierszy w drugiej macierzy. Na przykład macierz 4×2 można pomnożyć przez macierz 2×3 w celu utworzenia macierzy 4×3.
Punkty w płaszczyźnie i wierszach i kolumnach macierzy można traktować jako wektory. Na przykład (2, 5) jest wektorem z dwoma składnikami, a (3, 7, 1) jest wektorem z trzema składnikami. Kropka dwóch wektorów jest definiowana w następujący sposób:
(a, b) • (c, d) = ac + bd
(a, b, c) • (d, e, f) = ad + be + cf
Na przykład kropka (2, 3) i (5, 4) to (2)(5) + (3)(4) = 22. Kropka produktu (2, 5, 1) i (4, 3, 1) to (2)(4) + (5)(3) + (1)(1) = 24. Należy pamiętać, że kropka dwóch wektorów jest liczbą, a nie innym wektorem. Należy również pamiętać, że można obliczyć produkt kropkowy tylko wtedy, gdy dwa wektory mają taką samą liczbę składników.
Let A(i, j) być wpisem w macierzy A w wierszu i jth kolumny. Na przykład A(3, 2) jest wpisem w macierzy A w trzecim wierszu i drugiej kolumnie. Załóżmy, że macierze A, B i C są macierzami, a AB = C. Wpisy języka C są obliczane w następujący sposób:
C(i, j) = (wiersz i z A) • (kolumna j b)
Na poniższej ilustracji przedstawiono kilka przykładów mnożenia macierzy.
Jeśli myślisz o punkcie w płaszczyźnie jako macierzy 1×2, możesz przekształcić ten punkt, mnożąc go przez macierz 2×2. Na poniższej ilustracji przedstawiono kilka przekształceń zastosowanych do punktu (2, 1).
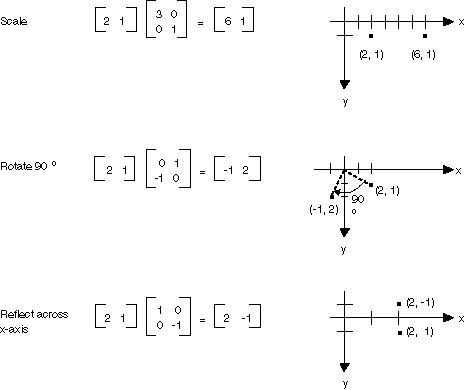
Wszystkie przekształcenia pokazane na powyższej ilustracji to przekształcenia liniowe. Niektóre inne przekształcenia, takie jak tłumaczenie, nie są liniowe i nie mogą być wyrażone jako mnożenie przez macierz 2×2. Załóżmy, że chcesz zacząć od punktu (2, 1), obróć go o 90 stopni, przetłumacz 3 jednostki w kierunku x i przetłumacz go na 4 jednostki w kierunku y. Można to zrobić przy użyciu mnożenia macierzy, po którym następuje dodanie macierzy.
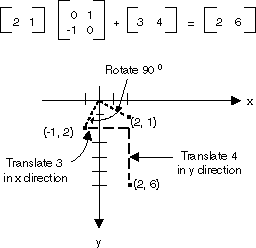
Transformacja liniowa (mnożenie przez macierz 2×2), po której następuje tłumaczenie (dodanie macierzy 1×2) jest nazywane przekształceniem affine. Alternatywą do przechowywania przekształcenia affine w parze macierzy (jednej dla części liniowej i jednej translacji) jest przechowywanie całej transformacji w macierzy 3×3. Aby wykonać tę pracę, punkt w płaszczyźnie musi być przechowywany w macierzy 1×3 z fikcyjną współrzędną 3. Zwykłą techniką jest uczynienie wszystkich współrzędnych 3 równych 1. Na przykład punkt (2, 1) jest reprezentowany przez macierz [2 1 1]. Na poniższej ilustracji przedstawiono przekształcenie affine (obróć 90 stopni; przetłumacz 3 jednostki w kierunku x, 4 jednostki w kierunku y) wyrażone jako mnożenie przez pojedynczą macierz 3×3.
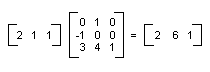
W poprzednim przykładzie punkt (2, 1) jest mapowany na punkt (2, 6). Należy pamiętać, że trzecia kolumna macierzy 3×3 zawiera liczby 0, 0, 1. Zawsze tak będzie w przypadku macierzy 3×3 przekształcenia affine. Ważne liczby to sześć liczb w kolumnach 1 i 2. Lewa górna część 2×2 macierzy reprezentuje liniową część przekształcenia, a pierwsze dwa wpisy w trzecim wierszu reprezentują tłumaczenie.
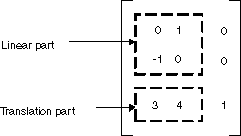
W GDI+ można przechowywać przekształcenie affine w Matrix obiekcie. Ponieważ trzecia kolumna macierzy reprezentująca przekształcenie affine jest zawsze (0, 0, 1), podczas konstruowania Matrix obiektu należy określić tylko sześć liczb w pierwszych dwóch kolumnach. Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) Instrukcja konstruuje macierz pokazaną na powyższym rysunku.
Przekształcenia złożone
Transformacja złożona to sekwencja przekształceń, po której następuje druga. Rozważ macierze i przekształcenia na poniższej liście:
| Matryca | Przekształcenie |
|---|---|
| Macierz A | Obracanie 90 stopni |
| Macierz B | Skalowanie według współczynnika 2 w kierunku x |
| Macierz C | Przetłumacz 3 jednostki w kierunku y |
Jeśli zaczniemy od punktu (2, 1) — reprezentowanego przez macierz [2 1 1] — i pomnożymy przez A, a następnie B, następnie C, punkt (2, 1) przejdzie trzy przekształcenia w podanej kolejności.
[2 1 1] ABC = [-2 5 1]
Zamiast przechowywać trzy części transformacji złożonej w trzech oddzielnych macierzach, można pomnożyć A, B i C razem, aby uzyskać pojedynczą macierz 3×3, która przechowuje całą transformację złożoną. Załóżmy, że ABC = D. Następnie punkt pomnożony przez D daje taki sam wynik jak punkt pomnożony przez A, a następnie B, a następnie C.
[2 1 1] D = [-2 5 1]
Poniższa ilustracja przedstawia macierze A, B, C i D.
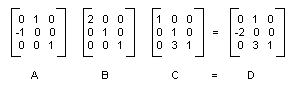
Fakt, że macierz przekształcenia złożonego można utworzyć przez pomnożenie poszczególnych macierzy transformacji oznacza, że każda sekwencja przekształceń affine może być przechowywana w jednym Matrix obiekcie.
Uwaga
Kolejność transformacji złożonej jest ważna. Ogólnie rzecz biorąc, obróć, a następnie skaluj, a następnie przetłumacz nie jest taka sama jak skala, a następnie obróć, a następnie przetłumacz. Podobnie kolejność mnożenia macierzy jest ważna. Ogólnie rzecz biorąc, ABC nie jest taki sam jak BAC.
Klasa Matrix udostępnia kilka metod tworzenia transformacji złożonej: Multiply, , Rotate, RotateAtScale, Shear, i Translate. Poniższy przykład tworzy macierz transformacji złożonej, która najpierw obraca 30 stopni, a następnie skaluje według współczynnika 2 w kierunku y, a następnie tłumaczy 5 jednostek w kierunku x:
Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);
Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)
Poniższa ilustracja przedstawia macierz.

Zobacz też
.NET Desktop feedback
