Udostępnij za pośrednictwem

Krzywe kardynalne w GDI+

  • Artykuł

Linia kardynalna to sekwencja pojedynczych krzywych sprzężonych w celu utworzenia większej krzywej. Linia spline jest określana przez tablicę punktów i parametr napięcia. Linia kardynaalna przechodzi płynnie przez każdy punkt w tablicy; nie ma ostrych narożników i nie ma nagłych zmian w ciasności krzywej. Poniższa ilustracja przedstawia zestaw punktów i kardynaną krzywą, która przechodzi przez każdy punkt w zestawie.

Cardinal Spline

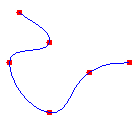
Linie fizyczne i matematyczne

Fizyczna krzywa to cienki kawałek drewna lub innego elastycznego materiału. Przed pojawieniem się matematycznych linii krzywych projektanci używali fizycznych linii do rysowania krzywych. Projektant umieści krzywą na kawałku papieru i zakotwiczy go do danego zestawu punktów. Projektant może następnie utworzyć krzywą, rysując wzdłuż linii spline piórem lub ołówkiem. Dany zestaw punktów może przynieść różne krzywe, w zależności od właściwości fizycznej linii spline. Na przykład linia spline o wysokiej odporności na zginanie powoduje powstanie innej krzywej niż niezwykle elastyczna linia spline.

Formuły matematycznych linii krzywych są oparte na właściwościach elastycznych prętów, więc krzywe generowane przez matematyczne linie są podobne do krzywych, które były kiedyś produkowane przez fizyczne linie. Podobnie jak fizyczne linie różnych napięć spowodują różne krzywe przez dany zestaw punktów, matematyczne linie z różnymi wartościami parametru napięcia będą produkować różne krzywe przez dany zestaw punktów. Na poniższej ilustracji przedstawiono cztery linie kardynaalne przechodzące przez ten sam zestaw punktów. Napięcie jest wyświetlane dla każdej linii spline. Napięcie 0 odpowiada nieskończonym napięciu fizycznemu, zmuszając krzywą do podjęcia najkrótszej drogi (linii prostych) między punktami. Napięcie 1 nie odpowiada napięciu fizycznemu, dzięki czemu spline może podjąć ścieżkę najmniej całkowitego zginania. Z wartościami napięcia większymi niż 1 krzywa zachowuje się jak ściśnięta sprężyna, popchnięta do dłuższej ścieżki.

Cardinal Splines

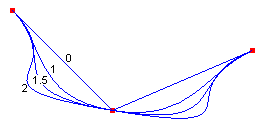
Cztery szprychy na poprzedniej ilustracji mają tę samą linię tangensową w punkcie początkowym. Tangens jest linią wyciągniętą od punktu początkowego do następnego punktu wzdłuż krzywej. Podobnie współdzielona tangens w punkcie końcowym jest linią wyciągniętą z punktu końcowego do poprzedniego punktu na krzywej.

Aby narysować kardynaną krzywą, potrzebne jest wystąpienie Graphics klasy , Peni tablica Point obiektów Wystąpienie Graphics klasy udostępnia DrawCurve metodę, która rysuje linię spline, a Pen atrybuty linii spline, takie jak szerokość linii linii i kolor linii. Tablica Point obiektów przechowuje punkty, przez które będzie przechodzić krzywa. W poniższym przykładzie kodu pokazano, jak narysować kardynaną linię spline przechodzącą przez punkty w pliku myPointArray. Trzeci parametr to napięcie.

myGraphics.DrawCurve(myPen, myPointArray, 1.5f);

myGraphics.DrawCurve(myPen, myPointArray, 1.5F)

Zobacz też