Samouczek: implementowanie kwantowego generatora liczb losowych w programie Q#

W tym samouczku nauczysz się pisać podstawowy program kwantowy, który Q# wykorzystuje charakter mechaniki kwantowej do tworzenia liczby losowej.

Ten samouczek obejmuje następujące kroki:

• Utwórz Q# program.
• Przejrzyj główne składniki Q# programu.
• Zdefiniuj logikę problemu.
• Łączenie operacji klasycznych i kwantowych w celu rozwiązania problemu.
• Praca z kubitami i superpozycją w celu utworzenia kwantowego generatora liczb losowych.

Napiwek

Jeśli chcesz przyspieszyć podróż obliczeń kwantowych, zapoznaj się z kodem w usłudze Azure Quantum, unikatową funkcją witryny internetowej Azure Quantum. W tym miejscu możesz uruchamiać wbudowane Q# przykłady lub własne Q# programy, generować nowy Q# kod z monitów, otwierać i uruchamiać kod w programie VS Code dla sieci Web jednym kliknięciem i zadawać Copilot wszelkie pytania dotyczące obliczeń kwantowych.

Wymagania wstępne

• Aby uruchomić przykładowy kod w aplikacji Copilot w usłudze Azure Quantum:

  • Konto e-mail microsoft (MSA).

• Aby utworzyć i uruchomić przykładowy kod w programie Visual Studio Code:

  • Najnowsza wersja programu Visual Studio Code lub otwórz program VS Code w sieci Web.

  • Najnowsza wersja rozszerzeniaQuantum Development KitAzure. Aby uzyskać szczegółowe informacje na temat instalacji, zobacz Konfigurowanie rozszerzenia zestawu QDK.

  • Jeśli chcesz używać notesów Jupyter Notebook, musisz również zainstalować rozszerzenia Python i Jupyter oraz najnowszy qsharp pakiet języka Python. Aby to zrobić, otwórz terminal i uruchom następujące polecenie:

    $ pip install --upgrade  qsharp
    

Definiowanie problemu

Komputery klasyczne nie generują liczb losowych, ale raczej pseudorandom . Generator liczb pseudorandom generuje deterministyczną sekwencję liczb na podstawie określonej wartości początkowej, nazywanej inicjatorem. Aby lepiej przybliżyć wartości losowe, ten inicjator często jest bieżącą godziną z zegara procesora CPU.

Z drugiej strony komputery kwantowe mogą generować prawdziwie losowe liczby. Wynika to z faktu, że pomiar kubitu w superpozycji jest procesem probabilistycznym. Wynik pomiaru jest losowy i nie ma możliwości przewidywania wyniku. Jest to podstawowa zasada kwantowych generatorów liczb losowych.

Kubit to jednostka informacji kwantowych, które mogą znajdować się w superpozycji. W przypadku pomiaru kubit może znajdować się tylko w stanie 0 lub w stanie 1 . Jednak przed pomiarem stan kubitu reprezentuje prawdopodobieństwo odczytu wartości 0 lub 1 z pomiarem.

Zacznij od utworzenia kubitu w stanie podstawy, na przykład zero. Pierwszym krokiem generatora liczb losowych jest użycie operacji Hadamard , aby umieścić kubit w równej superpozycji. Pomiar tego stanu powoduje zero lub jeden z 50% prawdopodobieństwem każdego wyniku, co jest naprawdę losowym bitem.

Nie ma możliwości poznania tego, co otrzymasz po pomiarze kubitu w superpozycji, a wynik jest inną wartością przy każdym wywołaniu kodu. Ale jak można użyć tego zachowania, aby wygenerować większe liczby losowe?

Załóżmy, że powtarzasz ten proces cztery razy, generując następującą sekwencję cyfr binarnych:

$${0, 1, 1, 0}$$

Jeśli połączysz te bity w ciąg bitów, możesz utworzyć większą liczbę. W tym przykładzie sekwencja bitowa ${0110}$ jest równa liczbie sześć w postaci dziesiętnej.

$${0110_{\ binary} \equiv 6_{\ decimal}}$$

W przypadku wielokrotnego powtarzania tego procesu można połączyć wiele bitów, aby utworzyć dowolną dużą liczbę. Korzystając z tej metody, można utworzyć liczbę do użycia jako bezpieczne hasło, ponieważ możesz mieć pewność, że żaden haker nie może określić wyników sekwencji pomiarów.

Definiowanie logiki generatora liczb losowych

Określmy, jaka powinna być logika generatora liczb losowych:

1. Zdefiniuj max jako maksymalną liczbę, którą chcesz wygenerować.
2. Zdefiniuj liczbę bitów losowych, które należy wygenerować. Można to zrobić, obliczając liczbę bitów, nBits, należy wyrazić liczby całkowite do max.
3. Wygeneruj losowy ciąg bitowy o długości nBits.
4. Jeśli ciąg bitowy reprezentuje liczbę większą niż max, wróć do kroku trzeciego.
5. W przeciwnym razie proces zostanie zakończony. Zwróć wygenerowaną liczbę jako liczbę całkowitą.

Załóżmy na przykład, że wartość max wynosi 12. Oznacza to, że 12 jest największą liczbą, której chcesz użyć jako hasła.

Potrzebujesz ${\lfloor ln(12) / ln(2) + 1 \rfloor}$, lub 4 bity do reprezentowania liczby z zakresu od 0 do 12. Możemy użyć wbudowanej funkcji BitSizeI, która przyjmuje dowolną liczbę całkowitą i zwraca liczbę bitów wymaganych do jej reprezentowania.

Załóżmy, że wygenerujesz ciąg bitowy ${1101_{\ binary}}$, który jest odpowiednikiem ciągu ${13_{\ decimal}}$. Ponieważ 13 jest większe niż 12, należy powtórzyć proces.

Następnie wygenerujesz ciąg bitowy ${0110_{\ binary}}$, który jest odpowiednikiem ciągu ${6_{\ decimal}}$. Ponieważ 6 jest mniejsze niż 12, proces jest zakończony.

Kwantowy generator liczb losowych zwróci numer 6 jako hasło. W praktyce ustaw większą liczbę jako maksymalną, ponieważ mniejsze liczby są łatwe do złamania, po prostu próbując wszystkie możliwe hasła. W rzeczywistości, aby zwiększyć trudności z odgadnięciem lub pęknięciem hasła, można użyć kodu ASCII, aby przekonwertować plik binarny na tekst i wygenerować hasło przy użyciu cyfr, symboli i liter mieszanych.

Pisanie generatora bitów losowych

Pierwszym krokiem jest napisanie Q# operacji, która generuje losowy bit. Ta operacja będzie jednym z bloków konstrukcyjnych generatora liczb losowych.

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

Teraz przyjrzyj się nowej kodzie.

• Definiujesz operację GenerateRandomBit , która nie przyjmuje żadnych danych wejściowych i generuje wartość typu Result. Typ Result reprezentuje wynik pomiaru i może mieć dwie możliwe wartości: Zero lub One.
• Przydzielisz jeden kubit za pomocą słowa kluczowego use . Po przydzieleniu kubit jest zawsze w stanie |0.
• Operacja służy H do umieszczania kubitu w równej superpozycji.
• Operacja służy M do mierzenia kubitu, zwracania zmierzonej wartości (Zero lub One).
• Operacja służy do resetowania Reset kubitu do stanu |0}.

Umieszczając kubit w superpozycji z H operacją i mierząc go za M pomocą operacji, wynik jest inną wartością za każdym razem, gdy kod jest wywoływany.

Wizualizowanie kodu za Q# pomocą sfery Bloch

Na sferze Blocha biegun północny reprezentuje wartość klasyczną 0, a biegun południowy reprezentuje wartość klasyczną 1. Każdą superpozycję można przedstawić jako punkt na sferze (reprezentowany przez strzałkę). Im bliżej od końca strzałki do bieguna, tym większe jest prawdopodobieństwo, że przy pomiarze kubit ulegnie kolapsowi do wartości klasycznej przypisanej do tego bieguna. Na przykład stan kubitu reprezentowany przez strzałkę na poniższej ilustracji ma większe prawdopodobieństwo podania wartości 0 , jeśli ją zmierzysz.

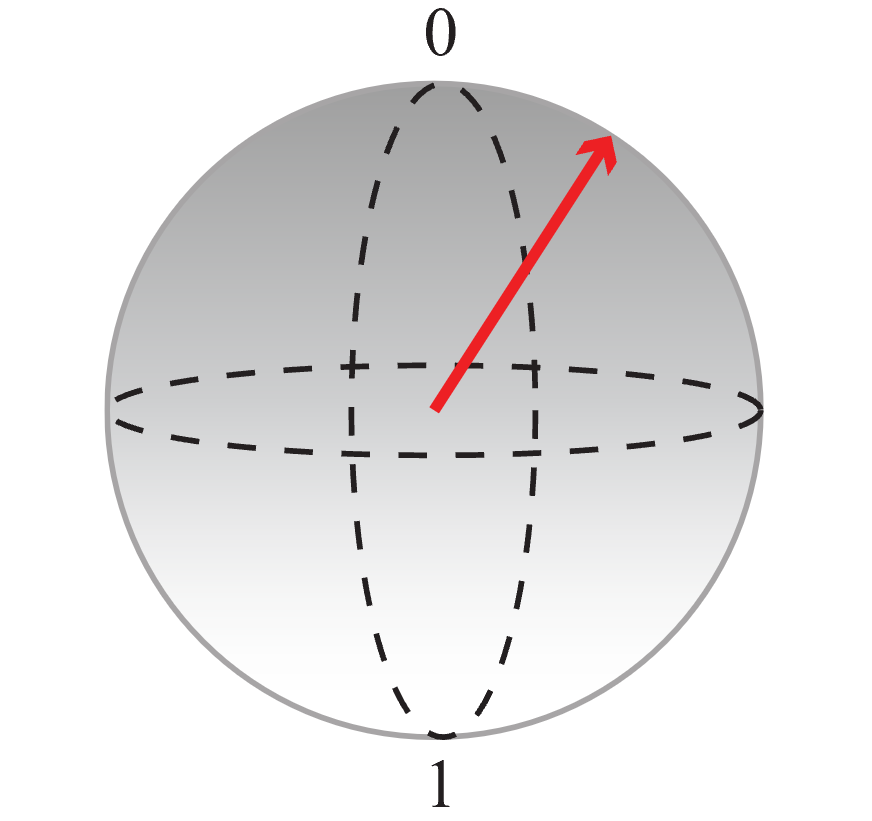
Ta reprezentacja umożliwia wizualizowanie działania kodu:

1. Najpierw zacznij od kubitu zainicjowanego w stanie |0} i zastosuj operację H , aby utworzyć równą superpozycję, w której prawdopodobieństwa dla wartości 0 i 1 są takie same.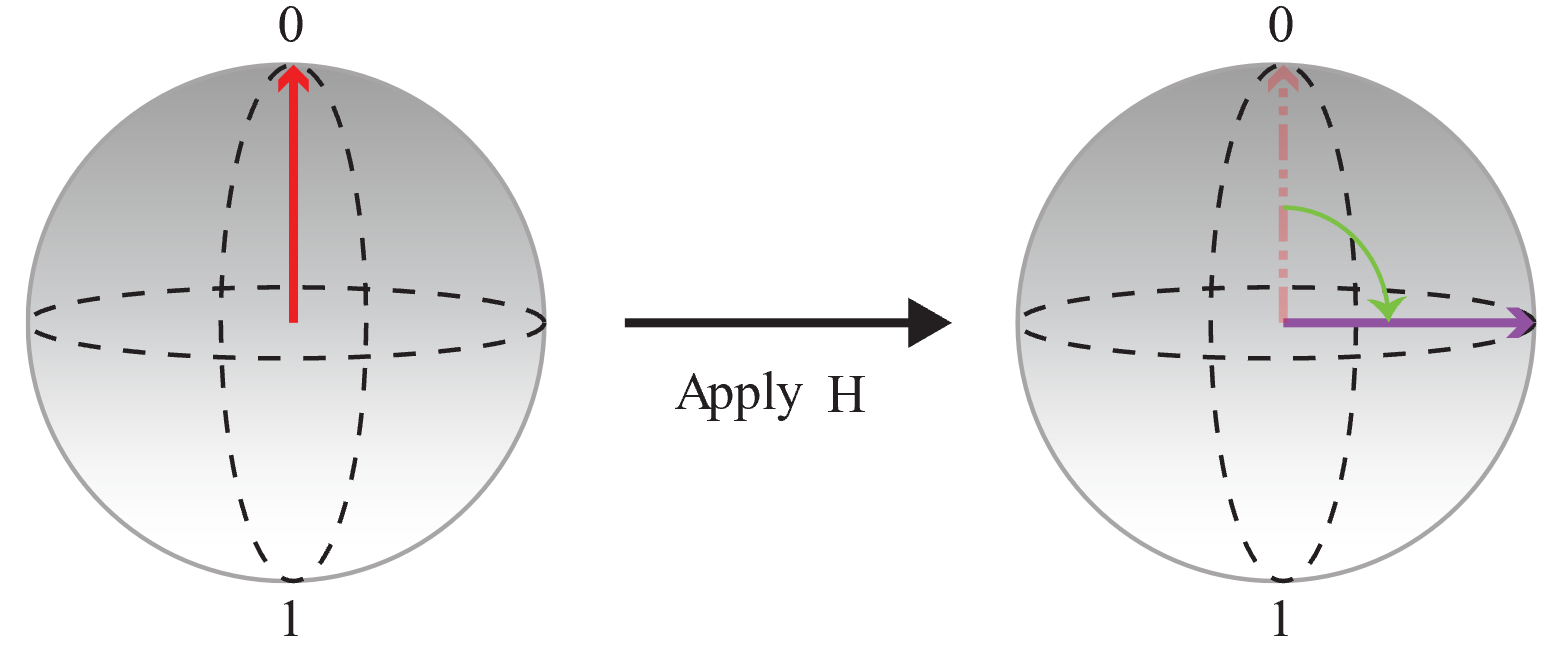

   

2. Następnie zmierz kubit i zapisz dane wyjściowe:

   

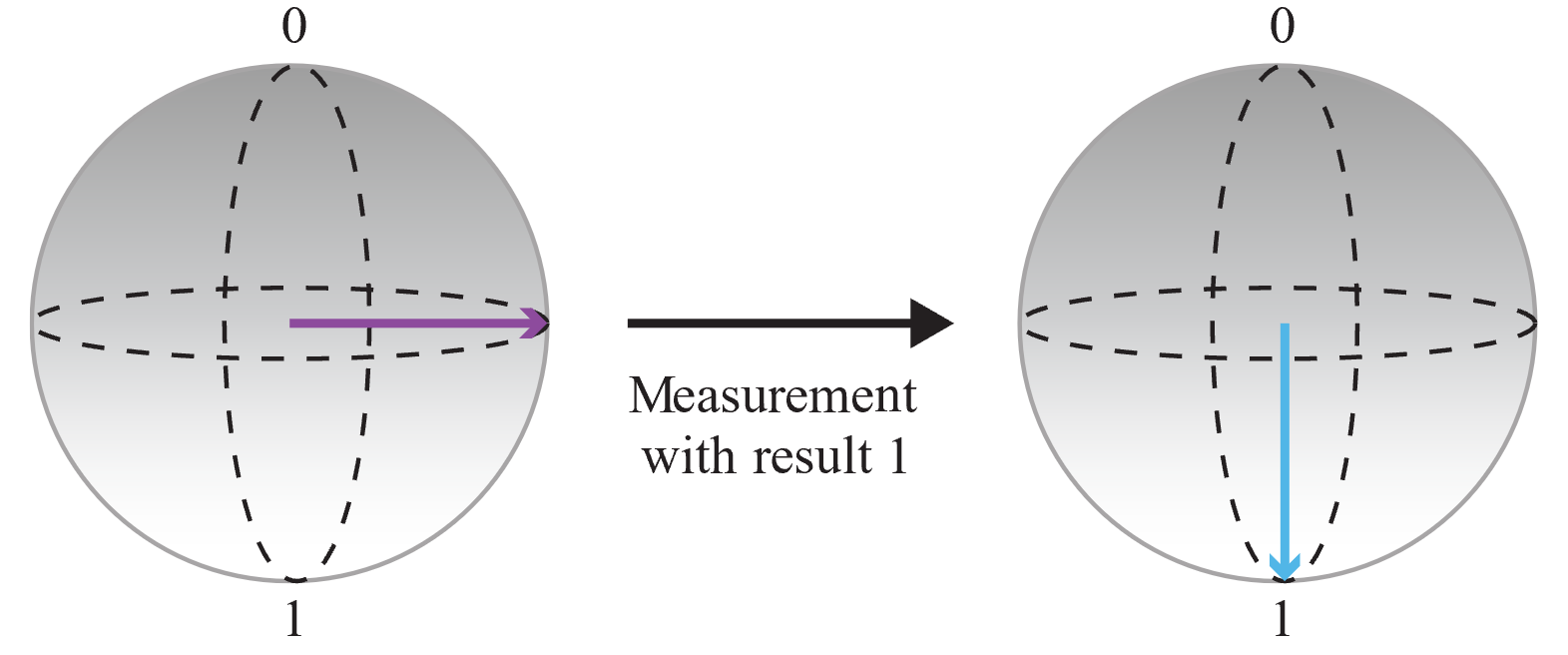
Ponieważ wynik pomiaru jest losowy, a prawdopodobieństwa pomiaru 0 i 1 są takie same, uzyskaliśmy całkowicie losowy bit. Tę operację można wywołać kilka razy, aby utworzyć liczby całkowite. Jeśli na przykład wywołasz operację trzy razy, aby uzyskać trzy losowe bity, możesz utworzyć losowe liczby 3-bitowe (czyli losową liczbę z zakresu od 0 do 7).

Pisanie kompletnego generatora liczb losowych

1. Najpierw należy zaimportować wymagane przestrzenie nazw z biblioteki standardowej Q# do programu. Q# Kompilator ładuje wiele typowych funkcji i operacji automatycznie, jednak w przypadku kompletnego generatora liczb losowych potrzebne są pewne dodatkowe funkcje i operacje z dwóch Q# przestrzeni nazw: Microsoft.Quantum.Mathi Microsoft.Quantum.Convert.

   import Microsoft.Quantum.Convert.*;
   import Microsoft.Quantum.Math.*;
   

2. Następnie zdefiniujesz operację GenerateRandomNumberInRange . Ta operacja wielokrotnie wywołuje operację GenerateRandomBit, aby utworzyć ciąg bitów.

   /// Generates a random number between 0 and `max`.
   operation GenerateRandomNumberInRange(max : Int) : Int {
       // Determine the number of bits needed to represent `max` and store it
       // in the `nBits` variable. Then generate `nBits` random bits which will
       // represent the generated random number.
       mutable bits = [];
       let nBits = BitSizeI(max);
       for idxBit in 1..nBits {
           bits += [GenerateRandomBit()];
       }
       let sample = ResultArrayAsInt(bits);
   
       // Return random number if it is within the requested range.
       // Generate it again if it is outside the range.
       return sample > max ? GenerateRandomNumberInRange(max) | sample;
   }
   
   

   Poświęćmy chwilę na przejrzenie nowego kodu.

   • Musisz obliczyć liczbę bitów potrzebnych do wyrażenia liczb całkowitych do max. Funkcja BitSizeI z Microsoft.Quantum.Math przestrzeni nazw konwertuje liczbę całkowitą na liczbę bitów potrzebnych do jej reprezentowania.
   • Operacja SampleRandomNumberInRange używa pętli for do generowania liczb losowych do momentu wygenerowania takiej liczby, która jest równa lub mniejsza niż max. Pętla for działa dokładnie tak samo jak pętla for w innych językach programowania.
   • Zmienna bits jest zmienną modyfikowalnym. Zmienna modyfikowalna to taka, która może się zmienić podczas obliczania. Aby zmienić wartość zmiennej modyfikowalnej, należy użyć dyrektywy set.
   • Funkcja ResultArrayAsInt z domyślnej Microsoft.Quantum.Convert przestrzeni nazw konwertuje ciąg bitowy na dodatnią liczbę całkowitą.

3. Na koniec dodasz punkt wejścia do programu. Domyślnie Q# kompilator wyszukuje operację Main i rozpoczyna przetwarzanie. Wywołuje operację GenerateRandomNumberInRange , aby wygenerować losową liczbę z zakresu od 0 do 100.

   operation Main() : Int {
       let max = 100;
       Message($"Sampling a random number between 0 and {max}: ");
   
       // Generate random number in the 0..max range.
       return GenerateRandomNumberInRange(max);
   }
   

   Dyrektywa let deklaruje zmienne, które nie zmieniają się podczas obliczania. W tym miejscu zdefiniujesz wartość maksymalną jako 100.

   Aby uzyskać więcej informacji na temat Main operacji, zobacz Punkty wejścia.

4. Kompletny kod generatora liczb losowych jest następujący:

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using a Hadamard operation
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

Uruchamianie programu generatora liczb losowych

Program można uruchomić w copilot w usłudze Azure Quantum i w programie Visual Studio Code jako aplikacji autonomicznej Q# lub przy użyciu programu hosta języka Python.

Copilot w usłudze Azure Quantum

Kod możesz przetestować Q# za pomocą rozwiązania Copilot w usłudze Azure Quantum bezpłatnie — wystarczy konto e-mail microsoft (MSA). Aby uzyskać więcej informacji na temat rozwiązania Copilot w usłudze Azure Quantum, zobacz Eksplorowanie usługi Azure Quantum.

1. Otwórz aplikację Copilot w usłudze Azure Quantum w przeglądarce.

2. Skopiuj i wklej następujący kod do edytora kodu.

   import Microsoft.Quantum.Convert.*;
   import Microsoft.Quantum.Math.*;
   
   operation Main() : Int {
       let max = 100;
       Message($"Sampling a random number between 0 and {max}: ");
   
       // Generate random number in the 0..max range.
       return GenerateRandomNumberInRange(max);
   }
   
   /// # Summary
   /// Generates a random number between 0 and `max`.
   operation GenerateRandomNumberInRange(max : Int) : Int {
       // Determine the number of bits needed to represent `max` and store it
       // in the `nBits` variable. Then generate `nBits` random bits which will
       // represent the generated random number.
       mutable bits = [];
       let nBits = BitSizeI(max);
       for idxBit in 1..nBits {
           bits += [GenerateRandomBit()];
       }
       let sample = ResultArrayAsInt(bits);
   
       // Return random number if it is within the requested range.
       // Generate it again if it is outside the range.
       return sample > max ? GenerateRandomNumberInRange(max) | sample;
   }
   
   /// # Summary
   /// Generates a random bit.
   operation GenerateRandomBit() : Result {
       // Allocate a qubit.
       use q = Qubit();
   
       // Set the qubit into superposition of 0 and 1 using the Hadamard 
       // operation `H`.
       H(q);
   
       // At this point the qubit `q` has 50% chance of being measured in the
       // |0〉 state and 50% chance of being measured in the |1〉 state.
       // Measure the qubit value using the `M` operation, and store the
       // measurement value in the `result` variable.
       let result = M(q);
   
       // Reset qubit to the |0〉 state.
       // Qubits must be in the |0〉 state by the time they are released.
       Reset(q);
   
       // Return the result of the measurement.
       return result;
   
       // Note that Qubit `q` is automatically released at the end of the block.
   }
   
   

3. Wybierz liczbę zdjęć do uruchomienia, a następnie wybierz pozycję Uruchom.

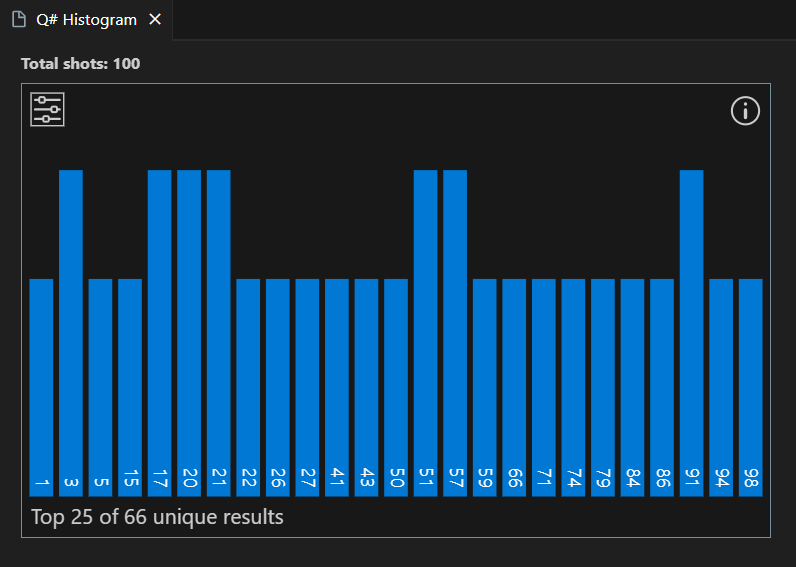
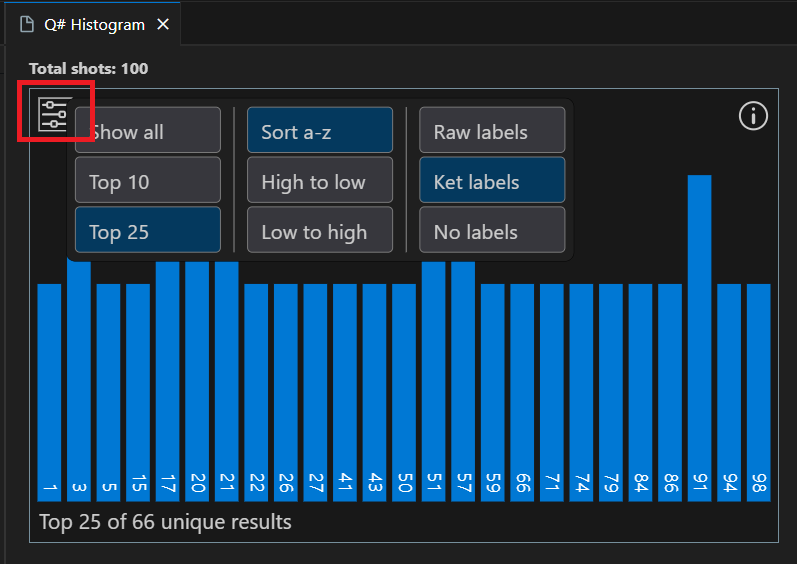
4. Wyniki są wyświetlane w histogramie i w polach Wyniki .

5. Wybierz pozycję Wyjaśnij kod , aby wyświetlić monit Copilot o wyjaśnienie kodu.

Napiwek

W aplikacji Copilot w usłudze Azure Quantum możesz otworzyć program w programie VS Code dla sieci Web , wybierając przycisk logo programu VS Code w prawym rogu edytora kodu.

Q# program w programie Visual Studio Code

1. Otwórz program Visual Studio Code i wybierz pozycję Plik > nowy plik tekstowy, aby utworzyć nowy plik.

2. Zapisz plik jako RandomNumberGenerator.qs. Ten plik będzie zawierać Q# kod programu.

3. Skopiuj następujący kod w RandomNumberGenerator.qs pliku.

   
   import Microsoft.Quantum.Convert.*;
   import Microsoft.Quantum.Math.*;
   
   operation Main() : Int {
       let max = 100;
       Message($"Sampling a random number between 0 and {max}: ");
   
       // Generate random number in the 0..max range.
       return GenerateRandomNumberInRange(max);
   }
   
   /// # Summary
   /// Generates a random number between 0 and `max`.
   operation GenerateRandomNumberInRange(max : Int) : Int {
       // Determine the number of bits needed to represent `max` and store it
       // in the `nBits` variable. Then generate `nBits` random bits which will
       // represent the generated random number.
       mutable bits = [];
       let nBits = BitSizeI(max);
       for idxBit in 1..nBits {
           bits += [GenerateRandomBit()];
       }
       let sample = ResultArrayAsInt(bits);
   
       // Return random number if it is within the requested range.
       // Generate it again if it is outside the range.
       return sample > max ? GenerateRandomNumberInRange(max) | sample;
   }
   
   /// # Summary
   /// Generates a random bit.
   operation GenerateRandomBit() : Result {
       // Allocate a qubit.
       use q = Qubit();
   
       // Set the qubit into superposition of 0 and 1 using the Hadamard 
       // operation `H`.
       H(q);
   
       // At this point the qubit `q` has 50% chance of being measured in the
       // |0〉 state and 50% chance of being measured in the |1〉 state.
       // Measure the qubit value using the `M` operation, and store the
       // measurement value in the `result` variable.
       let result = M(q);
   
       // Reset qubit to the |0〉 state.
       // Qubits must be in the |0〉 state by the time they are released.
       Reset(q);
   
       // Return the result of the measurement.
       return result;
   
       // Note that Qubit `q` is automatically released at the end of the block.
   }
   
   

4. Przed uruchomieniem programu należy ustawić target profil na Bez ograniczeń. Wybierz pozycję Widok — paleta poleceń, wyszukaj pozycję QIR, wybierz pozycję >: Ustaw profil QIR Q# usługi Azure Quantum, a następnie wybierz pozycjętarget : bez ograniczeń.Q#

5. Aby uruchomić program, wybierz pozycję Uruchom Q# plik z listy rozwijanej ikona odtwarzania w prawym górnym rogu, wybierz pozycję Uruchom z listy poleceń poprzedzających Main()polecenie lub naciśnij Ctrl+F5. Program uruchamia operację Main() w domyślnym symulatorze.

   

6. Dane wyjściowe zostaną wyświetlone w konsoli debugowania.

7. Uruchom ponownie program, aby zobaczyć inny wynik.

Uwaga

target Jeśli profil nie jest ustawiony na Unrestricted, podczas uruchamiania programu zostanie wyświetlony błąd.

Wykreślenie histogramu częstotliwości

Zwizualizujmy rozkład wyników uzyskanych z wielokrotnego uruchamiania programu kwantowego. Histogram częstotliwości pomaga wizualizować rozkład prawdopodobieństwa tych wyników.

1. Wybierz pozycję Widok —> paleta poleceń i wpisz "histogram", który wyświetla Q#. Możesz również wybrać pozycję Histogram z listy poleceń poprzedzających Main()polecenie . Wybierz tę opcję, aby otworzyć okno histogramu Q# .

   

2. Wprowadź liczbę zdjęć do wykonania programu, na przykład 100 zdjęć, a następnie naciśnij Enter. Histogram zostanie wyświetlony w oknie histogramu Q# .

3. Każdy słupek w histogramie odpowiada możliwemu wynikowi, a jego wysokość reprezentuje liczbę obserwowanych wyników. Liczba różnych wyników może się różnić za każdym razem, gdy uruchamiasz histogram.

   

   Napiwek

   Histogram można powiększyć za pomocą kółka przewijania myszy lub gestu klawiatury. Po powiększeniu można przesuwać wykres, naciskając "Alt" podczas przewijania.

4. Wybierz pasek, aby wyświetlić procent tego wyniku.

5. Wybierz ikonę ustawień w lewym górnym rogu, aby wyświetlić opcje. Możesz wyświetlić 10 pierwszych wyników, 25 pierwszych wyników lub wszystkie wyniki. Możesz również posortować wyniki z wysokiej do niskiej lub niskiej do wysokiej.

   

Notes Jupyter w programie VS Code

1. W programie VS Code wybierz pozycję > poleceń i wybierz pozycję Utwórz: nowy notes Jupyter.

2. W pierwszej komórce zaimportuj qsharp pakiet w kodzie języka Python:

   import qsharp
   

3. Q# Dodaj kod dla kwantowego programu generatora liczb losowych. W tym celu użyj %%qsharp polecenia magic. Zwróć uwagę, że %%qsharp polecenie zmienia komórkę notesu z typu Python na typ Q#. Skopiuj ten kod do drugiej komórki.

   %%qsharp
   
   import Microsoft.Quantum.Convert.*;
   import Microsoft.Quantum.Math.*;
   
   operation Main() : Int {
       let max = 100;
   
       // Generate random number in the 0..max range.
       return GenerateRandomNumberInRange(max);
   }
   
   /// # Summary
   /// Generates a random number between 0 and `max`.
   operation GenerateRandomNumberInRange(max : Int) : Int {
       // Determine the number of bits needed to represent `max` and store it
       // in the `nBits` variable. Then generate `nBits` random bits which will
       // represent the generated random number.
       mutable bits = [];
       let nBits = BitSizeI(max);
       for idxBit in 1..nBits {
           bits += [GenerateRandomBit()];
       }
       let sample = ResultArrayAsInt(bits);
   
       // Return random number if it is within the requested range.
       // Generate it again if it is outside the range.
       return sample > max ? GenerateRandomNumberInRange(max) | sample;
   }
   
   /// # Summary
   /// Generates a random bit.
   operation GenerateRandomBit() : Result {
       // Allocate a qubit.
       use q = Qubit();
   
       // Set the qubit into superposition of 0 and 1 using the Hadamard 
       // operation `H`.
       H(q);
   
       // At this point the qubit `q` has 50% chance of being measured in the
       // |0〉 state and 50% chance of being measured in the |1〉 state.
       // Measure the qubit value using the `M` operation, and store the
       // measurement value in the `result` variable.
       let result = M(q);
   
       // Reset qubit to the |0〉 state.
       // Qubits must be in the |0〉 state by the time they are released.
       Reset(q);
   
       // Return the result of the measurement.
       return result;
   
       // Note that Qubit `q` is automatically released at the end of the block.
   }
   

4. Na koniec uruchom kod. Tę samą symulację można uruchomić niezależnie. Każda niezależna symulacja jest nazywana "strzałem". Na przykład uruchomimy symulację 100 razy.

   results = qsharp.run("Main()", shots=100)
   print(results)
   

Uwaga

Ten fragment kodu nie jest obecnie uruchamiany na żadnym dostępnym sprzęcie targetsAzure Quantum, ponieważ obiekt wywołujący ResultArrayAsInt wymaga QPU z pełnym profilem obliczeniowym.

Powiązana zawartość

Zapoznaj się z innymi Q# samouczkami:

• Splątanie kwantowe pokazuje, jak napisać Q# program, który manipuluje kubitami i mierzy je oraz demonstruje skutki superpozycji i splątania.
• Algorytm wyszukiwania Grovera pokazuje, jak napisać Q# program korzystający z algorytmu wyszukiwania Grovera.
• Quantum Fourier Transforms bada sposób pisania Q# programu, który bezpośrednio dotyczy określonych kubitów.
• Quantum Katas to samouczki samodzielne i ćwiczenia programistyczne mające na celu nauczanie elementów obliczeń kwantowych i Q# programowania w tym samym czasie.