Różne sposoby uruchamiania narzędzia do szacowania zasobów
Z tego artykułu dowiesz się, jak pracować z narzędziem do szacowania zasobów usługi Azure Quantum. Narzędzie do szacowania zasobów pomaga oszacować zasoby wymagane do uruchomienia programu kwantowego na komputerze kwantowym. Narzędzie do szacowania zasobów umożliwia oszacowanie liczby kubitów, liczby bram i głębokości obwodu wymaganego do uruchomienia programu kwantowego.
Narzędzie do szacowania zasobów jest dostępne w programie Visual Studio Code z rozszerzeniem Quantum Development Kit. Aby uzyskać więcej informacji, zobacz Zainstaluj Quantum Development Kit.
Ostrzeżenie
Narzędzie do szacowania zasobów w witrynie Azure Portal jest przestarzałe. Zalecamy przejście do lokalnego narzędzia do szacowania zasobów w programie Visual Studio Code podanym w Quantum Development Kit.
Wymagania wstępne dotyczące programu VS Code
- Najnowsza wersja programu Visual Studio Code lub otwórz program VS Code w sieci Web.
- Najnowsza wersja rozszerzenia Quantum Development Kit. Aby uzyskać szczegółowe informacje na temat instalacji, zobacz Konfigurowanie rozszerzenia zestawu QDK.
Napiwek
Nie musisz mieć konta platformy Azure, aby uruchomić narzędzie do szacowania zasobów.
Tworzenie nowego pliku języka Q#
- Otwórz program Visual Studio Code i wybierz pozycję Plik > nowy plik tekstowy, aby utworzyć nowy plik.
- Zapisz plik jako
ShorRE.qs. Ten plik będzie zawierać kod języka Q# dla programu.
Tworzenie algorytmu kwantowego
Skopiuj następujący kod do ShorRE.qs pliku:
import Std.Arrays.*;
import Std.Canon.*;
import Std.Convert.*;
import Std.Diagnostics.*;
import Std.Math.*;
import Std.Measurement.*;
import Microsoft.Quantum.Unstable.Arithmetic.*;
import Std.ResourceEstimation.*;
operation Main() : Unit {
let bitsize = 31;
// When choosing parameters for `EstimateFrequency`, make sure that
// generator and modules are not co-prime
let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize);
}
// In this sample we concentrate on costing the `EstimateFrequency`
// operation, which is the core quantum operation in Shors algorithm, and
// we omit the classical pre- and post-processing.
/// # Summary
/// Estimates the frequency of a generator
/// in the residue ring Z mod `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order (period)
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## bitsize
/// Number of bits needed to represent the modulus.
///
/// # Output
/// The numerator k of dyadic fraction k/2^bitsPrecision
/// approximating s/r.
operation EstimateFrequency(
generator : Int,
modulus : Int,
bitsize : Int
)
: Int {
mutable frequencyEstimate = 0;
let bitsPrecision = 2 * bitsize + 1;
// Allocate qubits for the superposition of eigenstates of
// the oracle that is used in period finding.
use eigenstateRegister = Qubit[bitsize];
// Initialize eigenstateRegister to 1, which is a superposition of
// the eigenstates we are estimating the phases of.
// We first interpret the register as encoding an unsigned integer
// in little endian encoding.
ApplyXorInPlace(1, eigenstateRegister);
let oracle = ApplyOrderFindingOracle(generator, modulus, _, _);
// Use phase estimation with a semiclassical Fourier transform to
// estimate the frequency.
use c = Qubit();
for idx in bitsPrecision - 1..-1..0 {
within {
H(c);
} apply {
// `BeginEstimateCaching` and `EndEstimateCaching` are the operations
// exposed by Azure Quantum Resource Estimator. These will instruct
// resource counting such that the if-block will be executed
// only once, its resources will be cached, and appended in
// every other iteration.
if BeginEstimateCaching("ControlledOracle", SingleVariant()) {
Controlled oracle([c], (1 <<< idx, eigenstateRegister));
EndEstimateCaching();
}
R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c);
}
if MResetZ(c) == One {
frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx);
}
}
// Return all the qubits used for oracles eigenstate back to 0 state
// using Microsoft.Quantum.Intrinsic.ResetAll.
ResetAll(eigenstateRegister);
return frequencyEstimate;
}
/// # Summary
/// Interprets `target` as encoding unsigned little-endian integer k
/// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where
/// p is `power`, g is `generator` and N is `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order ( period )
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## power
/// Power of `generator` by which `target` is multiplied.
/// ## target
/// Register interpreted as little endian encoded which is multiplied by
/// given power of the generator. The multiplication is performed modulo
/// `modulus`.
internal operation ApplyOrderFindingOracle(
generator : Int, modulus : Int, power : Int, target : Qubit[]
)
: Unit
is Adj + Ctl {
// The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We
// also use `ExpModI` to compute a by which x must be multiplied. Also
// note that we interpret target as unsigned integer in little-endian
// encoding.
ModularMultiplyByConstant(modulus,
ExpModI(generator, power, modulus),
target);
}
/// # Summary
/// Performs modular in-place multiplication by a classical constant.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(c*x) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular multiplication
/// ## c
/// Constant by which to multiply |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
use qs = Qubit[Length(y)];
for (idx, yq) in Enumerated(y) {
let shiftedC = (c <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, shiftedC, qs));
}
ApplyToEachCA(SWAP, Zipped(y, qs));
let invC = InverseModI(c, modulus);
for (idx, yq) in Enumerated(y) {
let shiftedC = (invC <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs));
}
}
/// # Summary
/// Performs modular in-place addition of a classical constant into a
/// quantum register.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(x+c) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular addition
/// ## c
/// Constant to add to |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
body (...) {
Controlled ModularAddConstant([], (modulus, c, y));
}
controlled (ctrls, ...) {
// We apply a custom strategy to control this operation instead of
// letting the compiler create the controlled variant for us in which
// the `Controlled` functor would be distributed over each operation
// in the body.
//
// Here we can use some scratch memory to save ensure that at most one
// control qubit is used for costly operations such as `AddConstant`
// and `CompareGreaterThenOrEqualConstant`.
if Length(ctrls) >= 2 {
use control = Qubit();
within {
Controlled X(ctrls, control);
} apply {
Controlled ModularAddConstant([control], (modulus, c, y));
}
} else {
use carry = Qubit();
Controlled AddConstant(ctrls, (c, y + [carry]));
Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry]));
Controlled AddConstant([carry], (modulus, y));
Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry));
}
}
}
/// # Summary
/// Performs in-place addition of a constant into a quantum register.
///
/// # Description
/// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive
/// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩.
///
/// # Input
/// ## c
/// Constant number to add to |𝑦⟩.
/// ## y
/// Quantum register of second summand and target; must not be empty.
internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl {
// We are using this version instead of the library version that is based
// on Fourier angles to show an advantage of sparse simulation in this sample.
let n = Length(y);
Fact(n > 0, "Bit width must be at least 1");
Fact(c >= 0, "constant must not be negative");
Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}");
if c != 0 {
// If c has j trailing zeroes than the j least significant bits
// of y won't be affected by the addition and can therefore be
// ignored by applying the addition only to the other qubits and
// shifting c accordingly.
let j = NTrailingZeroes(c);
use x = Qubit[n - j];
within {
ApplyXorInPlace(c >>> j, x);
} apply {
IncByLE(x, y[j...]);
}
}
}
/// # Summary
/// Performs greater-than-or-equals comparison to a constant.
///
/// # Description
/// Toggles output qubit `target` if and only if input register `x`
/// is greater than or equal to `c`.
///
/// # Input
/// ## c
/// Constant value for comparison.
/// ## x
/// Quantum register to compare against.
/// ## target
/// Target qubit for comparison result.
///
/// # Reference
/// This construction is described in [Lemma 3, arXiv:2201.10200]
internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit)
: Unit is Adj+Ctl {
let bitWidth = Length(x);
if c == 0 {
X(target);
} elif c >= 2 ^ bitWidth {
// do nothing
} elif c == 2 ^ (bitWidth - 1) {
ApplyLowTCNOT(Tail(x), target);
} else {
// normalize constant
let l = NTrailingZeroes(c);
let cNormalized = c >>> l;
let xNormalized = x[l...];
let bitWidthNormalized = Length(xNormalized);
let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized));
use qs = Qubit[bitWidthNormalized - 1];
let cs1 = [Head(xNormalized)] + Most(qs);
let cs2 = Rest(xNormalized);
within {
for i in IndexRange(gates) {
(gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]);
}
} apply {
ApplyLowTCNOT(Tail(qs), target);
}
}
}
/// # Summary
/// Internal operation used in the implementation of GreaterThanOrEqualConstant.
internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj {
within {
ApplyToEachA(X, [control1, control2]);
} apply {
ApplyAnd(control1, control2, target);
X(target);
}
}
internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit)
: Unit is Adj {
body (...) {
CCNOT(control1, control2, target);
}
adjoint (...) {
H(target);
if (M(target) == One) {
X(target);
CZ(control1, control2);
}
}
}
/// # Summary
/// Returns the number of trailing zeroes of a number
///
/// ## Example
/// ```qsharp
/// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0
/// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2
/// ```
internal function NTrailingZeroes(number : Int) : Int {
mutable nZeroes = 0;
mutable copy = number;
while (copy % 2 == 0) {
nZeroes += 1;
copy /= 2;
}
return nZeroes;
}
/// # Summary
/// An implementation for `CNOT` that when controlled using a single control uses
/// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7.
internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl {
body (...) {
CNOT(a, b);
}
adjoint self;
controlled (ctls, ...) {
// In this application this operation is used in a way that
// it is controlled by at most one qubit.
Fact(Length(ctls) <= 1, "At most one control line allowed");
if IsEmpty(ctls) {
CNOT(a, b);
} else {
use q = Qubit();
within {
ApplyAnd(Head(ctls), a, q);
} apply {
CNOT(q, b);
}
}
}
controlled adjoint self;
}
Uruchamianie narzędzia do szacowania zasobów
Narzędzie do szacowania zasobów oferuje sześć wstępnie zdefiniowanych parametrów kubitu, z których cztery mają zestawy instrukcji opartych na bramie i dwa, które mają zestaw instrukcji Majorana. Oferuje również dwa kwantowe kodysurface_code poprawek błędów i floquet_code.
W tym przykładzie uruchomisz narzędzie do szacowania zasobów przy użyciu parametru kubitu qubit_gate_us_e3 i kodu korekty błędu kwantowego surface_code .
Wybierz pozycję Widok —> paleta poleceń i wpisz ciąg "resource", który powinien wyświetlić opcję Q#: Oblicz szacunki zasobów. Możesz również kliknąć pozycję Szacowanie z listy poleceń wyświetlanych bezpośrednio przed operacją
Main. Wybierz tę opcję, aby otworzyć okno Narzędzie do szacowania zasobów.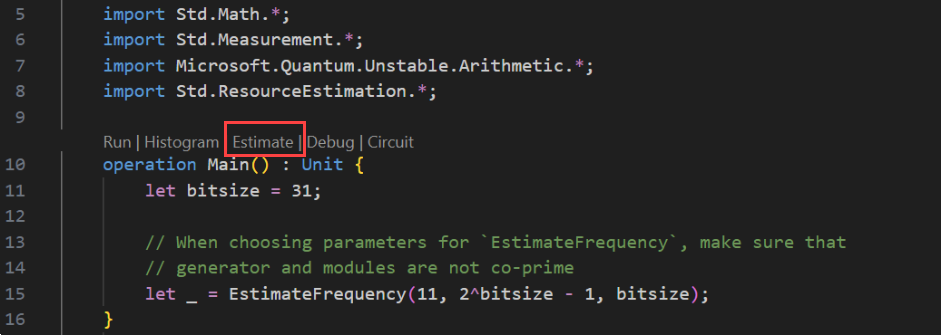
Aby oszacować zasoby, możesz wybrać co najmniej jeden parametr kubitu + typy kodów poprawek błędów. W tym przykładzie wybierz pozycję qubit_gate_us_e3 i kliknij przycisk OK.
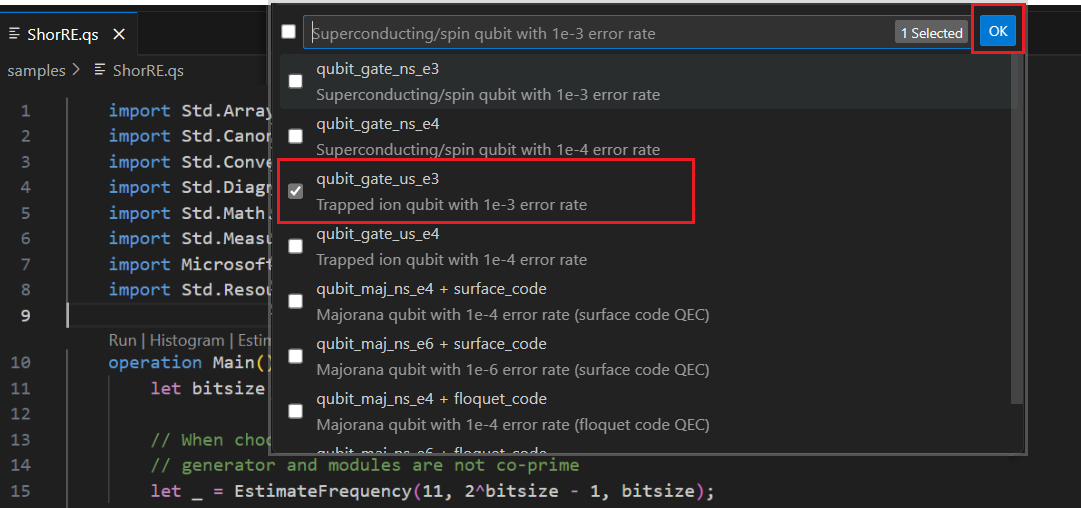
Określ budżet Błąd lub zaakceptuj wartość domyślną 0.001. W tym przykładzie pozostaw wartość domyślną i naciśnij Enter.
Naciśnij Enter , aby zaakceptować domyślną nazwę wyniku na podstawie nazwy pliku, w tym przypadku ShorRE.
Wyświetlanie wyników
Narzędzie do szacowania zasobów udostępnia wiele oszacowań dla tego samego algorytmu, z których każdy pokazuje kompromisy między liczbą kubitów a środowiskiem uruchomieniowym. Zrozumienie kompromisu między środowiskiem uruchomieniowym a skalowaniem systemu jest jednym z ważniejszych aspektów szacowania zasobów.
Wynik szacowania zasobów jest wyświetlany w oknie Szacowanie języka Q#.
Karta Wyniki zawiera podsumowanie szacowania zasobów. Kliknij ikonę obok pierwszego wiersza, aby wybrać kolumny, które chcesz wyświetlić. Możesz wybrać spośród nazw przebiegów, typu szacowania, typu kubitu, schematu qec, budżetu błędu, kubitów logicznych, głębokości logicznej, odległości kodu, stanów T, fabryk T, ułamka fabryki T, środowiska uruchomieniowego, rQOPS i kubitów fizycznych.
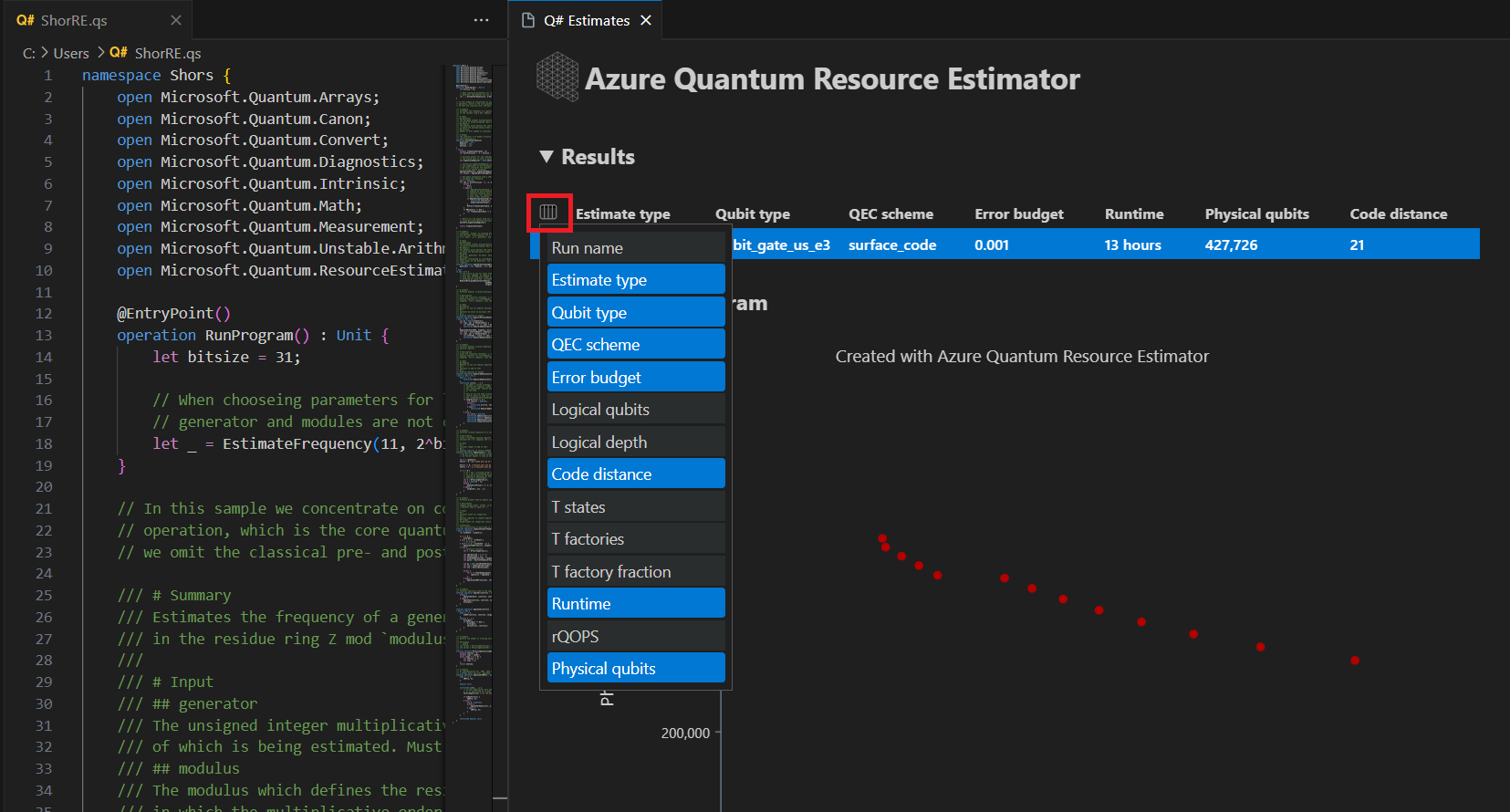
W kolumnie Szacowanie typu tabeli wyników można zobaczyć liczbę optymalnych kombinacji {liczba kubitów , środowisko uruchomieniowe} dla algorytmu. Te kombinacje można zobaczyć na diagramie czasu kosmicznego.
Diagram czasu kosmicznego przedstawia kompromisy między liczbą kubitów fizycznych a środowiskiem uruchomieniowym algorytmu. W tym przypadku narzędzie do szacowania zasobów znajduje 13 różnych optymalnych kombinacji z wielu tysięcy możliwych. Możesz umieścić wskaźnik myszy na poszczególnych {liczba kubitów, środowisko uruchomieniowe}, aby zobaczyć szczegóły szacowania zasobów w tym momencie.
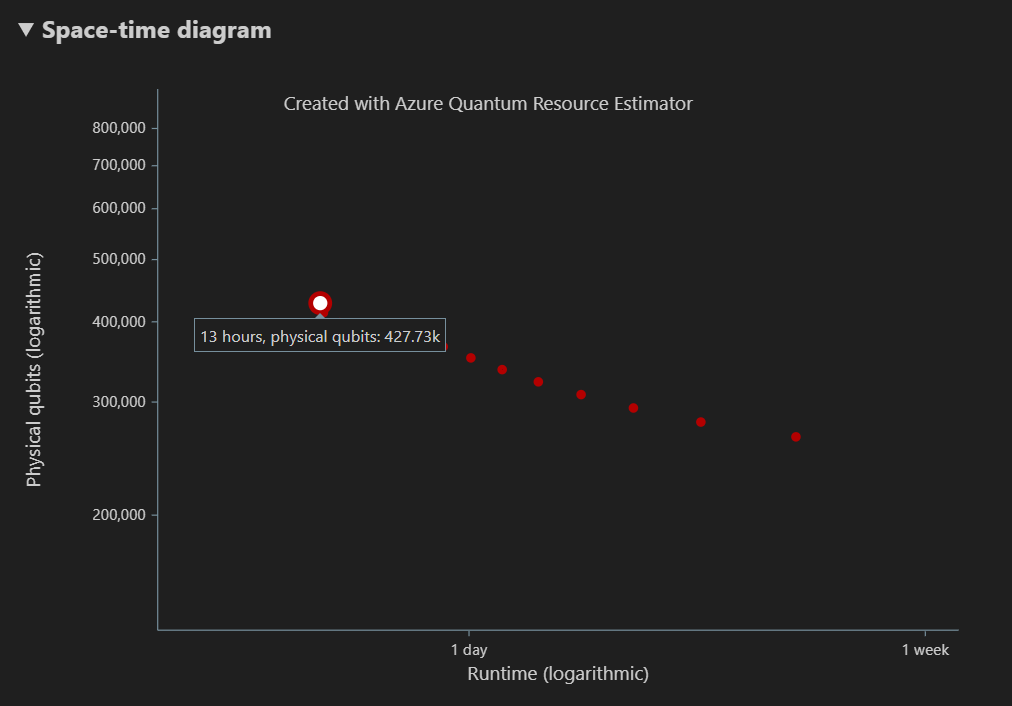
Aby uzyskać więcej informacji, zobacz Diagram czasu kosmicznego.
Uwaga
Musisz kliknąć jeden punkt diagramu czasu kosmicznego, czyli {liczba kubitów, czasu uruchomieniowego} w celu wyświetlenia diagramu przestrzeni i szczegółów szacowania zasobów odpowiadających temu punktowi.
Diagram kosmiczny przedstawia rozkład fizycznych kubitów używanych dla algorytmu i fabryk T odpowiadających {liczbie kubitów, czasu wykonania}. Jeśli na przykład wybierzesz najbardziej lewy punkt na diagramie czasu przestrzeni, liczba fizycznych kubitów wymaganych do uruchomienia algorytmu jest 427726, z których 196686 są kubitami algorytmów i 231040, z których są kubitami fabryki T.
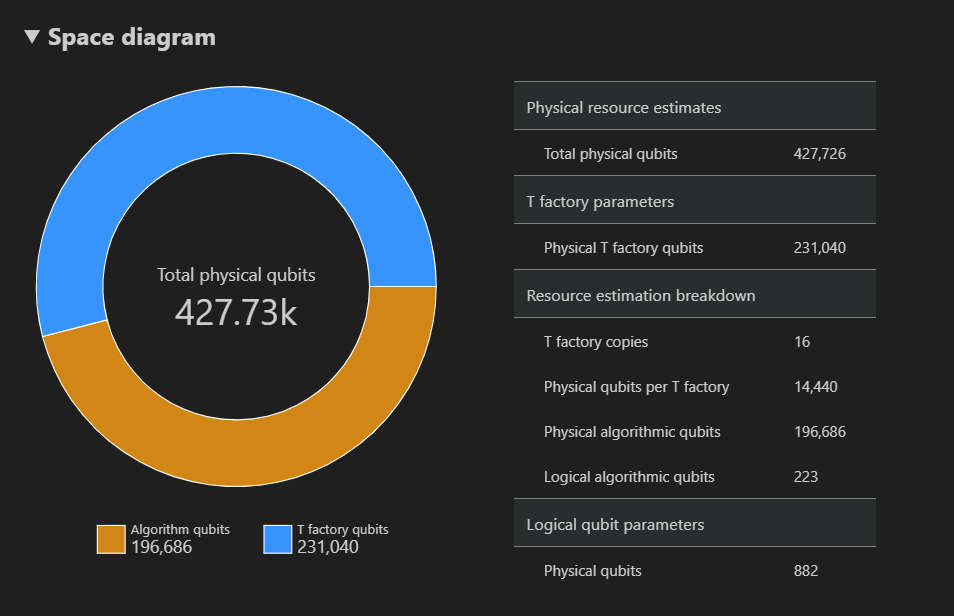
Na koniec na karcie Szacowanie zasobów zostanie wyświetlona pełna lista danych wyjściowych narzędzia do szacowania zasobów odpowiadająca parze {liczba kubitów, środowiska uruchomieniowego} . Szczegóły kosztów można sprawdzić, zwijając grupy, które zawierają więcej informacji. Na przykład wybierz najbardziej lewy punkt na diagramie czasu przestrzeni i zwiń grupę Parametrów kubitu logicznego.
Parametr kubitu logicznego Wartość Schemat QEC surface_code Odległość kodu 21 Kubity fizyczne 882 Czas cyklu logicznego 13 milisekund Szybkość błędów kubitu logicznego 3.00E-13 Wstępna przeprawa 0.03 Próg korekty błędu 0,01 Formuła czasu cyklu logicznego (4 * twoQubitGateTime+ 2 *oneQubitMeasurementTime) *codeDistanceFormuła kubitów fizycznych 2 * codeDistance*codeDistanceNapiwek
Kliknij pozycję Pokaż szczegółowe wiersze , aby wyświetlić opis poszczególnych danych wyjściowych danych raportu.
Aby uzyskać więcej informacji, zobacz pełne dane raportu narzędzia do szacowania zasobów.
Zmienianie parametrów target
Możesz oszacować koszt dla tego samego programu w języku Q# przy użyciu innego typu kubitu, kodu korekty błędów i budżetu błędu. Otwórz okno Narzędzie do szacowania zasobów, wybierając pozycję Widok —> Paleta poleceń i wpisz Q#: Calculate Resource Estimates.
Wybierz dowolną inną konfigurację, na przykład parametr kubitu opartego na majoranie, qubit_maj_ns_e6. Zaakceptuj domyślną wartość budżetu błędu lub wprowadź nową, a następnie naciśnij Enter. Narzędzie do szacowania zasobów ponownie uruchamia szacowanie przy użyciu nowych target parametrów.
Aby uzyskać więcej informacji, zobacz Target parametry narzędzia do szacowania zasobów.
Uruchamianie wielu konfiguracji parametrów
Narzędzie do szacowania zasobów usługi Azure Quantum może uruchamiać wiele konfiguracji parametrów target i porównywać wyniki szacowania zasobów.
Wybierz pozycję Widok —> Paleta poleceń lub naciśnij Ctrl+Shift+P i wpisz
Q#: Calculate Resource Estimatespolecenie .Wybierz qubit_gate_us_e3, qubit_gate_us_e4, qubit_maj_ns_e4 + floquet_code i qubit_maj_ns_e6 + floquet_code, a następnie kliknij przycisk OK.
Zaakceptuj domyślną wartość budżetu błędu 0.001 i naciśnij Enter.
Naciśnij Enter , aby zaakceptować plik wejściowy, w tym przypadku ShorRE.qs.
W przypadku wielu konfiguracji parametrów wyniki są wyświetlane w różnych wierszach na karcie Wyniki .
Diagram czasu przestrzeni przedstawia wyniki dla wszystkich konfiguracji parametrów. Pierwsza kolumna tabeli wyników zawiera legendę dla każdej konfiguracji parametrów. Możesz zatrzymać wskaźnik myszy na każdym punkcie, aby zobaczyć szczegóły szacowania zasobów w tym momencie.
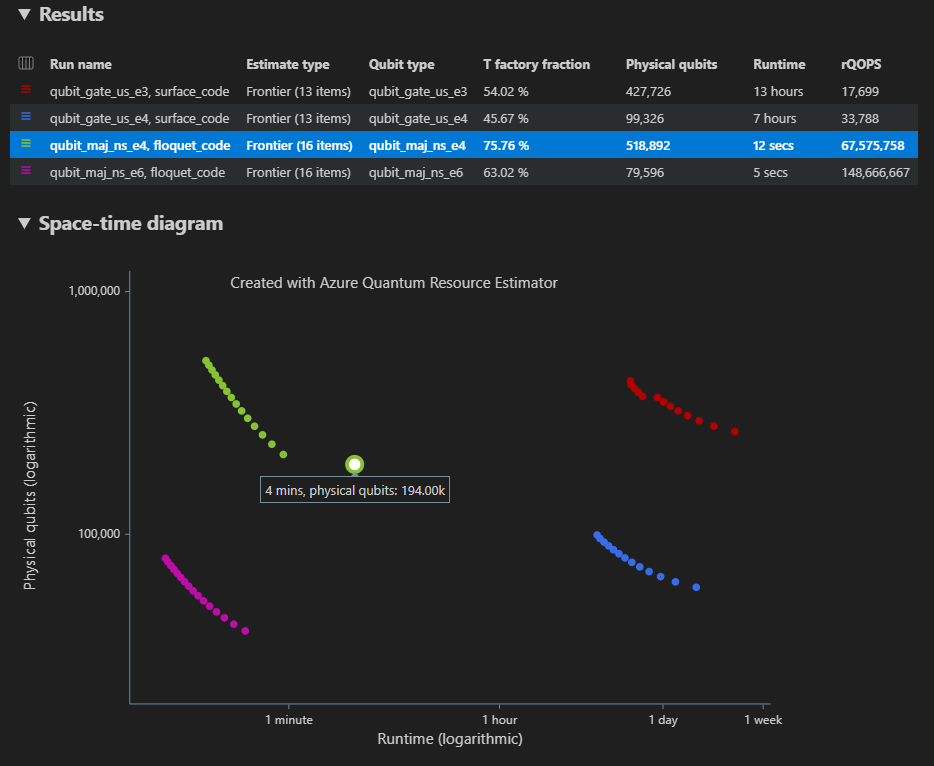
Kliknij {liczbę kubitów, punkt środowiska uruchomieniowego} diagramu czasu kosmicznego, aby wyświetlić odpowiedni diagram przestrzeni i dane raportu.
Wymagania wstępne dotyczące notesu Jupyter w programie VS Code
Środowisko języka Python z zainstalowanym językiem Python i programem .
Najnowsza wersja programu Visual Studio Code lub otwórz program VS Code w sieci Web.
Program VS Code z zainstalowanymi rozszerzeniami Quantum Development Kit, Pythoni jupyter.
Najnowsze pakiety i
qsharpusługi Azure Quantumqsharp_widgets.python -m pip install --upgrade qsharp qsharp_widgetslub
!pip install --upgrade qsharp qsharp_widgets
Napiwek
Nie musisz mieć konta platformy Azure, aby uruchomić narzędzie do szacowania zasobów.
Tworzenie algorytmu kwantowego
W programie VS Code wybierz pozycję > poleceń i wybierz pozycję Utwórz: nowy notes Jupyter.
W prawym górnym rogu program VS Code wykryje i wyświetli wersję języka Python oraz wirtualne środowisko języka Python wybrane dla notesu. Jeśli masz wiele środowisk języka Python, może być konieczne wybranie jądra przy użyciu selektora jądra w prawym górnym rogu. Jeśli środowisko nie zostało wykryte, zobacz Jupyter Notebooks in VS Code (Notesy Jupyter Notebooks w programie VS Code ), aby uzyskać informacje o konfiguracji.
W pierwszej komórce notesu zaimportuj
qsharppakiet.import qsharpDodaj nową komórkę i skopiuj następujący kod.
%%qsharp import Std.Arrays.*; import Std.Canon.*; import Std.Convert.*; import Std.Diagnostics.*; import Std.Math.*; import Std.Measurement.*; import Microsoft.Quantum.Unstable.Arithmetic.*; import Std.ResourceEstimation.*; operation RunProgram() : Unit { let bitsize = 31; // When choosing parameters for `EstimateFrequency`, make sure that // generator and modules are not co-prime let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize); } // In this sample we concentrate on costing the `EstimateFrequency` // operation, which is the core quantum operation in Shors algorithm, and // we omit the classical pre- and post-processing. /// # Summary /// Estimates the frequency of a generator /// in the residue ring Z mod `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order (period) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## bitsize /// Number of bits needed to represent the modulus. /// /// # Output /// The numerator k of dyadic fraction k/2^bitsPrecision /// approximating s/r. operation EstimateFrequency( generator : Int, modulus : Int, bitsize : Int ) : Int { mutable frequencyEstimate = 0; let bitsPrecision = 2 * bitsize + 1; // Allocate qubits for the superposition of eigenstates of // the oracle that is used in period finding. use eigenstateRegister = Qubit[bitsize]; // Initialize eigenstateRegister to 1, which is a superposition of // the eigenstates we are estimating the phases of. // We first interpret the register as encoding an unsigned integer // in little endian encoding. ApplyXorInPlace(1, eigenstateRegister); let oracle = ApplyOrderFindingOracle(generator, modulus, _, _); // Use phase estimation with a semiclassical Fourier transform to // estimate the frequency. use c = Qubit(); for idx in bitsPrecision - 1..-1..0 { within { H(c); } apply { // `BeginEstimateCaching` and `EndEstimateCaching` are the operations // exposed by Azure Quantum Resource Estimator. These will instruct // resource counting such that the if-block will be executed // only once, its resources will be cached, and appended in // every other iteration. if BeginEstimateCaching("ControlledOracle", SingleVariant()) { Controlled oracle([c], (1 <<< idx, eigenstateRegister)); EndEstimateCaching(); } R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c); } if MResetZ(c) == One { frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx); } } // Return all the qubits used for oracle eigenstate back to 0 state // using Microsoft.Quantum.Intrinsic.ResetAll. ResetAll(eigenstateRegister); return frequencyEstimate; } /// # Summary /// Interprets `target` as encoding unsigned little-endian integer k /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where /// p is `power`, g is `generator` and N is `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order ( period ) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## power /// Power of `generator` by which `target` is multiplied. /// ## target /// Register interpreted as little endian encoded which is multiplied by /// given power of the generator. The multiplication is performed modulo /// `modulus`. internal operation ApplyOrderFindingOracle( generator : Int, modulus : Int, power : Int, target : Qubit[] ) : Unit is Adj + Ctl { // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We // also use `ExpModI` to compute a by which x must be multiplied. Also // note that we interpret target as unsigned integer in little-endian // encoding. ModularMultiplyByConstant(modulus, ExpModI(generator, power, modulus), target); } /// # Summary /// Performs modular in-place multiplication by a classical constant. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(c*x) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular multiplication /// ## c /// Constant by which to multiply |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { use qs = Qubit[Length(y)]; for (idx, yq) in Enumerated(y) { let shiftedC = (c <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, shiftedC, qs)); } ApplyToEachCA(SWAP, Zipped(y, qs)); let invC = InverseModI(c, modulus); for (idx, yq) in Enumerated(y) { let shiftedC = (invC <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs)); } } /// # Summary /// Performs modular in-place addition of a classical constant into a /// quantum register. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(x+c) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular addition /// ## c /// Constant to add to |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { body (...) { Controlled ModularAddConstant([], (modulus, c, y)); } controlled (ctrls, ...) { // We apply a custom strategy to control this operation instead of // letting the compiler create the controlled variant for us in which // the `Controlled` functor would be distributed over each operation // in the body. // // Here we can use some scratch memory to save ensure that at most one // control qubit is used for costly operations such as `AddConstant` // and `CompareGreaterThenOrEqualConstant`. if Length(ctrls) >= 2 { use control = Qubit(); within { Controlled X(ctrls, control); } apply { Controlled ModularAddConstant([control], (modulus, c, y)); } } else { use carry = Qubit(); Controlled AddConstant(ctrls, (c, y + [carry])); Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry])); Controlled AddConstant([carry], (modulus, y)); Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry)); } } } /// # Summary /// Performs in-place addition of a constant into a quantum register. /// /// # Description /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩. /// /// # Input /// ## c /// Constant number to add to |𝑦⟩. /// ## y /// Quantum register of second summand and target; must not be empty. internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl { // We are using this version instead of the library version that is based // on Fourier angles to show an advantage of sparse simulation in this sample. let n = Length(y); Fact(n > 0, "Bit width must be at least 1"); Fact(c >= 0, "constant must not be negative"); Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}"); if c != 0 { // If c has j trailing zeroes than the j least significant bits // of y will not be affected by the addition and can therefore be // ignored by applying the addition only to the other qubits and // shifting c accordingly. let j = NTrailingZeroes(c); use x = Qubit[n - j]; within { ApplyXorInPlace(c >>> j, x); } apply { IncByLE(x, y[j...]); } } } /// # Summary /// Performs greater-than-or-equals comparison to a constant. /// /// # Description /// Toggles output qubit `target` if and only if input register `x` /// is greater than or equal to `c`. /// /// # Input /// ## c /// Constant value for comparison. /// ## x /// Quantum register to compare against. /// ## target /// Target qubit for comparison result. /// /// # Reference /// This construction is described in [Lemma 3, arXiv:2201.10200] internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit) : Unit is Adj+Ctl { let bitWidth = Length(x); if c == 0 { X(target); } elif c >= 2 ^ bitWidth { // do nothing } elif c == 2 ^ (bitWidth - 1) { ApplyLowTCNOT(Tail(x), target); } else { // normalize constant let l = NTrailingZeroes(c); let cNormalized = c >>> l; let xNormalized = x[l...]; let bitWidthNormalized = Length(xNormalized); let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized)); use qs = Qubit[bitWidthNormalized - 1]; let cs1 = [Head(xNormalized)] + Most(qs); let cs2 = Rest(xNormalized); within { for i in IndexRange(gates) { (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]); } } apply { ApplyLowTCNOT(Tail(qs), target); } } } /// # Summary /// Internal operation used in the implementation of GreaterThanOrEqualConstant. internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { within { ApplyToEachA(X, [control1, control2]); } apply { ApplyAnd(control1, control2, target); X(target); } } internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { body (...) { CCNOT(control1, control2, target); } adjoint (...) { H(target); if (M(target) == One) { X(target); CZ(control1, control2); } } } /// # Summary /// Returns the number of trailing zeroes of a number /// /// ## Example /// ```qsharp /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0 /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2 /// ``` internal function NTrailingZeroes(number : Int) : Int { mutable nZeroes = 0; mutable copy = number; while (copy % 2 == 0) { nZeroes += 1; copy /= 2; } return nZeroes; } /// # Summary /// An implementation for `CNOT` that when controlled using a single control uses /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7. internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl { body (...) { CNOT(a, b); } adjoint self; controlled (ctls, ...) { // In this application this operation is used in a way that // it is controlled by at most one qubit. Fact(Length(ctls) <= 1, "At most one control line allowed"); if IsEmpty(ctls) { CNOT(a, b); } else { use q = Qubit(); within { ApplyAnd(Head(ctls), a, q); } apply { CNOT(q, b); } } } controlled adjoint self; }
Szacowanie algorytmu kwantowego
Teraz szacujesz zasoby fizyczne dla RunProgram operacji przy użyciu domyślnych założeń. Dodaj nową komórkę i skopiuj następujący kod.
result = qsharp.estimate("RunProgram()")
result
Funkcja qsharp.estimate tworzy obiekt wynikowy, który może służyć do wyświetlania tabeli z ogólną liczbą zasobów fizycznych. Szczegóły kosztów można sprawdzić, rozwijając grupy, które zawierają więcej informacji. Aby uzyskać więcej informacji, zobacz pełne dane raportu narzędzia do szacowania zasobów.
Na przykład rozwiń grupę parametrów kubitu logicznego , aby zobaczyć, że odległość kodu wynosi 21, a liczba kubitów fizycznych wynosi 882.
| Parametr kubitu logicznego | Wartość |
|---|---|
| Schemat QEC | surface_code |
| Odległość kodu | 21 |
| Kubity fizyczne | 882 |
| Czas cyklu logicznego | 8 milisekund |
| Szybkość błędów kubitu logicznego | 3.00E-13 |
| Wstępna przeprawa | 0.03 |
| Próg korekty błędu | 0,01 |
| Formuła czasu cyklu logicznego | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Formuła kubitów fizycznych | 2 * codeDistance * codeDistance |
Napiwek
W przypadku bardziej kompaktowej wersji tabeli wyjściowej można użyć polecenia result.summary.
Diagram przestrzeni
Rozkład fizycznych kubitów używanych dla algorytmu i fabryk T jest czynnikiem, który może mieć wpływ na projekt algorytmu. Pakiet umożliwia qsharp-widgets wizualizowanie tej dystrybucji w celu lepszego zrozumienia szacowanych wymagań dotyczących miejsca dla algorytmu.
from qsharp-widgets import SpaceChart, EstimateDetails
SpaceChart(result)
W tym przykładzie liczba fizycznych kubitów wymaganych do uruchomienia algorytmu jest 829766, z których 196686 są kubitami algorytmów i 633080, z których są kubitami fabryki T.
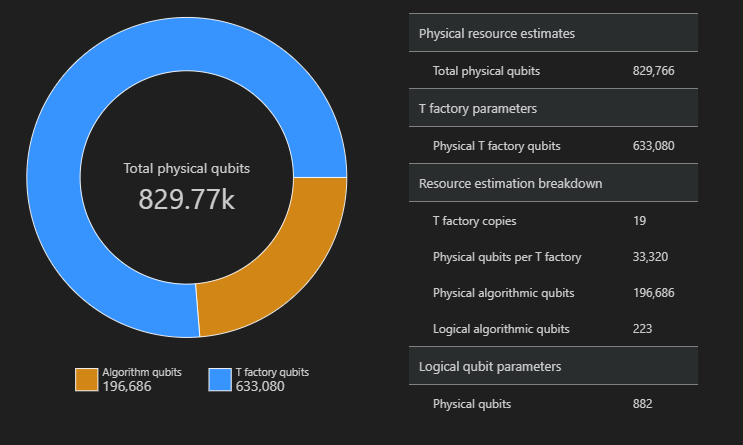
Zmienianie wartości domyślnych i szacowanie algorytmu
Podczas przesyłania żądania szacowania zasobów dla programu można określić niektóre parametry opcjonalne.
jobParams Użyj pola, aby uzyskać dostęp do wszystkich target parametrów, które można przekazać do wykonania zadania i sprawdzić, które wartości domyślne zostały przyjęte:
result['jobParams']
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
Widać, że narzędzie do szacowania zasobów przyjmuje model kubitu qubit_gate_ns_e3 , surface_code kod korekty błędu i budżet błędu 0,001 jako wartości domyślne szacowania.
target Są to parametry, które można dostosować:
-
errorBudget— ogólny dozwolony budżet błędów dla algorytmu -
qecScheme- schemat poprawki błędów kwantowych (QEC) -
qubitParams- parametry kubitu fizycznego -
constraints- ograniczenia na poziomie składników -
distillationUnitSpecifications- specyfikacje algorytmów destylowania fabryk T -
estimateType- pojedyncza lub granica
Aby uzyskać więcej informacji, zobacz Target parametry narzędzia do szacowania zasobów.
Zmienianie modelu kubitu
Koszt dla tego samego algorytmu można oszacować przy użyciu parametru kubitu opartego na majoranie , qubitParams"qubit_maj_ns_e6".
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
}})
EstimateDetails(result_maj)
Zmienianie schematu korekty błędów kwantowych
Możesz ponownie uruchomić zadanie szacowania zasobów dla tego samego przykładu na podstawie parametrów kubitu opartego na Majorana ze schematem qecSchemeQEC floqued.
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
}})
EstimateDetails(result_maj)
Zmiana budżetu błędu
Następnie ponownie uruchom ten sam obwód kwantowy z wartością errorBudget 10%.
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
},
"errorBudget": 0.1})
EstimateDetails(result_maj)
Przetwarzanie wsadowe za pomocą narzędzia do szacowania zasobów
Narzędzie do szacowania zasobów usługi Azure Quantum umożliwia uruchamianie wielu konfiguracji parametrów target i porównywanie wyników. Jest to przydatne, gdy chcesz porównać koszt różnych modeli kubitów, schematów QEC lub budżetów błędów.
Szacowanie wsadowe można wykonać, przekazując listę parametrów target do
paramsparametruqsharp.estimatefunkcji. Na przykład uruchom ten sam algorytm z parametrami domyślnymi i parametrami kubitu opartymi na majoranie ze schematem QEC floquet.result_batch = qsharp.estimate("RunProgram()", params= [{}, # Default parameters { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" } }]) result_batch.summary_data_frame(labels=["Gate-based ns, 10⁻³", "Majorana ns, 10⁻⁶"])Model Kubity logiczne Głębokość logiczna Stany T Odległość kodu Fabryki T Ułamek fabryki T Kubity fizyczne rQOPS Środowisko uruchomieniowe fizyczne Ns oparte na bramie, 10⁻³ 223 3,64 mln 4,70 mln 21 19 76.30 % 829,77 tys. 26,55 mln 31 s Majorana ns, 10⁻⁶ 223 3,64 mln 4,70 mln 5 19 63.02 % 79,60 tys. 148,67 mln 5 s Możesz również utworzyć listę parametrów szacowania przy użyciu
EstimatorParamsklasy .from qsharp.estimator import EstimatorParams, QubitParams, QECScheme, LogicalCounts labels = ["Gate-based µs, 10⁻³", "Gate-based µs, 10⁻⁴", "Gate-based ns, 10⁻³", "Gate-based ns, 10⁻⁴", "Majorana ns, 10⁻⁴", "Majorana ns, 10⁻⁶"] params = EstimatorParams(num_items=6) params.error_budget = 0.333 params.items[0].qubit_params.name = QubitParams.GATE_US_E3 params.items[1].qubit_params.name = QubitParams.GATE_US_E4 params.items[2].qubit_params.name = QubitParams.GATE_NS_E3 params.items[3].qubit_params.name = QubitParams.GATE_NS_E4 params.items[4].qubit_params.name = QubitParams.MAJ_NS_E4 params.items[4].qec_scheme.name = QECScheme.FLOQUET_CODE params.items[5].qubit_params.name = QubitParams.MAJ_NS_E6 params.items[5].qec_scheme.name = QECScheme.FLOQUET_CODEqsharp.estimate("RunProgram()", params=params).summary_data_frame(labels=labels)Model Kubity logiczne Głębokość logiczna Stany T Odległość kodu Fabryki T Ułamek fabryki T Kubity fizyczne rQOPS Środowisko uruchomieniowe fizyczne Oparte na bramie μs, 10⁻³ 223 3,64 mln 4,70 mln 17 13 40.54 % 216,77 tys. 21,86 tys. 10 godzin Oparte na bramie μs, 10⁻⁴ 223 3,64 mln 4,70 mln 9 14 43.17 % 63,57 tys. 41,30 tys. 5 godzin Ns oparte na bramie, 10⁻³ 223 3,64 mln 4,70 mln 17 16 69.08 % 416.89k 32,79 mln 25 s Ns oparte na bramie, 10⁻⁴ 223 3,64 mln 4,70 mln 9 14 43.17 % 63,57 tys. 61,94 mln 13 s Majorana ns, 10⁻⁴ 223 3,64 mln 4,70 mln 9 19 82.75 % 501.48k 82,59 mln 10 sekund Majorana ns, 10⁻⁶ 223 3,64 mln 4,70 mln 5 13 31.47 % 42,96 tys. 148,67 mln 5 s
Uruchamianie szacowania granic Pareto
Podczas szacowania zasobów algorytmu należy wziąć pod uwagę kompromis między liczbą kubitów fizycznych a środowiskiem uruchomieniowym algorytmu. Możesz rozważyć alokację jak największej liczby kubitów fizycznych, aby zmniejszyć środowisko uruchomieniowe algorytmu. Jednak liczba kubitów fizycznych jest ograniczona przez liczbę kubitów fizycznych dostępnych na sprzęcie kwantowym.
Szacowanie granic Pareto zapewnia wiele oszacowań dla tego samego algorytmu, z których każdy ma kompromis między liczbą kubitów a środowiskiem uruchomieniowym.
Aby uruchomić narzędzie do szacowania zasobów przy użyciu szacowania granic Pareto, należy określić
"estimateType"target parametr jako"frontier". Na przykład uruchom ten sam algorytm z parametrami kubitu opartymi na majoranie z kodem powierzchni przy użyciu szacowania granic Pareto.result = qsharp.estimate("RunProgram()", params= {"qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # frontier estimation } )Za pomocą
EstimatesOverviewfunkcji można wyświetlić tabelę z ogólnymi liczbami zasobów fizycznych. Kliknij ikonę obok pierwszego wiersza, aby wybrać kolumny, które chcesz wyświetlić. Możesz wybrać spośród nazw przebiegów, typu szacowania, typu kubitu, schematu qec, budżetu błędu, kubitów logicznych, głębokości logicznej, odległości kodu, stanów T, fabryk T, ułamka fabryki T, środowiska uruchomieniowego, rQOPS i kubitów fizycznych.from qsharp_widgets import EstimatesOverview EstimatesOverview(result)
W kolumnie Szacowanie typu tabeli wyników można zobaczyć liczbę różnych kombinacji {liczba kubitów, środowisko uruchomieniowe} dla algorytmu. W tym przypadku narzędzie do szacowania zasobów znajduje 22 różne optymalne kombinacje spośród wielu tysięcy możliwych.
Diagram czasu kosmicznego
Funkcja EstimatesOverview wyświetla również diagram czasu kosmicznego narzędzia do szacowania zasobów.
Diagram czasu kosmicznego przedstawia liczbę fizycznych kubitów i środowisko uruchomieniowe algorytmu dla każdej pary {liczba kubitów, środowiska uruchomieniowego}. Możesz zatrzymać wskaźnik myszy na każdym punkcie, aby zobaczyć szczegóły szacowania zasobów w tym momencie.
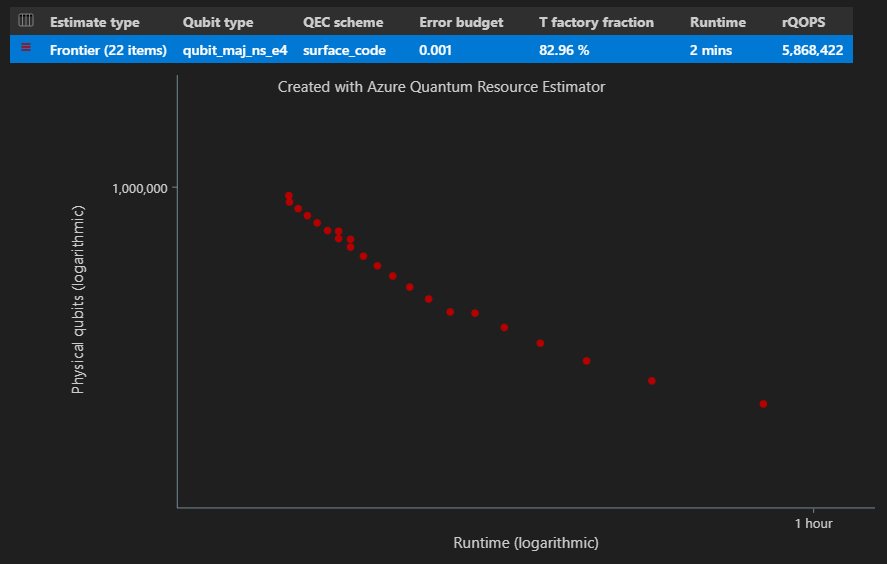
Dzielenie na partie przy użyciu szacowania granic Pareto
Aby oszacować i porównać wiele konfiguracji parametrów target z szacowaniem granic, dodaj
"estimateType": "frontier",do parametrów.result = qsharp.estimate( "RunProgram()", [ { "qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # Pareto frontier estimation }, { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" }, "estimateType": "frontier", # Pareto frontier estimation }, ] ) EstimatesOverview(result, colors=["#1f77b4", "#ff7f0e"], runNames=["e4 Surface Code", "e6 Floquet Code"])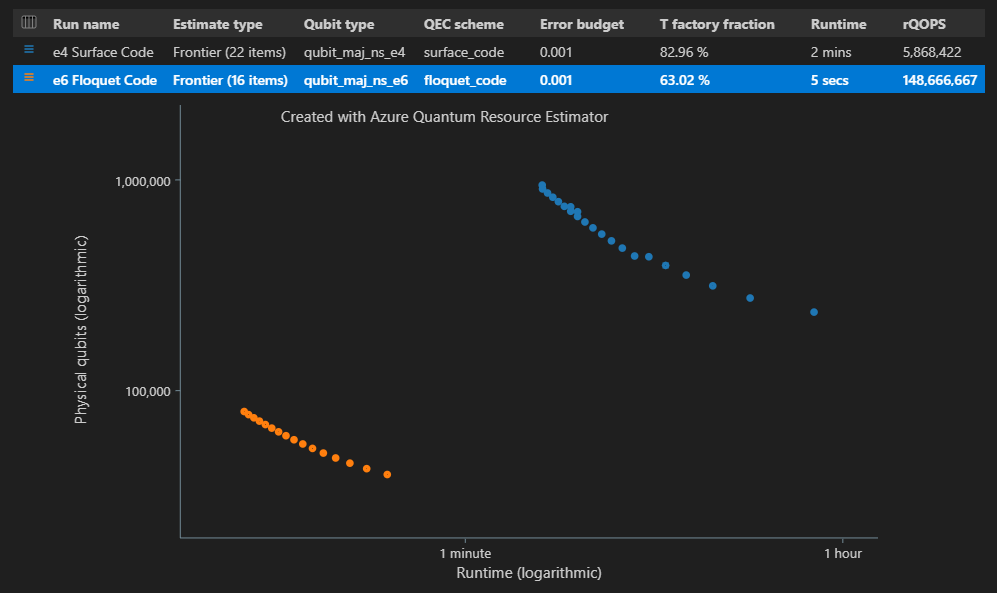
Uwaga
Za pomocą funkcji można definiować kolory i nazwy przebiegów diagramu czasu kubitu
EstimatesOverview.Podczas uruchamiania wielu konfiguracji parametrów target przy użyciu szacowania granic Pareto można zobaczyć oszacowania zasobów dla określonego punktu diagramu czasu przestrzeni, czyli dla każdej pary {liczba kubitów, runtime}. Na przykład poniższy kod przedstawia szacowane użycie szczegółów dla drugiego uruchomienia (estimate index=0) i czwartego (point index=3) najkrótszego środowiska uruchomieniowego.
EstimateDetails(result[1], 4)Można również zobaczyć diagram kosmiczny dla określonego punktu diagramu czasu kosmicznego. Na przykład poniższy kod przedstawia diagram przestrzeni dla pierwszego przebiegu kombinacji (szacowanie indeksu=0) i trzeciego najkrótszego środowiska uruchomieniowego (point index=2).
SpaceChart(result[0], 2)
Wymagania wstępne dla Qiskit w VS Code
Środowisko języka Python z zainstalowanym językiem Python i programem .
Najnowsza wersja programu Visual Studio Code lub otwórz Visual Studio Code w przeglądarce internetowej.
Program VS Code z zainstalowanymi rozszerzeniami Quantum Development Kit, Pythoni jupyter.
Najnowsze pakiety usługi Azure Quantum
qsharpiqsharp_widgetsorazqiskit.python -m pip install --upgrade qsharp qsharp_widgets qiskitlub
!pip install --upgrade qsharp qsharp_widgets qiskit
Napiwek
Nie musisz mieć konta platformy Azure, aby uruchomić narzędzie do szacowania zasobów.
Utwórz nowy notatnik Jupyter
- W programie VS Code wybierz pozycję > poleceń i wybierz pozycję Utwórz: nowy notes Jupyter.
- W prawym górnym rogu program VS Code wykryje i wyświetli wersję języka Python oraz wirtualne środowisko języka Python wybrane dla notesu. Jeśli masz wiele środowisk języka Python, może być konieczne wybranie jądra przy użyciu selektora jądra w prawym górnym rogu. Jeśli środowisko nie zostało wykryte, zobacz Jupyter Notebooks in VS Code (Notesy Jupyter Notebooks w programie VS Code ), aby uzyskać informacje o konfiguracji.
Tworzenie algorytmu kwantowego
W tym przykładzie utworzysz obwód kwantowy dla mnożnika na podstawie konstrukcji przedstawionej w ruiz-Perez i Garcia-Escartin (arXiv:1411.5949), która używa przekształcenia Quantum Fourier do implementowania arytmetyki.
Rozmiar mnożnika można dostosować, zmieniając zmienną bitwidth . Generowanie obwodu jest opakowane w funkcję, którą można wywołać przy bitwidth użyciu wartości mnożnika. Operacja będzie zawierać dwa rejestry wejściowe, każdy rozmiar określonego bitwidthi jeden rejestr wyjściowy, który jest dwa razy większy niż określony bitwidth. Funkcja wyświetli również niektóre liczby zasobów logicznych dla mnożnika wyodrębnionego bezpośrednio z obwodu kwantowego.
from qiskit.circuit.library import RGQFTMultiplier
def create_algorithm(bitwidth):
print(f"[INFO] Create a QFT-based multiplier with bitwidth {bitwidth}")
circ = RGQFTMultiplier(num_state_qubits=bitwidth)
return circ
Uwaga
Jeśli wybierzesz jądro języka Python, a moduł qiskit nie zostanie rozpoznany, spróbuj wybrać inne środowisko języka Python w selektorze jądra.
Szacowanie algorytmu kwantowego
Utwórz wystąpienie algorytmu create_algorithm przy użyciu funkcji . Rozmiar mnożnika można dostosować, zmieniając zmienną bitwidth .
bitwidth = 4
circ = create_algorithm(bitwidth)
Szacuj zasoby fizyczne dla tej operacji przy użyciu domyślnych założeń. Możesz użyć wywołania estimate, które jest przeciążone, aby zaakceptować obiekt QuantumCircuit z Qiskit.
from qsharp.estimator import EstimatorParams
from qsharp.interop.qiskit import estimate
params = EstimatorParams()
result = estimate(circ, params)
Alternatywnie możesz użyć ResourceEstimatorBackend, aby wykonać szacowanie, jak działa istniejące zaplecze.
from qsharp.interop.qiskit import ResourceEstimatorBackend
from qsharp.estimator import EstimatorParams
params = EstimatorParams()
backend = ResourceEstimatorBackend()
job = backend.run(circ, params)
result = job.result()
Obiekt result zawiera dane wyjściowe zadania szacowania zasobów. Możesz użyć funkcji EstimateDetails, aby wyświetlić wyniki w bardziej czytelnym formacie.
from qsharp_widgets import EstimateDetails
EstimateDetails(result)
EstimateDetails funkcja wyświetla tabelę z ogólnymi liczbami zasobów fizycznych. Szczegóły kosztów można sprawdzić, rozwijając grupy, które zawierają więcej informacji. Aby uzyskać więcej informacji, zobacz pełne dane raportu narzędzia do szacowania zasobów.
Na przykład, jeśli rozszerzysz grupę parametrów logicznych kubitu, możesz łatwiej dostrzec, że odległość kodu korekcji błędów wynosi 15.
| Parametr kubitu logicznego | Wartość |
|---|---|
| Schemat QEC | surface_code |
| Odległość kodu | 15 |
| Kubity fizyczne | 450 |
| Czas cyklu logicznego | 6us |
| Szybkość błędów kubitu logicznego | 3.00E-10 |
| Wstępna przeprawa | 0.03 |
| Próg korekty błędu | 0,01 |
| Formuła czasu cyklu logicznego | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Formuła kubitów fizycznych | 2 * codeDistance * codeDistance |
W grupie Parametry kubitu fizycznego można zobaczyć fizyczne właściwości kubitu, które zostały przyjęte dla tego oszacowania. Na przykład czas wykonywania pomiaru pojedynczego kubitu i bramki z jednym kubitem przyjmuje się odpowiednio 100 ns i 50 ns.
Napiwek
Możesz również uzyskać dostęp do danych wyjściowych narzędzia do szacowania zasobów jako słownika języka Python przy użyciu metody result.data(). Aby na przykład uzyskać dostęp do fizycznych ilości result.data()["physicalCounts"].
Diagramy przestrzeni
Rozkład fizycznych kubitów używanych dla algorytmu i fabryk T jest czynnikiem, który może mieć wpływ na projekt algorytmu. Możesz zwizualizować tę dystrybucję, aby lepiej zrozumieć szacowane wymagania dotyczące miejsca dla algorytmu.
from qsharp_widgets import SpaceChart
SpaceChart(result)
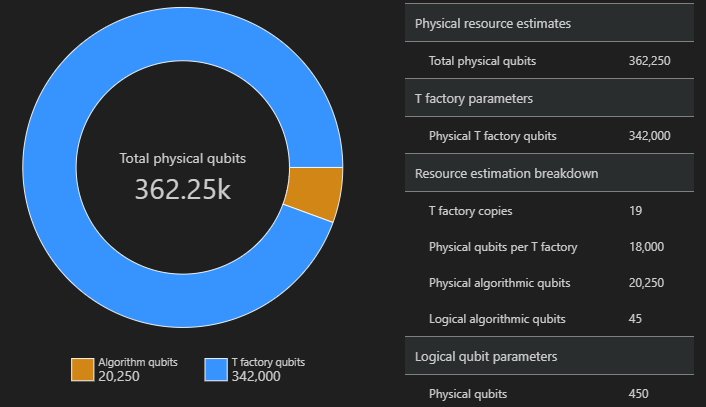
Diagram kosmiczny przedstawia proporcję kubitów algorytmu i kubitów fabrycznych T. Należy pamiętać, że liczba kopii fabrycznych T, 19, przyczynia się do liczby fizycznych kubitów fabryk T jako $\text{fabryk T} \cdot \text{fizyczny kubit na fabrykę T}= 19 \cdot 18.000 = 342.000$.
Aby uzyskać więcej informacji, zobacz Szacowanie fizyczne fabryki T.
Zmienianie wartości domyślnych i szacowanie algorytmu
Podczas przesyłania żądania szacowania zasobów dla programu można określić niektóre parametry opcjonalne.
jobParams Użyj pola, aby uzyskać dostęp do wszystkich wartości, które można przekazać do wykonania zadania i sprawdzić, które wartości domyślne zostały przyjęte:
result.data()["jobParams"]
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
target Są to parametry, które można dostosować:
-
errorBudget- ogólny dozwolony budżet błędów -
qecScheme- schemat poprawki błędów kwantowych (QEC) -
qubitParams- parametry kubitu fizycznego -
constraints- ograniczenia na poziomie składników -
distillationUnitSpecifications- specyfikacje algorytmów destylowania fabryk T
Aby uzyskać więcej informacji, zobacz Target parametry narzędzia do szacowania zasobów.
Zmienianie modelu kubitu
Następnie szacuj koszt dla tego samego algorytmu przy użyciu parametru kubitu opartego na majoranie qubit_maj_ns_e6
qubitParams = {
"name": "qubit_maj_ns_e6"
}
result = backend.run(circ, qubitParams).result()
Liczbę fizycznych można sprawdzić programowo. Możesz na przykład zapoznać się ze szczegółowymi informacjami na temat fabryki T, która została utworzona w celu wykonania algorytmu.
result.data()["tfactory"]
{'eccDistancePerRound': [1, 1, 5],
'logicalErrorRate': 1.6833177305222897e-10,
'moduleNamePerRound': ['15-to-1 space efficient physical',
'15-to-1 RM prep physical',
'15-to-1 RM prep logical'],
'numInputTstates': 20520,
'numModulesPerRound': [1368, 20, 1],
'numRounds': 3,
'numTstates': 1,
'physicalQubits': 16416,
'physicalQubitsPerRound': [12, 31, 1550],
'runtime': 116900.0,
'runtimePerRound': [4500.0, 2400.0, 110000.0]}
Uwaga
Domyślnie środowisko uruchomieniowe jest wyświetlane w nanosekundach.
Tych danych można użyć do utworzenia pewnych wyjaśnień dotyczących sposobu produkcji wymaganych stanów T przez fabryki T.
data = result.data()
tfactory = data["tfactory"]
breakdown = data["physicalCounts"]["breakdown"]
producedTstates = breakdown["numTfactories"] * breakdown["numTfactoryRuns"] * tfactory["numTstates"]
print(f"""A single T factory produces {tfactory["logicalErrorRate"]:.2e} T states with an error rate of (required T state error rate is {breakdown["requiredLogicalTstateErrorRate"]:.2e}).""")
print(f"""{breakdown["numTfactories"]} copie(s) of a T factory are executed {breakdown["numTfactoryRuns"]} time(s) to produce {producedTstates} T states ({breakdown["numTstates"]} are required by the algorithm).""")
print(f"""A single T factory is composed of {tfactory["numRounds"]} rounds of distillation:""")
for round in range(tfactory["numRounds"]):
print(f"""- {tfactory["numUnitsPerRound"][round]} {tfactory["unitNamePerRound"][round]} unit(s)""")
A single T factory produces 1.68e-10 T states with an error rate of (required T state error rate is 2.77e-08).
23 copies of a T factory are executed 523 time(s) to produce 12029 T states (12017 are required by the algorithm).
A single T factory is composed of 3 rounds of distillation:
- 1368 15-to-1 space efficient physical unit(s)
- 20 15-to-1 RM prep physical unit(s)
- 1 15-to-1 RM prep logical unit(s)
Zmienianie schematu korekty błędów kwantowych
Teraz uruchom ponownie zadanie szacowania zasobów dla tego samego przykładu na podstawie parametrów kubitu opartego na majoranie ze schematem qecSchemeQEC floqued.
params = {
"qubitParams": {"name": "qubit_maj_ns_e6"},
"qecScheme": {"name": "floquet_code"}
}
result_maj_floquet = backend.run(circ, params).result()
EstimateDetails(result_maj_floquet)
Zmiana budżetu błędu
Uruchommy ponownie ten sam obwód kwantowy z wartością errorBudget 10%.
params = {
"errorBudget": 0.01,
"qubitParams": {"name": "qubit_maj_ns_e6"},
"qecScheme": {"name": "floquet_code"},
}
result_maj_floquet_e1 = backend.run(circ, params).result()
EstimateDetails(result_maj_floquet_e1)
Uwaga
Jeśli wystąpi jakikolwiek problem podczas pracy z narzędziem do szacowania zasobów, zapoznaj się ze stroną Rozwiązywanie problemów lub skontaktuj się z .AzureQuantumInfo@microsoft.com