Все существующие деревья
В прошлый раз мы говорили о том, что количество двоичных деревьев с количеством узлов, равным n равняется C(n), где C(n) – это n-ое число Каталана. В прошлом сообщении я задал вопрос о том, каких деревьев больше: произвольных или двоичных с заданным числом узлов n. Если вы нашли ответ на этот вопрос, то он мог вас удивить; он не является таким уж очевидным.
Первым распространённым ответом на этот вопрос был следующий: «Должно быть больше произвольных деревьев, поскольку двоичные деревья – это частный случай производных деревьев». Можете ли вы сказать, почему этот ответ неверный? Существует большее количество двоичных деревьев, чем произвольных! Есть два двоичных дерева из двух узлов: одно дерево с ненулевым левым потомком, а другое – с ненулевым правым потомком. Но существует только одно произвольное дерево с двумя вершинами, поскольку в этом случае нет разницы между «левым» и «правым» потомком.
Как оказалось, ответ на мой вопрос (кроме случаев с нулем узлов и одним узлом) заключается в том, что двоичных деревьев, состоящих из n узлов всегда больше, чем произвольных деревьев из n узлов.
Если вы действительно решите эту задачу, то заметили один интересный факт: количество произвольных деревьев, состоящих из n узлов равно С(n-1), т.е. существует 14 двоичных деревьев из 4 узлов и 14 произвольных деревьев из 5 узлов. Существует 1430 двоичных деревьев из 8 узлов и 1430 произвольных деревьев из 9 узлов. Странно! (Можно посмотреть на эту ситуацию с другой стороны: количество двоичных деревьев из n «пустых конечных узлов», равно количеству произвольных деревьев из n узлов)
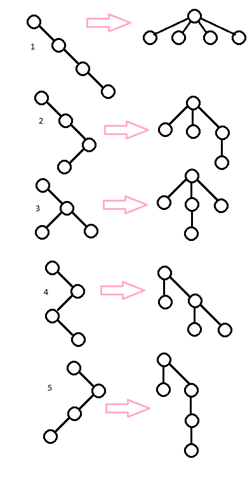
Очевидно, что это не может быть случайностью; должно быть однозначное соответствие между двоичными деревьями размера n и произвольными деревьями размера n+1. На самом деле, это соответствие легко увидеть, если посмотреть на задачу с правильной точки зрения (см. соответствующие рисунки). Слева я нарисовал соответствие первых 5 двоичных деревьев размера 4 (в том порядке, в котором я получу их с помощью моего кода из предыдущей статьи), а рядом – пять соответствующих произвольных деревьев размера 5 (вы можете кликнуть на изображение для получения более крупной версии).
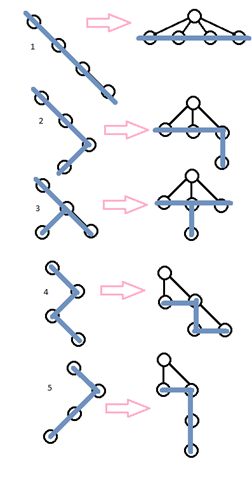
Чтобы сделать еще более понятным отношение между двумя типами деревьев, давайте рассмотрим диаграмму справа. Для преобразования двоичного дерева в соответствующее произвольное дерево, вам нужно повернуть его на 45 градусов против часовой стрелки, добавить сверху корень, а затем исправить все горизонтальные линии так, чтобы они указывали на соответствующих родителей.
Или, с точки зрения структур данных, можно представить каждый узел произвольного дерева, как указатель на первого ребёнка и указатель на следующего «брата». Это то же самое, что и двоичное дерево, только вместо подписей к вершинам «первый ребёнок» и «следующий брат» нужно написать «левый потомок» и «правый потомок». Единственным отличием между двоичным деревом и произвольным деревом в этой системе заключается в том, что правый потомок корня всегда пуст, поскольку корень не имеет братьев. Как только вы поймете, что разница между двоичным деревом и произвольным деревом заключается всего лишь в названиях полей структуры данных, строгая связь между ними станет очевидной.
Итак, решение второй части моего вопроса: уже готово. Поскольку у нас есть инструмент, который перечисляет все двоичные деревья, а у двоичных деревьев существует однозначное отношение с произвольными деревьями, тогда все, что нам нужно, это инструмент преобразования двоичных деревьев в произвольные. Решение этой задачи я оставляю в качестве домашнего задания, но ради интереса приведу алгоритм, который принимает двоичное дерево и возвращает строковое представление соответствующего произвольного дерева, с помощью краткого синтаксиса обозначения произвольного дерева, о котором я говорил в прошлой статье.
public static string TreeString(Node node)
{
// Получить строковое представление произвольного дерева, которое
// соответствует данному двоичному дереву
var sb = new StringBuilder();
Action<Node> f = null;
f = n =>
{
sb.Append("{");
for (Node child = n.Left; child != null; child = child.Right)
f(child);
sb.Append("}");
};
f(new Node(node, null));
return sb.ToString();
}
Для получения всех деревьев размером 5, мы запрашиваем все двоичные деревья размером 4 и выводим их, как произвольные деревья размером 5.
foreach (var n in AllBinaryTrees(4))
Console.WriteLine(TreeString(n));
и мы получим
{{}{}{}{}}
{{}{}{{}}}
{{}{{}}{}}
{{}{{}{}}}
{{}{{{}}}}
{{{}}{}{}}
{{{}}{{}}}
{{{}{}}{}}
{{{{}}}{}}
{{{}{}{}}}
{{{}{{}}}}
{{{{}}{}}}
{{{{}{}}}}
{{{{{}}}}}
Обратите внимание, что если вы уберёте внешние скобки, то получим решение задачи «вывести все корректные комбинации из четырёх пар скобок»! Если вы можете перечислить все двоичные деревья, тогда оказывается, что вы можете получить решения десятка других подобных задач.
В следующий раз: что еще мы можем сгенерировать?