Speaking of math…
This post discusses how a combination of the Office in-memory built-up format (“Professional” in Word) and UnicodeMath is ideal for generating speech for math zones. Neither format was designed with speech in mind. The built-up format was designed to aid the creation of beautiful math typography. UnicodeMath was designed to aid math keyboard input by looking as close as possible like real math. That goal is often achieved. For example, (a+b)/2 is, in fact, a valid mathematical expression. Fortuitously this goal also brings the notation closer to speech. One can understand the literal translation “open paren a plus b close paren over 2”.
Speech granularity
Understand at the outset that two granularities of math speech are needed: coarse-grained, which speaks math expressions fluently in a natural language, and fine-grained, which speaks the content at the insertion point. The coarse-grained granularity is great for scanning through math zones. It doesn’t pretend to be tightly synchronized with the characters in memory and cannot be used directly for editing. It’s relatively independent of the memory math model used in applications.
In contrast, the fine-grained granularity is tightly synchronized with the characters in memory and is ideal for editing. By its very nature, it depends on the built-up memory math model (described below), which is the same for all Microsoft math-aware products, but may differ from the models of other math products. Coarse grained navigation between siblings for a given math nesting level can be done with Ctrl+→ and Ctrl+← or Braille equivalents, while fine-grained navigation is done with → and ← or equivalents. The latter allows the user to traverse every character in the display math tree used for a math zone. The coarse- and fine-grained granularities are discussed further in the post Math Accessibility Trees. In addition to granularity, it’s useful to have levels of verbosity. Especially when new to a system, it’s helpful to have more verbiage describing an equation. But with greater familiarity, one can comprehend an equation more quickly with less verbiage.
Parentheses
To represent mathematics linearly and unambiguously, UnicodeMath may introduce parentheses that are removed in built-up form. Speaking the introduced parentheses can get confusing since it may be hard for the listener to track which parentheses go with which part of the expression. In the simple example above of (a+b)/2, it’s more meaningful to say “start numerator a plus b end numerator over 2” than to speak the parentheses. Or to be less verbose, leave out the “start”. This idea applies to expressions that include square roots, boxed formulas and other “envelopes” that use parentheses to define their arguments unambiguously. For the UnicodeMath square-root √(a^2-b^2), it’s clearer to say “square root of a squared minus b squared, end square root” instead of “square root of open paren a squared minus b squared close paren”. This is particularly true if the square root is nested inside a denominator as in
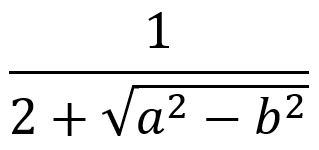 which has the UnicodeMath 1/(2+√(a^2-b^2)). By saying “end square root” instead of “close paren”, it’s immediately clear where the square root ends. Simple fractions like 2/3 are spoken using ordinals as in “two thirds”. Also when speaking the UnicodeMath text ∑_(n=0)^∞, rather than say “sum from open paren n equal 0 close paren to infinity”, one should say “sum from n equal 0 to infinity”, which is unambiguous without the parentheses since the “from” and “to” act as a pair of open and close delimiters. This and similar enhancements are discussed in the ClearSpeak specification and in Significance of Paralinguistic Cues in the Synthesis of Mathematical Equations. Such clearer start-of-unit, end-of-unit vocabulary mirrors what’s in memory. The parentheses introduced by UnicodeMath are not in memory since the memory version uses special delimiters as explained below. Parentheses inserted by the user are spoken as “open paren” and “close paren” provided they are the outermost parentheses. Nested parentheses are spoken together with their parenthesis nesting level as in “open second paren”, “open third paren”, etc.
which has the UnicodeMath 1/(2+√(a^2-b^2)). By saying “end square root” instead of “close paren”, it’s immediately clear where the square root ends. Simple fractions like 2/3 are spoken using ordinals as in “two thirds”. Also when speaking the UnicodeMath text ∑_(n=0)^∞, rather than say “sum from open paren n equal 0 close paren to infinity”, one should say “sum from n equal 0 to infinity”, which is unambiguous without the parentheses since the “from” and “to” act as a pair of open and close delimiters. This and similar enhancements are discussed in the ClearSpeak specification and in Significance of Paralinguistic Cues in the Synthesis of Mathematical Equations. Such clearer start-of-unit, end-of-unit vocabulary mirrors what’s in memory. The parentheses introduced by UnicodeMath are not in memory since the memory version uses special delimiters as explained below. Parentheses inserted by the user are spoken as “open paren” and “close paren” provided they are the outermost parentheses. Nested parentheses are spoken together with their parenthesis nesting level as in “open second paren”, “open third paren”, etc.
Built-up format
Such refinements can be made by processing the UnicodeMath, but some parsing is needed. It’s easier to examine the built-up version of expressions, since that version is already largely parsed. The built-up format is a display tree as described in the post Math Accessibility Trees. For example, to know that an exponent in the UnicodeMath equation a^2+b^2=c^2 is, in fact, a 2 and not part of a larger argument, one must check the character following the 2 to make sure that it’s an operator and not part of the exponent. If the letter z follows the 2 as in a^2z, the z is part of the superscript and the expression should be spoken as “a to the power 2z”. In memory one just checks for a single code, here the end-of-object code U+FDEF. If that code follows the 2, the exponent is 2 alone and “squared” is appropriate, unless exponents are indices as in tensor notation.
The built-up memory format represents mathematical objects like fraction, matrix and superscript by a start delimiter, the first argument, an argument separator if the object has more than one argument, the second argument, etc., with the final argument terminated by the object end delimiter. For example, the UnicodeMath fraction a/2 is represented in the built-up format by {frac a|2} where {frac is the start delimiter, | is the argument separator, and } is the end delimiter. Similarly a^2 is represented in the built-up format by {sup a|2 }. Here the start delimiter is the same character for all math objects and is the Unicode character U+FDD0 in RichEdit (Word uses a different character). The type of math object is given by a rich-text object-type property associated with the start delimiter as described in ITextRange2::GetInlineObject(). The RichEdit argument separator is U+FDEE and the object end delimiter is U+FDEF. These Unicode codes are in the U+FDD0..U+FDEF “noncharacters” block reserved for internal use only.
Fine-grained navigation
Another scenario where the built-up format is very useful for speech is in traversing a math zone character by character, allowing editing along the way. Consider the integral
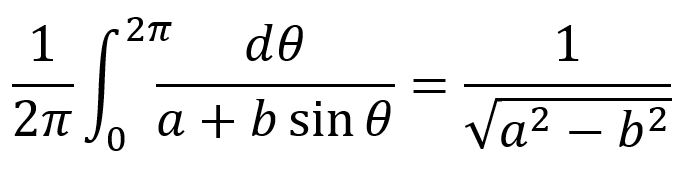 When the insertion point is at the start of the math zone, “math zone” is spoken followed by the speech for the entire math zone. But at any time the user can enter → (or Braille equivalent), which halts the math-zone speech, enters the numerator of the leading fraction, and speaks “1”. Another → and “end of numerator” is spoken. Another → and “2 pi” is spoken. Another → and “end of denominator” is spoken and so forth. In this way, the user knows exactly where the insertion point is and can edit using the usual input methods.
When the insertion point is at the start of the math zone, “math zone” is spoken followed by the speech for the entire math zone. But at any time the user can enter → (or Braille equivalent), which halts the math-zone speech, enters the numerator of the leading fraction, and speaks “1”. Another → and “end of numerator” is spoken. Another → and “2 pi” is spoken. Another → and “end of denominator” is spoken and so forth. In this way, the user knows exactly where the insertion point is and can edit using the usual input methods.
This approach is quite general. Consider matrices. At the start of a matrix, “n × m matrix” is spoken, where n is the number of rows and m is the number of columns. Using →, the user moves into the matrix with one character spoken for each → up until the end of the first element. At that end, “end of element 1 1” is spoken, etc. Up and down arrows can be used to move vertically inside a matrix as elsewhere, in all cases with the target character or end of element being spoken so that the user knows which element the insertion point is in.
Variables and ordinary text
Math variables are represented by math alphabetics (see Section 2.2 of Unicode Technical Report #25). This allows variables to be distinguished easily from ordinary text. When converted to speech text, such variables are surrounded by spaces when inserted into the speech text. This causes text-to-speech engines to say the individual letters instead of speaking a span of consecutive letters as a word. In contrast, an equation like rate = distance/time, would be spoken as “rate equals distance over time”. Math italic letters are spoken simply as the corresponding ASCII or Greek letters since in math zones math italic is enabled by default. Other math alphabets need extra words to reveal their differences. For example, ℋ is spoken as “script cap h”. Alternatively, the “cap” can be implied by raising the voice pitch.
Some special cues may be needed to convince text-to-speech engines to say math characters correctly. For example, ‘+’ may need to be given as “plus”, since otherwise it might be spoken as “and”. The letter ‘a’ may need to be enclosed in single quotes, since otherwise it may be spoken as the ‘a’ in “zebra” instead of the ‘a’ in “base”.
Tweaks
Another example of how the two speech granularities differ is in how math text tweaking is revealed. First, let’s define some ways to tweak math text. You can insert extra spaces as described in Sec. 3.15 of the UnicodeMath paper. Coarse-grained speech doesn’t mention such space but fine-grained speech does. More special kinds of tweaking are done by inserting phantom objects. Five Boolean flags characterize a phantom object: 1) zero ascent, 2) zero descent, 3) zero width, 4) show, and 5) transparent. Phantom objects insert or remove precise amounts of space. You can read about them in the post on MathML and Ecma Math (OMML) and in Sec. 3.17 of the UnicodeMath paper. The π in the upper limit of the integral above is inside an “h smash” phantom, which sets the π’s width to 0 (smashes the horizontal dimension). Notice how the integrand starts at the start of the π. Coarse-grained speech doesn’t mention this and other phantom objects and only includes their contents if the “show" flag is set. Fine-grained speech includes the start and end entities as well as the contents. This allows a user to edit phantom objects just like the 22 other math objects in the LineServices math model.
The approaches described here produce automated math speech; the content creator doesn’t need to do anything to enable math speech. But it’s desirable to have override capability, since the heuristics used may not apply or the content author may prefer an alternate phrasing.
Comments
- Anonymous
June 30, 2016
great resources