Une illustration du Deep Learning : Monitorer son activité quotidienne en temps réel – 1ère partie
Introduction
Dans le cadre de ce billet, et pour faire suite au précédent billet Une première introduction au Deep Learning, nous vous proposons, Morgan Funtowicz actuellement en stage au sein de l'équipe et moi-même, de poursuivre notre exploration des concepts relatifs aux algorithmes de Deep Learning. L'idée consiste ici à pouvoir appréhender d'une façon générale un certain nombre de concepts liés aux réseaux de neurones et à commencer à manipuler les différentes briques permettant de mettre en place de tels algorithmes.
Pour illustrer ce billet, nous invitons à mettre en place un système capable de détecter en temps réel un ensemble d'activités humaines prédéfinies.
Dans la pratique, un tel dispositif pourrait s'apparenter à un bracelet connecté, tel que le Microsoft Band, permettant de rendre compte de l'activité journalière d'un individu.
Cependant, à la différence du bracelet, l'idée consiste à s'appuyer uniquement sur les données issues de l'accéléromètre inclus aujourd'hui dans tous les smartphones modernes.
Ce billet s'inscrit dans la continuité du billet précédent. Il suppose donc une compréhension des concepts de base du fonctionnement des réseaux de neurones.
Description des données
Afin de mettre en place notre solution, et de façon à en simplifier la mise en œuvre concrète, nous allons utiliser directement un jeu de données mis à disposition par l'UCI (disponible ici), contenant les valeurs émises par l'accéléromètre d'une dizaine de personnes filmée en continu (dans le but de labéliser le plus fidèlement ces données).
Les activités à identifier dans le jeu de données sont les suivantes :
- Assis devant un ordinateur
- En train de se lever
- Debout
- En train de marcher
- En train de monter / descendre des escaliers
- En train de marcher et de parler
- Debout en train de parler
Si vous n'êtes pas familier d'un accéléromètre, il s'agit d'un capteur présent dans de nombreux systèmes actuels, comme notamment les smartphones comme nous les sous-entendions ci-avant, permettant de détecter l'accélération d'un objet dans l'espace. Cette accélération est représentée selon 3 axes (X, Y, Z) chacun des axes caractérisant un certain type de mouvement.

Figure 1 : Représentation schématique d'un accéléromètre
Les données sont émises par le capteur à intervalles réguliers, (dans notre cas, 52 fois par seconde, soit 52Hz). Nous nous retrouvons donc dans le monde de l'analyse des séries temporelles (time-series).
L'analyse de ce genre de données est devenue monnaie courante avec les objets connectés et l'Internet des objets.

Figure 2 : Exemple de série temporelle générée par les 3 dimensions de l'accéléromètre
Transformation des données
Fort de ces données, voyons comment les traiter.
Une première approche
Une première approche consisterait à essayer de fournir les données brutes à l'algorithme, sans aucun prétraitement. Une telle approche fait l'hypothèse que les mesures à l'instant T et celle à l'instant T+1 sont indépendantes l'un de l'autre.
Cependant, cette hypothèse n'est pas réaliste dans les faits. En effet, pour passer d'un état S1 à un état S2, nous accusons tous une phase de transition. Cette notion temporelle est aussi valable pour des mouvements complexes, tels que la marche, la course à pieds, etc. En effet, pour caractériser ces actions, il s'agit en fait de pouvoir identifier des motifs récurrents caractérisant une action dans le temps.
Une approche par fenêtrage
Afin de pouvoir capter ces variations et ces motifs, nous introduisons la notion de fenêtre d'observation. Ainsi, au lieu d'observer indépendamment chacun des relevés, nous allons estimer une tendance au sein de cette fenêtre de temps.
La tendance permet à l'algorithme de caractériser les variations : « une augmentation conséquente sur l'axe des X, une stagnation sur l'axe des Y ».
De plus, le fenêtrage permet de générer des motifs beaucoup complexes que ceux que l'on pourrait déterminer sur une seule observation.
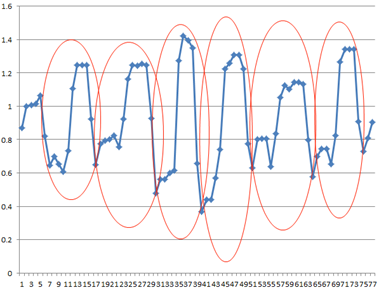
Figure 3 : Exemple de motifs dans les séries temporelles
Cependant, avec une approche de ce type, la modélisation des variations se révèle assez complexe, notamment au niveau de la granularité souhaitée sur les variations (tendance globale, par portion, etc.)
Approche dans le domaine fréquentiel
Afin de résoudre ce problème, nous allons utiliser une méthode très employée dans le domaine du traitement du signal, qui est le passage dans le domaine fréquentiel.
Bravo aux plus téméraires d'entre vous qui n'ont pas quitté ce billet en lisant ces dernières lignes ;)
La fréquence se définit comme le nombre d'apparition d'un phénomène par unité de temps : 2 fois par secondes, 1 fois par an, toutes les minutes, etc.
Une des transformations usuelles pour passer d'un domaine temporel (comme c'est le cas pour nos données) à un domaine fréquentiel est la Transformée de Fourier
(Nous ne détaillerons pas forcément dans le détail le fonctionnement de cette opération mathématique, car elle dépasse de loin le cadre de ce billet).
Vous avez surement déjà eu à faire à cette transformation sans le savoir. Elle est notamment utilisée sur les appareils musicaux pour modéliser le spectre d'un son :

Figure 4 : Exemple d'un extrait de chanson dans le domaine fréquentiel
Pour les moins audiophiles d'entre nous, voici comment interpréter ce graphique :
- La partie gauche du graphique représente les basses fréquences, plus couramment appelées les basses.
- La partie droite représente les hautes fréquences, à savoir les aigües.
- Les différentes valeurs prisent par le signal dans le domaine temporel (potentiellement un nombre infini de valeurs possibles) sont discrétisées : on parle alors de catégories, groupes, paquets, etc.
- Enfin la hauteur de chaque « barre » représente le nombre d'occurrence des valeurs appartenant à chaque catégorie (un histogramme).
Grace à cet outil, nous pouvons désormais aisément caractériser un motif, non pas par son allure, mais par la manière dont il est composé : plus de valeurs basses que de valeurs hautes par exemple.
Combinaison des deux méthodes précédentes
Maintenant que nous avons passé en revue les différentes approches possibles, vous êtes en droit de vous demander quelle modélisation est la plus adaptée. La réponse est, une combinaison des deux méthodes.
Pour ce faire, nous allons utiliser un dernier outil, lui aussi issu du domaine de l'analyse des signaux : Le spectrogramme.

Figure 5 : Spectrogramme d'un signal
Ce graphique, qui pourrait se rapporter à de l'art abstrait ;) constitue en fait la manière de représenter les variations dans le domaine fréquentiel :
- Sur l'axe horizontal nous représentons le temps
- Sur l'axe vertical les fréquences
- Et enfin, la couleur nous apporte l'information sur la puissance.
Il s'agit, plus concrètement, de représenter des Transformées de Fourier consécutives en fonction du temps.
Ainsi, nous pouvons identifier les variations des motifs du signal en fonction du temps. C'est d'ailleurs cette représentation que nous utiliserons pour modéliser notre problème.
Topologie de notre réseau de neurones
Avant d'entrée dans l'apprentissage effectif de notre solution de Deep Learning, il convient de réfléchir à quelques points importants qui constitueront notre réseau de neurones, en l'occurrence :
- La taille de la fenêtre de temps à utiliser,
- Le nombre de variables en entrée,
- Le nombre de classe à prédire,
- Le nombre de couches cachées,
- Le nombre de neurones par couche,
- Les fonctions d'activations à utiliser,
- Les transformations éventuelles qu'opèrera notre solution de Deep Learning, Cf. billet précédent.
Revenons sur la Transformée de Fourier. Cette dernière possède une propriété intéressante, qui est la suivante : Pour une fonction dont les valeurs sont réelles (notre cas), la partie positive du spectre est le conjugué de la partie négative. Etant donné la relation entre ces deux parties, nous pouvons nous passer de l'une d'entre elles, car redondante. Plus concrètement, il s'agit de supprimer la moitié du spectre généré.
Ce qui nous donne donc (pour une fenêtre de 10 secondes) :
- 52 évènements par secondes, sur 10 secondes = 520 évènements
- 3 axes (X, Y, Z)
Après passage dans la Transformée de Fourier :

Cependant, à ce nombre de dimensions, nous pouvons encore retirer la fréquence 0, car cette dernière n'est que la somme de toutes les autres. Nous obtenons ainsi 777 – 3 = 774. (Nous retirons la fréquence 0 trois fois car cette dernière est dans le spectrogramme de chacun des axes).
Les entrées et sortie de notre réseau seront donc configurées de la manière suivante :
- Le nombre de variables en entrée : 774
- Le nombre de classe à prédire : 7
Les valeurs répercutées ici, notamment la taille de la fenêtre, sont issues des résultats fournit par cet article de recherche et avons choisi de représenter notre réseau de neurones avec 3 couches cachées de 300 neurones.
Ceci clôt ainsi la première partie de ce billet. La seconde partie s'intéresse à la mise en œuvre à proprement parlé de la solution. Nous nous appuierons pour cela sur le projet CNTK (Computational Network ToolKit) développé par Microsoft Research et disponible sur le repo/la forge communautaire GitHub.