Un peu de théorie pour l'apprentissage non-supervisé
De façon à rentrer de plein pied dans le monde du Machine Learning, nous souhaitons partager une compréhension commune des principes de l’apprentissage automatique, et expliquer au travers d’une série courte de billet ce qu’est l’apprentissage supervisé et non-supervisé avec des applications ainsi que les moyens d’évaluer un modèle en apprentissage automatique.
Ce billet est pour l’essentiel une republication sur ce blog du billet éponyme déjà publié sur le blog MSDN Big Data France .
Je vous souhaite une bonne lecture de ce billet
--Philippe
_________________________________________________________________________________________
Nous avons appliqué des méthodes d’apprentissage non supervisé pour analyser des logs de proxy dans le billet précédent.
Dans le cadre de ce billet, nous vous proposons à titre de complément de voir dans les détails comment fonctionnent ces algorithmes et les possibilités qu’ils offrent.
L’apprentissage non-supervisé consiste à tirer de la valeur de données dans lesquelles l’attribut à prédire n’apparaît pas. Dans notre exemple précédent d’analyse de logs, les méthodes d’apprentissage non-supervisé nous ont servi à détecter les éléments anormaux dans les données, sans pour autant que cette information apparaisse de manière explicite.
On distingue 3 principales tâches réalisables à partir de méthodes d’apprentissage non-supervisé :
- Le partitionnement des données (clustering).
- La détection d’éléments atypiques (outlier detection).
- La réduction de dimensions.
Nous allons détailler de manière très succincte le fonctionnement de certains des algorithmes permettant d’effectuer ces tâches.
Partitionnement des données – Clustering
Le clustering consiste à regrouper les données en groupes homogènes appelés classes ou clusters, de sorte que les éléments à l’intérieur d’une même classe soient similaires, et les éléments appartenant à deux classes différentes soient différents. Il faut donc définir une mesure de similarité entre deux éléments des données : la distance.
Choix d’une distance
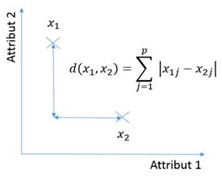
Chaque élément peut être défini par les valeurs de ses attributs, ou d’un point de vue mathématique par un vecteur ou un point. Le nombre d’éléments de ce vecteur est le même pour tous les éléments et est appelé la dimension du vecteur, notée n ici. Etant donnés deux vecteurs x1 et x2, il faut définir la distance entre ces deux éléments d(x1, x2).
Parmi les choix les plus classiques, on retrouve :
- La distance euclidienne. C’est la distance à vol d’oiseau entre 2 points. Etant donné deux points A et B repérés par leurs coordonnées X et Y, on a :
- La distance de Manhattan. Le nom de cette distance est inspirée du fameux quartier de New York, constitué de nombreux gratte-ciels. Il est impossible de se rendre d’un point à un autre à vol d’oiseau, il faut contourner les bâtiments :
- La distance de Hamming. Cette distance mesure la similitude entre 2 mots en comptant le nombre de caractères qui diffèrent. Par exemple, la distance de Hamming entre ‘manche’ et ‘mouche’ est égale à 2.
Principe des algorithmes de clustering
Les algorithmes de clustering consistent à assigner des classes en respectant les règles suivantes :
- La distance entre les éléments d’une même classe (distance intra-classe) est minimale.
- La distance entre chaque classe (distance inter-classes) est maximale.

Toutefois, pour résoudre de manière exacte ce problème, il faudrait essayer toutes les combinaisons possibles d’assignations des éléments à des classes, et choisir la solution ayant les distances intra-classe minimales, et les distances inter-classes maximales.
Pour assigner des classes à 27 éléments de manière optimale, il faudrait 115094595070 années à un processeur de 3 GHz pour réaliser cette tâche, soit environ 100 fois l’âge de l’univers…
C’est pour cela que l’on utilise différents algorithmes appelés approximations ou heuristiques afin de trouver la solution la plus proche possible de la solution optimale en un temps raisonnable. Nous allons détailler quelques-uns de ces algorithmes.
Clustering basé sur la représentation : illustration avec k-moyennes (k-means)
Les algorithmes basés sur la représentation consistent à désigner un représentant pour chaque classe afin de calculer les distances plutôt que calculer des distances avec tous les éléments d’une même classe. Dans k-means, le représentant d’une classe est souvent le barycentre des points de cette classe (généralisation de la moyenne).
Le fonctionnement de l’algorithme est le suivant :
- Initialisation : le nombre de classes K étant imposé, choisir K points aléatoirement pour constituer initialement les représentants de chaque classe
- Pour chaque point :
- Calculer les distances entre ce point et les représentants des classes
- Affecter à ce point la classe avec laquelle sa distance est minimale
- Mettre à jour les représentants de chaque classe (par exemple, calcul de barycentre)
Il existe de nombreuses variantes de cet algorithme (K-médoïdes (k-medoids), K-medians).
Clustering hiérarchique
L’algorithme k-means a l’avantage d’être une méthode extrêmement simple à appliquer, mais elle est peu robuste car elle est très sensible aux outliers. Ainsi, ajouter un élément atypique peut complètement modifier le partitionnement des données.
Une alternative est le clustering hiérarchique. On distingue le clustering hiérarchique agglomératif et le clustering hiérarchique de division.
Le fonctionnement du clustering hiérarchique agglomératif est le suivant :
- Initialisation : chaque point est une classe
- Tant qu’il reste des points à classer :
- Calculer toutes les distances entre les points à classer et les représentants des classes
- Fusionner les 2 classes les plus proches
- Fusionner les classes les plus proches jusqu’à obtenir le nombre de classes voulu
On visualise souvent l’application d’un algorithme de clustering hiérarchique sous la forme suivante :
Le partitionnement final s’effectue en fusionnant progressivement les feuilles de l’arbre représenté ci-dessus.
Clustering basé sur la densité
Plutôt que de considérer les distances entre les éléments, on peut introduire la notion de densité. Si un élément a de nombreux voisins, il aura une forte densité. Inversement, si tous ses voisins sont éloignés, sa densité sera faible (et par conséquent il sera considéré comme du bruit). Ces méthodes de clustering permettent de s’affranchir du choix du nombre de classes et permettent d’éliminer les éléments aberrants.
Comment définir formellement la notion densité ?
La densité D d’un point P est définie par le nombre d’éléments à une distance de P inférieure à![clip_image002[4] clip_image002[4]](https://msdntnarchive.z22.web.core.windows.net/media/MSDNBlogsFS/prod.evol.blogs.msdn.com/CommunityServer.Blogs.Components.WeblogFiles/00/00/01/57/01/metablogapi/5023.clip_image0024_thumb_4B079E18.png) .
.
inférieure à .
Pour parler de densité, il faut donc fixer le paramètre , ce qui peut être assez empirique.
Un des algorithmes utilisant la densité est DBSCAN :
- Pour chaque point non visité :
- Calculer sa densité
- Si cette densité est plus petite qu’un seuil à préciser, le point est considéré comme bruit, donc associé à aucun cluster
- Sinon, affecter ce point et tout son voisinage à la même classe
En particulier, on remarque que DBSCAN procède à une détection d’outliers ;)
Et aussi…
Il existe de nombreuses autres méthodes de clustering. Certaines font partie de la catégorie ‘soft clustering’, c’est-à-dire, plutôt d’affecter une classe à chaque élément, ces méthodes calculent les probabilités d’appartenance à chaque classe (Fuzzy k-means par exemple). Certaines sont à privilégier si on a des aprioris sur la répartition des données (EM, mélange de Gaussiennes…).
Détection d’éléments atypiques
Les éléments atypiques ou outliers sont ceux qui ont peu d’éléments dans leur voisinage.
Elle peut être effectuée par des algorithmes basés sur la notion de densité comme DBSCAN ou LOF. LOF est très similaire à DBSCAN donc nous ne la détaillons pas ici.
La réduction de dimensions
Lorsque chaque élément est défini par un grand nombre d’attributs, il est difficile de travailler sur les données de manière intuitive. L’idée est de réduire le nombre d’attributs qui décrivent les données, idéalement 2, afin de pouvoir visualiser les données sur un écran.
Analyse en composantes principales (ACP)
A partir de tous les attributs de base, on souhaite déterminer un certain nombre de nouveaux attributs qui conservent la distance entre les éléments. Ces attributs sont exprimés en tant que combinaisons linéaires des attributs de base dans l’ACP. On appelle alors les nouveaux attributs composantes principales.
Sans détailler la théorie mathématique de l’ACP, il faut retenir que :
- Les composantes principales sont calculées de manière incrémentale, donc il est aisé de calculer peu de composantes (en particulier visualiser les données dans un espace à 2 dimensions)
- Plus on garde de composantes, plus la représentation des données est complète. En particulier, il peut être intéressant d’effectuer systématiquement une analyse en composantes principales en gardant le même nombre de composantes afin de trouver une meilleure représentation des données, notamment avant d’appliquer un algorithme d’apprentissage non-supervisé.
Autres…
Il existe des méthodes supervisées de réduction de dimensions qui tirent parti de la corrélation entre les attributs et le résultat comme la régression PLS. Elles sont à privilégier par rapport à l’ACP lorsque les données sont labélisées.
Nous en avons terminé de l’éclairage complémentaire que nous souhaitions donner au billet précédent.