An almost exact decimal
Recently I was working with a very interesting case, involving Automation, and AL runtime. This involves the number of decimals that NAV supports; giving the sensation that rounding is done incorrectly.
First, I would like to bring you your attention to Table 370 (Excel Buffer). This table provides a very simple way to read and write Excel files. This works pretty neatly, except when you start dealing with some “special numbers”.
The issue, really, is that decimals, when transported via COM, are encoded in a VT_R8, which means that we have 64 bits to express all decimal values (according to MSDN, VT_R8 is an IEEE 8-byte), which basically means, they cannot express extremely precise values.
Now, how exactly precisely is precise? Let’s work with 17.7.
Well, don’t think that NAV, or for that matter COM, cannot express this “simple” value, the problem is really they way decimals are encoded.
Let me first show you the issue, as it is pretty simple to reproduce.
First, create an Excel file using Microsoft Excel. On cell A1 of a Sheet, type “17.7”. Now, this by itself is tricky, because what you need to type depends on your Locale. What I mean is seventeen and 7/10 (meaning, that you might have to use comma instead of a dot).
Save the recently created file someplace that you can remember.
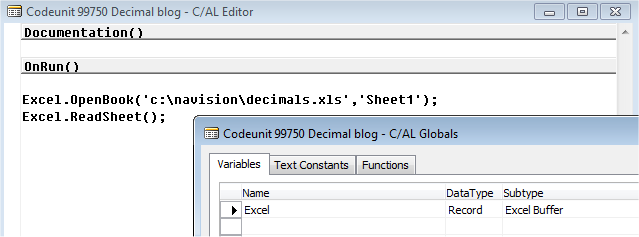
Now create a codeunit, with one global variable of type record of Subtype “Excel Buffer”.
Then open your file and refer to your Sheet, and read it, just like this:
It is time to see the inserted value, for that, go to Table 370. You will see that the Cell value is in fact “17.699999999999999” (if you see 17.7 is because your NAV version is not as accurate as the one I am using, or the codeunit has already been modified for rounding).
You must be thinking now that I am trying to sell you a platform bug as a feature, but this not the case. The problem, really, is that recent NAV builds recognizes more decimals (up to 18), and an 8 byte IEEE is not as precise. To illustrate this, look at the following table:
Decimal Floating-Point: |
64 bit Hexadecimal (memory representation): |
17.699999999999995 |
4031B33333333332 |
17.699999999999996 |
4031B33333333332 |
17.699999999999997 |
4031B33333333332 |
17.699999999999998 |
4031B33333333333 |
17.699999999999999 |
4031B33333333333 |
17.700000000000000 |
4031B33333333333 |
17.700000000000001 |
4031B33333333333 |
17.700000000000002 |
4031B33333333334 |
17.700000000000003 |
4031B33333333334 |
17.700000000000004 |
4031B33333333335 |
In here, it is clear that the hexadecimal representation “4031B33333333333”, not only refers to 17.7, but also to some “neighboring” values (actually 4 values), so, the COM algorithms seem to choose the most likely one: the middle, which in fact, is really a close approximation.
The reason why decimal accuracy was increased in NAV was precisely to improve calculations when dealing either with very large numbers, or very accurate ones, the consequence being that 64 bit representation cannot deal with so many decimals.
Fortunately, in order to prevent this from happening, you can round the values to be less precise, which in most cases will give you the values that you were in fact expecting, so for decimals, you could round to 4 decimals using variants (in order to know if you are dealing with a decimal number or not):
"Cell Value" := XlWrkSht.Range(xlColID + xlRowID).Value;
IF ("Cell Value".ISDECIMAL) THEN
BEGIN
"Cell Decimal Value" := "Cell Value";
"Cell Decimal Value" := ROUND("Cell Decimal Value", 0.0001);
"Cell Value as Text" := FORMAT("Cell Decimal Value");
END
ELSE
"Cell Value as Text" := DELCHR(FORMAT(XlWrkSht.Range(xlColID + xlRowID).Value),'<',' ');
Hopefully this will clarify why you can get this approximations, and how to deal with it in C/AL.
Jorge Alberto Torres
Software Developer Engineer
These postings are provided "AS IS" with no warranties and confer no rights. You assume all risk for your use.