Awesome F# - Decision Trees – Part I
Programming F# is out! Meaning you can, and should, go to the store and pick up a copy today.
With Programming F# serving as a solid guide for the F# Language, I’d like to start posting less about language features and more about applications. That is, what can you do with this awesome language.
This is the first blog post in a series titled Awesome F# . These posts will provide advanced, real-world applications of the F# language to do awesome things. This post is about Decision Trees and the ID3 algorithm, motivated by this question on StackOverflow.com.
If you want to learn more about data mining and machine learning THE BOOK you need to get is Machine Learning by Tom Mitchell. I’ll give a warning however, it is the most academically rigorous and dense book I’ve ever read. Seriously, not for the faint of heart!
Defining the Problem
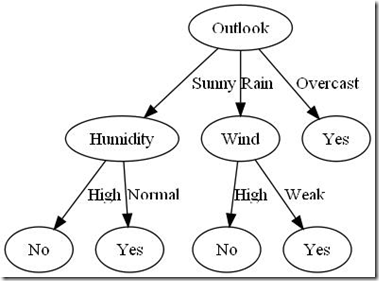
So what does the ID3 algorithm do? It is a technique for creating decision trees much like the following used for determining whether or not to play tennis. Starting at the topmost node, if the outlook is overcast then you should play tennis. If it is rainy however, you should play tennis only if the wind is weak.
In addition to helping plan your sports activities, decision trees are an easy way to gather business intelligence. Imagine you run mid-sized paper company in Scranton, Pennsylvania. You have a database filled with IP addresses of people who have visited your site, special deals you’ve offered them on your products, and whether or not they ended up purchasing some paper.
This is a situation where you want to apply data mining to extract meaning from the data. In this case, how to optimize your sales.
There are many different data mining algorithms based on the type of data you have and what you are looking for. In this blog post I will be covering decision trees, which is a machine learning technique for predicting a concept based on data. (For example, given a browser session predict if the user will purchase something.)
More formally: given a set of instances represented as name/value pairs - where the values are discrete - create a decision tree to most accurately classify any new instances. In the example above the name value pairs were Outlook : {Sunny, Rainy, Overcast} and the classification was ‘should you plan tennis’.
The Approach
The simplest way to do this is to generate tree branches greedily. Given your training data, find the best branch first and then moving on with more specific subsets of rules on reduced data sets. For example, if trying to determine if someone will purchase a product from your website whether or not they are a returning customer is probably the most significant piece of information.
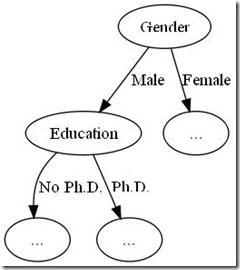
To find the ‘best split’ we will use an approach known as information again . But first, let’s look at a concept from information theory called entropy. Imagine you want to create a decision tree to determine if someone is an evil genius. Each datum may contain information such as gender and whether or not they had a Ph.D.
Entropy and information gain are metrics for calculating how much you learned from taking a given branch. If exactly 50% of evil geniuses are men, then you have learned nothing by branching on gender. (Since the same number of evil geniuses will be on the left side of the tree as the right side of the tree.) However, for determining evil geniuses education is likely very important – since we can assume the majority of evil geniuses have a Ph.D. in malevolence. In that case the decision tree branch is very effective at whittling down the data into a homogenous group: evil genius or not.
Enter the Mathematics
While information gain and entropy are simple concepts, the math is a bit intimidating. Let’s carry on with the ‘is an evil genius’ predictor using the following data:
| Gender | Education | Is Evil Genius? |
| Female | No Ph.D. | No |
| Male | No Ph.D. | No |
| Male | No Ph.D. | No |
| Female | No Ph.D. | No |
| Female | No Ph.D. | No |
| Male | No Ph.D. | No |
| Male | No Ph.D. | No |
| Female | No Ph.D. | No |
| Female | No Ph.D. | No |
| Male | No Ph.D. | Yes |
| Male | No Ph.D. | Yes |
| Female | No Ph.D. | No |
| Female | No Ph.D. | No |
| Male | No Ph.D. | No |
| Male | No Ph.D. | No |
| Female | No Ph.D. | No |
| Female | No Ph.D. | No |
| Male | No Ph.D. | No |
| Male | No Ph.D. | No |
| Female | No Ph.D. | No |
| Female | No Ph.D. | No |
| Male | No Ph.D. | No |
| Male | No Ph.D. | No |
| Female | No Ph.D. | No |
| Female | No Ph.D. | No |
| Male | Ph.D. | Yes |
| Male | Ph.D. | Yes |
| Female | Ph.D. | Yes |
| Female | Ph.D. | Yes |
| Male | Ph.D. | No |
Entropy
Given a set of data, S, which can be divided c ways with the probability of each division being p the entropy of that set is given by:
For example, if out of a set of six evil geniuses only four are men what is the entropy of that set?
Or 0.9182. Now, if out of that set of five people with Ph.D.s, four were evil geniuses. What is the entropy there?
Or 0.6883. That lower number means that it requires less information to encode that the evil geniuses of the log have a Ph.D. If you run the math for entropy, it will be zero when everything in a set has the same type and exactly 1 when its a 50/50 split. Looking something like this:
(Image generated from Wolfram Alpha.)
So the entropy for a homogenous set is lower than that of a mixed set. This is important because in our decision tree we want to narrow the data into more specific values – so we can make predictions more accurately.
Information Gain
Now that we know how to measure how homogenous a set of data is, how do we go about deciding the best attribute to branch on? That is, do we branch on gender, has a Ph.D., or some other attribute? To calculate this we can use the information gain function defined as:
Given a set of values, S, and an attribute of each datum in that set, A, determine how much information has been gained by branching on that attribute. Note that Sv is the subset of values S where each element has attribute value v.
So what is the information gained by putting our root branch at ‘has a Ph.D'.’ or not?
Or 0.2002. If we calculated the information gain from branching on gender, the result is –0.0513. So the math backs up our assertion that Ph.D. is a more significant factor in determining evil genius than gender. (Which makes sense since 4/5ths of the Ph.D.s are evil, whereas only 2/25ths of the non Ph.D.s are evil.)
Putting it Together
In Part II we’ll implement the ID3 algorithm in F#, which generally goes through the following process:
- Find the attribute that leads to the most information gain.
- Add a branch for that attribute.
- For each child node, repeat until all the data have the same classification.
Comments
Anonymous
November 01, 2009
The comment has been removedAnonymous
November 01, 2009
Yes, machine learning definitely falls into the "it's easier to do in F# than C#" camp due to the mathematical nature. I'm happy to hear you're putting F# to good use.Anonymous
November 01, 2009
Please more like this (i.e., applications or how to use F# in to solve problems)Anonymous
November 02, 2009
The comment has been removedAnonymous
November 03, 2009
Re: multiple regression analysis, if there is a clear trend in the data you can likely arrive at it through multiple means. (In the Evil Genius example, having a Ph.D. is the only significant bit.) However, decision trees offer a few advantages. For example, there are some algorithms which work 'online' meaning that they build up the decision tree as training data comes in. (Meaning it gets more accurate over time and doesn't need 'learning time'.) There are many things not covered by this blog post such as overfitting your training data or boosting to improve your trees accuracy. If you want to learn more about techniques for machine learning Tom Mitchell's book is really, really good.
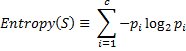
![clip_image002[16] clip_image002[16]](https://msdntnarchive.z22.web.core.windows.net/media/TNBlogsFS/BlogFileStorage/blogs_msdn/chrsmith/WindowsLiveWriter/AwesomeFDecisionTreesPartI_131F5/clip_image002%5B16%5D_thumb.gif)
![clip_image002[18] clip_image002[18]](https://msdntnarchive.z22.web.core.windows.net/media/TNBlogsFS/BlogFileStorage/blogs_msdn/chrsmith/WindowsLiveWriter/AwesomeFDecisionTreesPartI_131F5/clip_image002%5B18%5D_thumb.gif)
![clip_image002[12] clip_image002[12]](https://msdntnarchive.z22.web.core.windows.net/media/TNBlogsFS/BlogFileStorage/blogs_msdn/chrsmith/WindowsLiveWriter/AwesomeFDecisionTreesPartI_131F5/clip_image002%5B12%5D_thumb.gif)
![clip_image002[1] clip_image002[1]](https://msdntnarchive.z22.web.core.windows.net/media/TNBlogsFS/BlogFileStorage/blogs_msdn/chrsmith/WindowsLiveWriter/AwesomeFDecisionTreesPartI_131F5/clip_image002%5B1%5D_thumb.gif)
![clip_image002[3] clip_image002[3]](https://msdntnarchive.z22.web.core.windows.net/media/TNBlogsFS/BlogFileStorage/blogs_msdn/chrsmith/WindowsLiveWriter/AwesomeFDecisionTreesPartI_131F5/clip_image002%5B3%5D_thumb.gif)