Metrische codegegevens - Cyclomatische complexiteit

Wanneer u met metrische codegegevens werkt, lijkt een van de minst begrepen items cyclomatische complexiteit te zijn. Met cyclomatische complexiteit zijn hogere getallen in wezen slecht en zijn lagere getallen goed. U kunt cyclomatische complexiteit gebruiken om een idee te krijgen van hoe moeilijk elke code kan zijn om fouten te testen, te onderhouden of op te lossen, evenals een indicatie van hoe waarschijnlijk de code zal zijn om fouten te produceren. Op hoog niveau bepalen we de waarde van cyclomatische complexiteit door het aantal beslissingen in uw broncode te tellen. In dit artikel begint u met een eenvoudig voorbeeld van cyclomatische complexiteit om het concept snel te begrijpen en bekijkt u vervolgens aanvullende informatie over het werkelijke gebruik en voorgestelde limieten. Ten slotte is er een sectie met bronvermeldingen die kunnen worden gebruikt om dieper in dit onderwerp te graven.

Voorbeeld

Cyclomatische complexiteit wordt gedefinieerd als het meten van de hoeveelheid beslissingslogica in een broncodefunctie NIST235. Simpel gezegd, hoe meer beslissingen moeten worden genomen in code, hoe complexer het is.

Laten we het in actie zien. Maak een nieuwe consoletoepassing en bereken onmiddellijk de metrische codegegevens door naar Analyseren > Metrische codegegevens berekenen voor Oplossing.

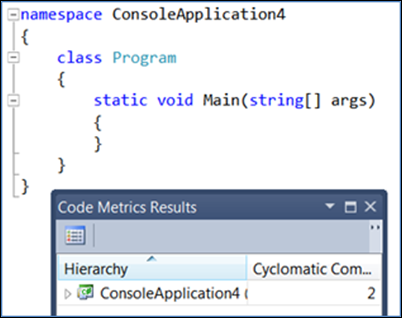
U ziet dat de cyclomatische complexiteit 2 is (de laagste waarde mogelijk). Als u niet-beslissingscode toevoegt, ziet u dat de complexiteit niet verandert:

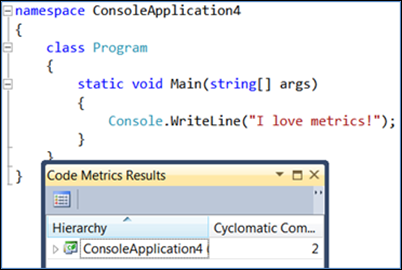
Als u een beslissing toevoegt, neemt de cyclomatische complexiteitswaarde één toe:

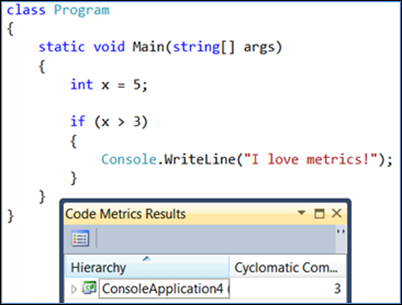
Wanneer u de if-instructie wijzigt in een switch-instructie met vier beslissingen die moeten worden genomen, gaat deze van de oorspronkelijke twee tot zes:

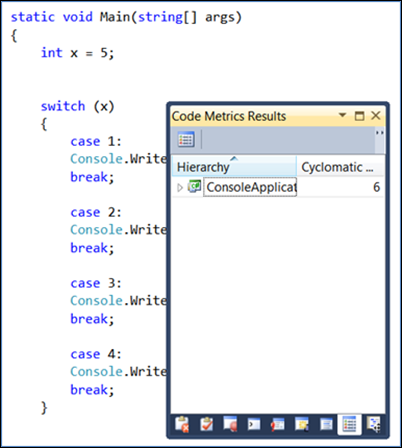
Laten we eens kijken naar een (hypothetische) grotere codebasis.

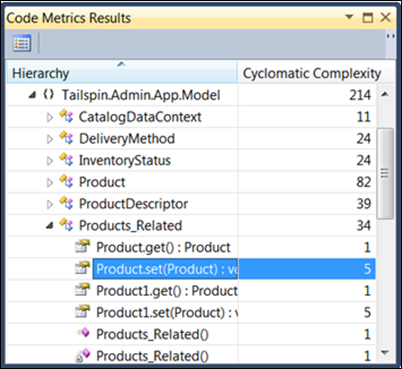
U ziet dat de meeste items, terwijl u inzoomt op de Products_Related-klasse, een waarde hebben van één, maar een paar hebben een complexiteit van vijf. Op zichzelf is dit verschil misschien geen groot probleem, maar gezien het feit dat de meeste andere leden een in dezelfde klasse hebben, moet u deze twee items zeker nader bekijken en zien wat er in hen zit. U kunt het item nader bekijken door met de rechtermuisknop op het item te klikken en Ga naar broncode te kiezen in het contextmenu. Neem een ​​nauwkeuriger kijkje naar Product.set(Product):

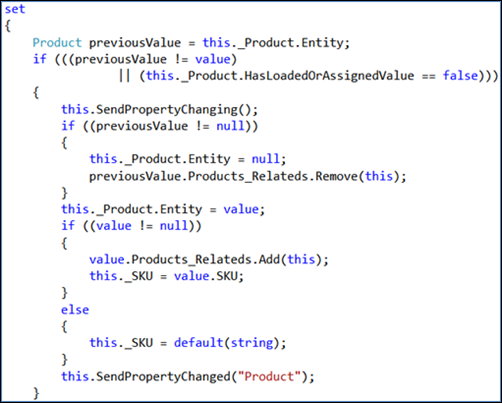
Gezien alle if-beweringen, kunt u zien waarom de cyclomatische complexiteit op een vijf is. Op dit moment kunt u besluiten dat dit resultaat een acceptabel complexiteitsniveau is, of u kunt herstructureren om de complexiteit te verminderen.

Het magicnummer

Net als bij veel metrische gegevens in deze branche is er geen exacte cyclomatische complexiteitslimiet die geschikt is voor alle organisaties. NIST235 geeft echter aan dat een limiet van 10 een goed uitgangspunt is:

"Het precieze aantal dat als limiet moet worden gebruikt, blijft echter enigszins controversieel. De oorspronkelijke limiet van 10, zoals voorgesteld door McCabe, heeft aanzienlijk bewijsmateriaal, maar de limieten van maximaal 15 zijn ook succesvol gebruikt. Limieten van meer dan 10 moeten worden gereserveerd voor projecten met verschillende operationele voordelen ten opzichte van typische projecten, zoals ervaren medewerkers, formeel ontwerp, een moderne programmeertaal, gestructureerd programmeren, code-walkthroughs en een uitgebreid testplan. Met andere woorden, een organisatie kan een complexiteitslimiet kiezen die groter is dan 10, maar alleen als het zeker weet wat het doet en bereid is om de extra testinspanningen die nodig zijn voor complexere modules te besteden." NIST235

Cyclomatische complexiteit en lijnnummers

Als je alleen kijkt naar het aantal regels code op zichzelf, is het hoogstens een zeer brede voorspeller van codekwaliteit. Er is een basis waarheid voor het idee dat hoe meer regels code in een functie, hoe waarschijnlijker het is dat er fouten optreden. Wanneer u echter cyclomatische complexiteit combineert met coderegels, hebt u een veel duidelijker beeld van het potentieel voor fouten.

Zoals beschreven door het Software Assurance Technology Center (SATC) bij NASA:

"De SATC heeft vastgesteld dat de meest effectieve evaluatie een combinatie van grootte en (cyclomatische) complexiteit is. De modules met zowel een hoge complexiteit als een grote grootte hebben meestal de laagste betrouwbaarheid. Modules met een lage grootte en hoge complexiteit vormen ook een betrouwbaarheidsrisico omdat ze meestal zeer terse code zijn, wat moeilijk te wijzigen of te wijzigen is."SATC-

Codeanalyse

Codeanalyse bevat een categorie onderhoudsregels. Zie Regels voor onderhoudbaarheidvoor meer informatie. Wanneer u verouderde codeanalyse gebruikt, bevat de regelset uitgebreide ontwerprichtlijnen een gebied voor onderhoudbaarheid:

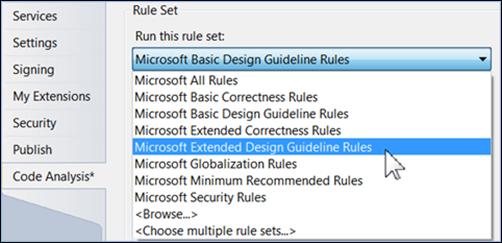
Binnen het gebied onderhoudbaarheid is een regel voor complexiteit:

Deze regel geeft een waarschuwing uit wanneer de cyclomatische complexiteit 25 bereikt, zodat u hiermee overmatige complexiteit kunt voorkomen. Zie CA1502 voor meer informatie over de regel

Alles samenbrengen

De bottom line is dat een hoog complexiteitsgetal een grotere kans op fouten betekent met een verhoogde tijd om te onderhouden en problemen op te lossen. Bekijk alle functies met een hoge complexiteit en bepaal of ze moeten worden geherstructureerd om ze minder complex te maken.

Citaten

MCCABE5

McCabe, T. en A. Watson (1994), Software Complexity (CrossTalk: The Journal of Defense Software Engineering).

NIST235

Watson, A. H., & McCabe, T. J. (1996). Gestructureerd testen: een testmethodologie met behulp van de Cyclomatic Complexity Metric (NIST Special Publication 500-235). Opgehaald op 14 mei 2011, van mccabe Software-website: http://www.mccabe.com/pdf/mccabe-nist235r.pdf

SATC

Rosenberg, L., Hammer, T., Shaw, J. (1998). Software Metrieken en Betrouwbaarheid (Proceedings of IEEE International Symposium on Software Reliability Engineering). Opgehaald op 14 mei 2011, van de website van Penn State University: https://citeseerx.ist.psu.edu/pdf/31e3f5732a7af3aecd364b6cc2a85d9495b5c159