Wat is regressie?
Regressie werkt door een relatie tot stand te brengen tussen variabelen in de gegevens die kenmerken vertegenwoordigen, ook wel de kenmerken genoemd, van het waargenomen element en de variabele die we proberen te voorspellen, ook wel het label genoemd.
Denk eraan dat ons bedrijf fietsen huurt en het verwachte aantal huurwoningen in een bepaalde dag wil voorspellen. In dit geval zijn functies onder andere de dag van de week, maand, enzovoort, terwijl het label het aantal fietsverhuur is.
Om het model te trainen, beginnen we met een gegevensvoorbeeld met de functies, evenals bekende waarden voor het label; Dus in dit geval hebben we historische gegevens nodig die datums, weersomstandigheden en het aantal fietsverhuur omvatten.
Vervolgens splitsen we dit gegevensvoorbeeld op in twee subsets:
- Een trainingsgegevensset waarop we een algoritme toepassen dat een functie bepaalt waarin de relatie tussen de functiewaarden en de bekende labelwaarden wordt ingekapseld.
- Een validatie- of testgegevensset die we kunnen gebruiken om het model te evalueren door het te gebruiken om voorspellingen voor het label te genereren en deze te vergelijken met de werkelijke bekende labelwaarden.
Het gebruik van historische gegevens met bekende labelwaarden voor het trainen van een model maakt regressie een voorbeeld van machine learning onder supervisie.
Een eenvoudig voorbeeld
Laten we een eenvoudig voorbeeld nemen om te zien hoe het trainings- en evaluatieproces in principe werkt. Stel dat we het scenario vereenvoudigen, zodat we één functie (gemiddelde dagelijkse temperatuur) gebruiken om het label voor fietsverhuur te voorspellen.
We beginnen met enkele gegevens die bekende waarden bevatten voor de gemiddelde dagelijkse temperatuurfunctie en het label voor fietsverhuur.
| Temperatuur | Verhuur |
|---|---|
| 56 | 115 |
| 61 | 126 |
| 67 | 137 |
| 72 | 140 |
| 76 | 152 |
| 82 | 156 |
| 54 | 114 |
| 62 | 129 |
We selecteren nu willekeurig vijf van deze waarnemingen en gebruiken ze om een regressiemodel te trainen. Als we het hebben over 'het trainen van een model', bedoelen we dat we een functie (een wiskundige vergelijking; we noemen het f) die de temperatuurfunctie (die we x noemen) kan gebruiken om het aantal huurwoningen te berekenen (die we y noemen). Met andere woorden, we moeten de volgende functie definiëren: f(x) = y.
Onze trainingsgegevensset ziet er als volgt uit:
| x | y |
|---|---|
| 56 | 115 |
| 61 | 126 |
| 67 | 137 |
| 72 | 140 |
| 76 | 152 |
Laten we beginnen met het tekenen van de trainingswaarden voor x en y in een grafiek:
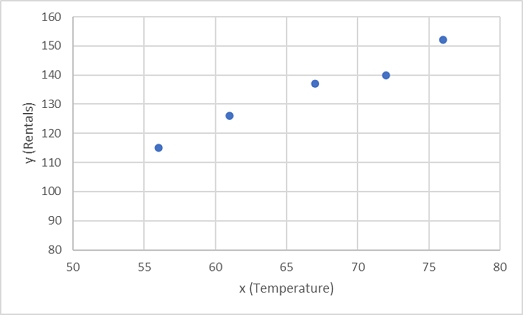
Nu moeten we deze waarden aan een functie aanpassen, waardoor er willekeurige variatie mogelijk is. U kunt waarschijnlijk zien dat de getekende punten een bijna rechte diagonale lijn vormen; Met andere woorden, er is een duidelijke lineaire relatie tussen x en y, dus we moeten een lineaire functie vinden die het meest geschikt is voor het gegevensvoorbeeld. Er zijn verschillende algoritmen die we kunnen gebruiken om deze functie te bepalen, die uiteindelijk een rechte lijn met minimale algemene variantie van de getekende punten zal vinden; aldus:
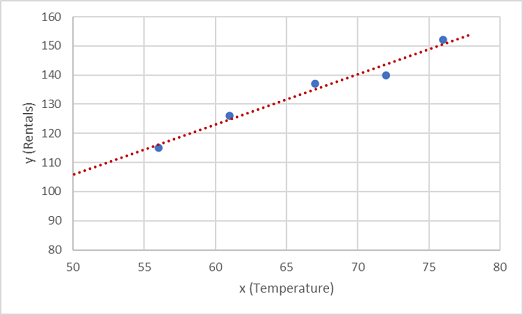
De lijn vertegenwoordigt een lineaire functie die kan worden gebruikt met een willekeurige waarde van x om de helling van de lijn en het snijpunt ervan toe te passen (waarbij de lijn de y-as overschrijdt wanneer x 0 is) om y te berekenen. In dit geval, als we de lijn naar links uitbreidt, vinden we dat wanneer x 0 is, y ongeveer 20 is en de helling van de lijn zodanig is dat voor elke eenheid van x u naar rechts gaat, y met ongeveer 1,7 toeneemt. Daarom kunnen we onze f-functie berekenen als 20 + 1,7x.
Nu we onze voorspellende functie hebben gedefinieerd, kunnen we deze gebruiken om labels te voorspellen voor de validatiegegevens die we hebben vastgehouden en de voorspelde waarden te vergelijken (die we meestal aangeven met het symbool ŷ of 'y-hat') met de werkelijke bekende y-waarden.
| x | y | ŷ |
|---|---|---|
| 82 | 156 | 159.4 |
| 54 | 114 | 111.8 |
| 62 | 129 | 125.4 |
Laten we eens kijken hoe de waarden y en ŷ in een plot worden vergeleken:
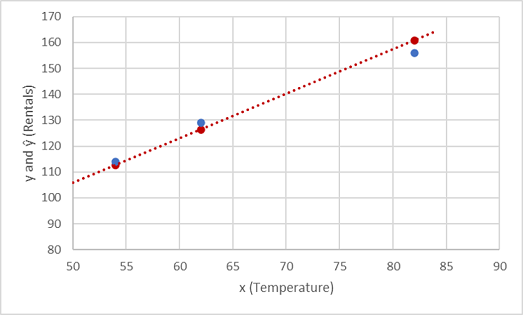
De getekende punten op de functielijn zijn de voorspelde ŷ waarden die door de functie worden berekend en de andere getekende punten zijn de werkelijke y-waarden.
Er zijn verschillende manieren waarop we de variantie tussen de voorspelde en werkelijke waarden kunnen meten en we kunnen deze metrische gegevens gebruiken om te evalueren hoe goed het model voorspelt.
Notitie
Machine learning is gebaseerd op statistieken en wiskunde en het is belangrijk om rekening te houden met specifieke termen die statistici en wiskundigen (en daarom gegevenswetenschappers) gebruiken. U kunt het verschil zien tussen een voorspelde labelwaarde en de werkelijke labelwaarde als een meting van de fout. In de praktijk zijn de werkelijke waarden echter gebaseerd op steekproefobservaties (die zelf kunnen worden onderworpen aan een willekeurige variantie). Om duidelijk te maken dat we een voorspelde waarde (ŷ) vergelijken met een waargenomen waarde (y) verwijzen we naar het verschil tussen deze waarden als de residuen. We kunnen de residuen voor alle voorspellingen van validatiegegevens samenvatten om het totale verlies in het model te berekenen als meting van de voorspellende prestaties.
Een van de meest voorkomende manieren om het verlies te meten, is het kwadrateren van de afzonderlijke residuen, het optellen van de kwadraten en het gemiddelde berekenen. Het kwadraten van de residuen heeft het effect van het baseren van de berekening op absolute waarden (waarbij wordt genegeerd of het verschil negatief of positief is) en meer gewicht krijgt bij grotere verschillen. Deze metrische waarde wordt de gemiddelde kwadratische fout genoemd.
Voor onze validatiegegevens ziet de berekening er als volgt uit:
| y | ŷ | y - ŷ | (y - ŷ)2 |
|---|---|---|---|
| 156 | 159.4 | -3.4 | 11.56 |
| 114 | 111.8 | 2.2 | 4,84 |
| 129 | 125.4 | 3,6 | 12.96 |
| Sum | ∑ | 29.36 | |
| Gemiddelde | x̄ | 9.79 |
Daarom is het verlies voor ons model op basis van de MSE-meetwaarde 9,79.
Dus, is dat goed? Het is moeilijk te vertellen, omdat de MSE-waarde niet wordt uitgedrukt in een zinvolle maateenheid. We weten wel dat hoe lager de waarde is, hoe minder verlies er is in het model, en daarom, hoe beter het voorspelt. Dit maakt het een handige metrische waarde om twee modellen te vergelijken en het model te vinden dat het beste presteert.
Soms is het handiger om het verlies in dezelfde maateenheid uit te drukken als de voorspelde labelwaarde zelf; in dit geval het aantal huurwoningen. Het is mogelijk om dit te doen door de vierkantswortel van de MSE te berekenen, die een bekende metriek produceert, niet verrassend, als de RMSE (Root Mean Squared Error).
√9,79 = 3,13
De RMSE van ons model geeft dus aan dat het verlies iets meer dan 3 is, wat u losjes kunt interpreteren, wat betekent dat gemiddeld onjuiste voorspellingen door ongeveer drie verhuurfouten zijn.
Er zijn veel andere metrische gegevens die kunnen worden gebruikt om verlies in een regressie te meten. R 2 (R-Kwadraat) (ook wel bekend als de bepalingscoëfficiënt) is bijvoorbeeld de correlatie tussen x en y kwadraat. Dit produceert een waarde tussen 0 en 1 die de hoeveelheid variantie meet die door het model kan worden verklaard. Over het algemeen is deze waarde dichter bij 1, hoe beter het model voorspelt.