Concepten van deep neurale netwerken
Voordat u gaat verkennen hoe u een DNN-machine learning-model (Deep Neural Network) traint, gaan we nadenken over wat we proberen te bereiken. Machine learning houdt zich bezig met het voorspellen van een label op basis van bepaalde kenmerken van een bepaalde observatie. In eenvoudige termen is een machine learning-model een functie die y (het label) berekent van x (de functies): f(x)=y.
Een voorbeeld van een eenvoudige classificatie
Stel dat uw observatie bestaat uit enkele metingen van een pinguïn.

De metingen zijn met name:
- De lengte van de rekening van de pinguïn.
- De diepte van de rekening van de pinguïn.
- De lengte van de pinguïn's flipper.
- Het gewicht van de pinguïn.
In dit geval zijn de kenmerken (x) een vector van vier waarden, of wiskundig, x=[x1,x 2,x 3,x 4].
Stel dat het label dat we proberen te voorspellen (y) de soort van de pinguïn is en dat er drie mogelijke soorten kunnen zijn:
- Adelie
- Ezelspinguïn
- Chinstrap
Dit is een voorbeeld van een classificatieprobleem , waarin het machine learning-model de meest waarschijnlijke klasse moet voorspellen waartoe de observatie behoort. Een classificatiemodel doet dit door een label te voorspellen dat bestaat uit de waarschijnlijkheid voor elke klasse. Met andere woorden: y is een vector van drie waarschijnlijkheidswaarden; één voor elk van de mogelijke klassen: y=[P(0),P(1),P(2)].
U traint het machine learning-model met behulp van waarnemingen waarvoor u het ware label al kent. U hebt bijvoorbeeld de volgende functiemetingen voor een Adelie-exemplaar :
x=[37.3, 16.8, 19.2, 30.0]
U weet al dat dit een voorbeeld is van een Adelie (klasse 0), dus een perfecte classificatiefunctie moet resulteren in een label dat een kans van 100% voor klasse 0 aangeeft en een 0% kans voor klassen 1 en 2:
y=[1, 0, 0]
Een deep neural netwerkmodel
Hoe zouden we deep learning gebruiken om een classificatiemodel te bouwen voor het pinguïnclassificatiemodel? Laten we eens een voorbeeld bekijken:
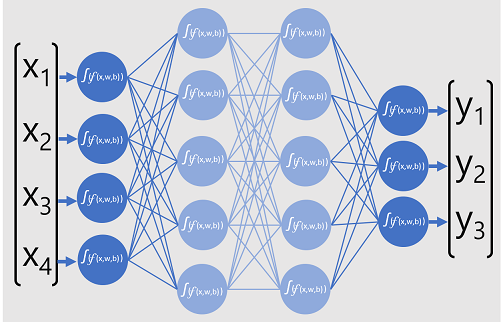
Het deep neurale netwerkmodel voor de classificatie bestaat uit meerdere lagen kunstmatige neuronen. In dit geval zijn er vier lagen:
- Een invoerlaag met een neuron voor elke verwachte invoerwaarde (x).
- Twee zogenaamde verborgen lagen, elk met vijf neuronen.
- Een uitvoerlaag met drie neuronen: één voor elke klassekanswaarde (y) die door het model moet worden voorspeld.
Vanwege de gelaagde architectuur van het netwerk wordt dit type model soms een multilaags perceptron genoemd. Bovendien ziet u dat alle neuronen in de invoer- en verborgen lagen zijn verbonden met alle neuronen in de volgende lagen- dit is een voorbeeld van een volledig verbonden netwerk.
Wanneer u een model zoals dit maakt, moet u een invoerlaag definiëren die ondersteuning biedt voor het aantal functies dat uw model gaat verwerken en een uitvoerlaag die overeenkomt met het aantal uitvoer dat u verwacht te produceren. U kunt bepalen hoeveel verborgen lagen u wilt opnemen en hoeveel neuronen er in elk van deze zijn; maar u hebt geen controle over de invoer- en uitvoerwaarden voor deze lagen. Deze worden bepaald door het modeltrainingsproces.
Een diep neuraal netwerk trainen
Het trainingsproces voor een diep neuraal netwerk bestaat uit meerdere iteraties, epochs genoemd. Voor het eerste tijdvak begint u met het toewijzen van willekeurige initialisatiewaarden voor het gewicht (w) en bias b-waarden. Vervolgens is het proces als volgt:
- Functies voor gegevensobservaties met bekende labelwaarden worden verzonden naar de invoerlaag. Over het algemeen worden deze waarnemingen gegroepeerd in batches (ook wel minibatches genoemd).
- De neuronen passen vervolgens hun functie toe en indien geactiveerd, geven het resultaat door aan de volgende laag totdat de uitvoerlaag een voorspelling produceert.
- De voorspelling wordt vergeleken met de werkelijke bekende waarde en de hoeveelheid variantie tussen de voorspelde en werkelijke waarden (die we het verlies noemen) wordt berekend.
- Op basis van de resultaten worden herziene waarden voor de gewichten en vooroordelen berekend om het verlies te verminderen en deze aanpassingen worden teruggepropageerd aan de neuronen in de netwerklagen.
- In het volgende tijdvak wordt de batchtrainingsdoorgang herhaald met de herziene gewichts- en vooroordelenwaarden, waardoor hopelijk de nauwkeurigheid van het model wordt verbeterd (door het verlies te verminderen).
Notitie
Het verwerken van de trainingsfuncties als een batch verbetert de efficiëntie van het trainingsproces door meerdere waarnemingen tegelijkertijd te verwerken als een matrix van kenmerken met vectoren van gewichten en vooroordelen. Lineaire algebraïsche functies die werken met matrices en vectoren, zijn ook beschikbaar in 3D-grafische verwerking. Daarom bieden computers met gpu's (graphic processing units) aanzienlijk betere prestaties voor deep learning-modeltraining dan alleen computers met een centrale verwerkingseenheid (CPU).
Een beter overzicht van verliesfuncties en backpropagation
In de vorige beschrijving van het deep learning-trainingsproces werd vermeld dat het verlies van het model wordt berekend en wordt gebruikt om de gewichts- en vooroordelenwaarden aan te passen. Hoe werkt dit precies?
Verlies berekenen
Stel dat een van de monsters die tijdens het trainingsproces zijn doorgegeven, kenmerken van een Adelie-exemplaar (klasse 0) bevat. De juiste uitvoer van het netwerk is [1, 0, 0]. Stel nu dat de uitvoer die door het netwerk wordt geproduceerd [0.4, 0.3, 0.3] is. Als u deze waarden vergelijkt, kunnen we een absolute variantie voor elk element berekenen (met andere woorden, hoe ver is elke voorspelde waarde weg van wat deze moet zijn) als [0,6, 0,3, 0,3].
Omdat we eigenlijk te maken hebben met meerdere waarnemingen, aggregeren we meestal de variantie, bijvoorbeeld door de afzonderlijke variantiewaarden te kwadraten en het gemiddelde te berekenen, dus eindigen we met één gemiddelde verlieswaarde, zoals 0,18.
Optimalisaties
Hier is de slimme bit. Het verlies wordt berekend met behulp van een functie, die werkt op de resultaten van de laatste laag van het netwerk, wat ook een functie is. De laatste netwerklaag werkt op de uitvoer van de vorige lagen, die ook functies zijn. Dus in feite is het hele model van de invoerlaag tot aan de verliesberekening slechts één grote geneste functie. Functies hebben een aantal zeer nuttige kenmerken, waaronder:
- U kunt een functie conceptueel maken als een getekende lijn, waarbij de uitvoer wordt vergeleken met elk van de variabelen.
- U kunt differentiële calculus gebruiken om op elk gewenst moment de afgeleide van de functie te berekenen met betrekking tot de variabelen.
Laten we de eerste van deze mogelijkheden nemen. We kunnen de lijn van de functie uitzetten om te laten zien hoe een afzonderlijke gewichtswaarde zich verhoudt tot verlies en op die regel het punt markeren waarop de huidige gewichtswaarde overeenkomt met de huidige verlieswaarde.
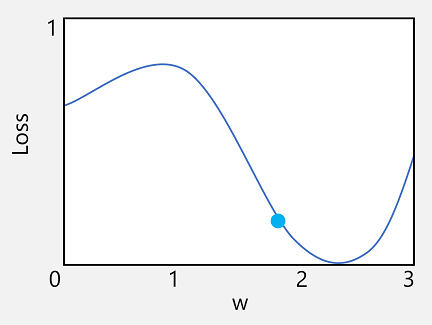
Nu gaan we het tweede kenmerk van een functie toepassen. De afgeleide van een functie voor een bepaald punt geeft aan of de helling (of gradiënt) van de functie-uitvoer (in dit geval verlies) toeneemt of afneemt ten opzichte van een functievariabele (in dit geval de gewichtswaarde). Een positieve afgeleide geeft aan dat de functie toeneemt en een negatieve afgeleide geeft aan dat deze afneemt. In dit geval heeft de functie op het uitgezet punt voor de huidige gewichtswaarde een neerwaartse kleurovergang. Met andere woorden, het verhogen van het gewicht zal het effect hebben van het verminderen van het verlies.
We gebruiken een optimizer om dezelfde truc toe te passen voor alle gewichts- en vooroordelenvariabelen in het model en bepalen in welke richting we ze moeten aanpassen (omhoog of omlaag) om de totale hoeveelheid verlies in het model te verminderen. Er zijn meerdere veelgebruikte optimalisatiealgoritmen, waaronder stochastische gradiëntafname (SGD), Adaptive Learning Rate (ADADELTA), Adaptive Momentum Estimation (Adam) en andere, die allemaal zijn ontworpen om erachter te komen hoe de gewichten en vooroordelen kunnen worden aangepast om verlies te minimaliseren.
Leersnelheid
Nu is de voor de hand liggende volgende vraag, door hoeveel moet de optimizer de gewichten en vooroordelenwaarden aanpassen? Als u naar de plot kijkt voor onze gewichtswaarde, kunt u zien dat het verhogen van het gewicht met een kleine hoeveelheid de functielijn omlaag zal volgen (het verlies verminderen), maar als we het met te veel verhogen, begint de functielijn weer omhoog te gaan, zodat we het verlies daadwerkelijk kunnen verhogen; en na het volgende tijdvak kunnen we vinden dat we het gewicht moeten verminderen.
De grootte van de aanpassing wordt bepaald door een parameter die u hebt ingesteld voor de training, de leersnelheid. Een lage leersnelheid resulteert in kleine aanpassingen (zodat het langer kan duren om het verlies te minimaliseren), terwijl een hoog leerpercentage resulteert in grote aanpassingen (zodat u het minimum helemaal mist).