Classificatiemodellen evalueren
De nauwkeurigheid van de training van een classificatiemodel is veel minder belangrijk dan hoe goed dat model werkt wanneer nieuwe, ongelezen gegevens worden gegeven. We trainen immers modellen zodat ze kunnen worden gebruikt op nieuwe gegevens die we in de echte wereld vinden. Dus nadat we een classificatiemodel hebben getraind, evalueren we hoe het presteert op een set nieuwe, ongelezen gegevens.
In de vorige eenheden hebben we een model gemaakt dat zou voorspellen of een patiënt diabetes had of niet op basis van hun bloedglucosegehalte. Wanneer deze worden toegepast op bepaalde gegevens die geen deel uitmaken van de trainingsset, krijgen we de volgende voorspellingen.
| x | y | ŷ |
|---|---|---|
| 83 | 0 | 0 |
| 119 | 1 | 1 |
| 104 | 1 | 0 |
| 105 | 0 | 1 |
| 86 | 0 | 0 |
| 109 | 1 | 1 |
Zoals u weet, verwijst x naar het bloedglucoseniveau, y verwijst naar of ze daadwerkelijk diabetisch zijn en ŷ verwijst naar de voorspelling van het model of ze diabetisch zijn of niet.
Alleen maar berekenen hoeveel voorspellingen juist zijn, is soms misleidend of te simplistisch voor ons om inzicht te krijgen in de soorten fouten die het zal maken in de echte wereld. Voor meer gedetailleerde informatie kunnen we de resultaten in een structuur met de naam verwarringsmatrix in een tabel opvragen, zoals deze:
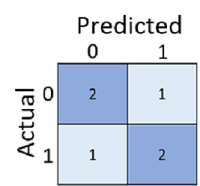
De verwarringsmatrix toont het totale aantal gevallen waarin:
- Het model voorspelde 0 en het werkelijke label is 0 (terecht negatieven, linksboven)
- Het model voorspelde 1 en het werkelijke label is 1 (terecht positieven, rechtsonder)
- Het model voorspelde 0 en het werkelijke label is 1 (fout-negatieven, linksonder)
- Het model voorspeld 1 en het werkelijke label is 0 (fout-positieven, rechtsboven)
De cellen in een verwarringsmatrix worden vaak gearceerd, zodat hogere waarden een diepere tint hebben. Dit maakt het gemakkelijker om een sterke diagonale trend te zien van linksboven naar rechtsonder, waarbij de cellen worden gemarkeerd waar de voorspelde waarde en werkelijke waarde hetzelfde zijn.
Op basis van deze kernwaarden kunt u een bereik van andere metrische gegevens berekenen waarmee u de prestaties van het model kunt evalueren. Voorbeeld:
- Nauwkeurigheid: (TP+TN)/(TP+TN+FP+FN) - uit alle voorspellingen, hoeveel waren er correct?
- Relevante overeenkomsten: TP/(TP+FN) - van alle gevallen die positief zijn , hoeveel heeft het model geïdentificeerd?
- Precisie: TP/(TP+FP) - van alle gevallen waarin het model voorspelde positief te zijn, hoeveel zijn er daadwerkelijk positief?