Deep learning
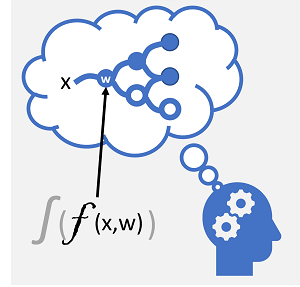
Deep learning is een geavanceerde vorm van machine learning die probeert de manier te emuleren waarop het menselijk brein leert. De sleutel tot deep learning is het creëren van een kunstmatig neuraal netwerk dat elektrochemische activiteit in biologische neuronen simuleert met behulp van wiskundige functies, zoals hier wordt weergegeven.
| Biologisch neuraal netwerk | Kunstmatig neuraal netwerk |
|---|---|

|
|
| Neuronen branden als reactie op elektrochemische prikkels. Wanneer het wordt geactiveerd, wordt het signaal doorgegeven aan verbonden neuronen. | Elke neuron is een functie die werkt op een invoerwaarde (x) en een gewicht (w). De functie wordt verpakt in een activeringsfunctie die bepaalt of de uitvoer moet worden doorgegeven. |
Kunstmatige neurale netwerken bestaan uit meerdere lagen van neuronen - in wezen een diep geneste functie definiëren. Deze architectuur is de reden waarom de techniek wordt aangeduid als deep learning en de modellen die hiermee worden geproduceerd, worden vaak aangeduid als deep neural networks (DNN's). U kunt diepe neurale netwerken gebruiken voor veel soorten machine learning-problemen, waaronder regressie en classificatie, evenals meer gespecialiseerde modellen voor natuurlijke taalverwerking en computer vision.
Net als bij andere machine learning-technieken die in deze module worden besproken, omvat deep learning het aanpassen van trainingsgegevens aan een functie die een label (y) kan voorspellen op basis van de waarde van een of meer functies (x). De functie (f(x)) is de buitenste laag van een geneste functie waarin elke laag van het neurale netwerk functies bevat die op x werken en de gewichtswaarden (w) die eraan zijn gekoppeld. Het algoritme dat wordt gebruikt om het model te trainen, omvat het iteratief invoeren van de functiewaarden (x) in de trainingsgegevens door de lagen om uitvoerwaarden voor ŷ te berekenen, en het model te valideren om te evalueren hoe ver de berekende ŷ-waarden af liggen van de bekende y-waarden (die het foutniveau of verlies in het model kwantificeren), en wijzigt u vervolgens het gewicht (w) om het verlies te verminderen. Het getrainde model bevat de uiteindelijke gewichtswaarden die resulteren in de meest nauwkeurige voorspellingen.
Voorbeeld: deep learning gebruiken voor classificatie
Om beter te begrijpen hoe een deep neural network model werkt, gaan we een voorbeeld bekijken waarin een neuraal netwerk wordt gebruikt om een classificatiemodel voor pinguïnsoorten te definiëren.
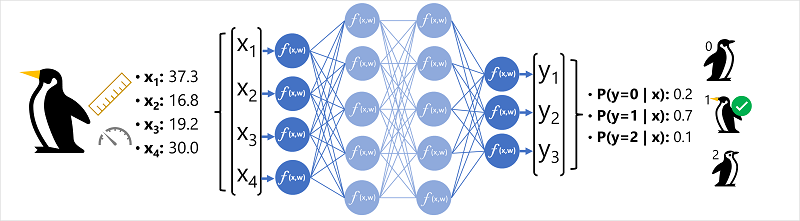
De functiegegevens (x) bestaan uit enkele metingen van een pinguïn. De metingen zijn met name:
- De lengte van de slang van de pinguïn.
- De diepte van de pinguïns.
- De lengte van de flippers van de pinguïn.
- Het gewicht van de pinguïn.
In dit geval is x een vector van vier waarden, of wiskundig gezien, x=[x1,x2,x3,x4].
Het label dat we proberen te voorspellen (y) is de soort van de pinguïn en dat er drie mogelijke soorten zijn:
- Adelie
- Gentoo
- Chinstrap
Dit is een voorbeeld van een classificatieprobleem, waarbij het machine learning-model de meest waarschijnlijke klasse moet voorspellen waartoe een observatie behoort. Een classificatiemodel bereikt dit door een label te voorspellen dat bestaat uit de waarschijnlijkheid voor elke klasse. Met andere woorden, y is een vector van drie waarschijnlijkheidswaarden; één voor elk van de mogelijke klassen: [P(y=0|x), P(y=1|x), P(y=2|x)].
Het proces voor het deducteren van een voorspelde pinguïnklasse met behulp van dit netwerk is:
- De functievector voor een pinguïnobservatie wordt ingevoerd in de invoerlaag van het neurale netwerk, die bestaat uit een neuron voor elke x-waarde . In dit voorbeeld wordt de volgende x-vector gebruikt als invoer: [37.3, 16.8, 19.2, 30.0]
- De functies voor de eerste laag van neuronen berekenen elk een gewogen som door de x-waarde en het gewicht w te combineren en deze door te geven aan een activeringsfunctie die bepaalt of deze voldoet aan de drempelwaarde die moet worden doorgegeven aan de volgende laag.
- Elke neuron in een laag is verbonden met alle neuronen in de volgende laag (een architectuur die ook wel een volledig verbonden netwerk wordt genoemd), dus de resultaten van elke laag worden doorgestuurd via het netwerk totdat ze de uitvoerlaag bereiken.
- De uitvoerlaag produceert een vector van waarden; in dit geval met behulp van een softmax of een vergelijkbare functie om de kansverdeling voor de drie mogelijke klassen pinguïn te berekenen. In dit voorbeeld is de uitvoervector: [0.2, 0.7, 0.1]
- De elementen van de vector vertegenwoordigen de waarschijnlijkheden voor de klassen 0, 1 en 2. De tweede waarde is de hoogste, dus het model voorspelt dat de soort van de pinguïn 1 is (Gentoo).
Hoe leert een neuraal netwerk?
De gewichten in een neuraal netwerk staan centraal bij de berekening van voorspelde waarden voor labels. Tijdens het trainingsproces leert het model de gewichten die resulteren in de meest nauwkeurige voorspellingen. Laten we het trainingsproces wat gedetailleerder verkennen om te begrijpen hoe dit leren plaatsvindt.
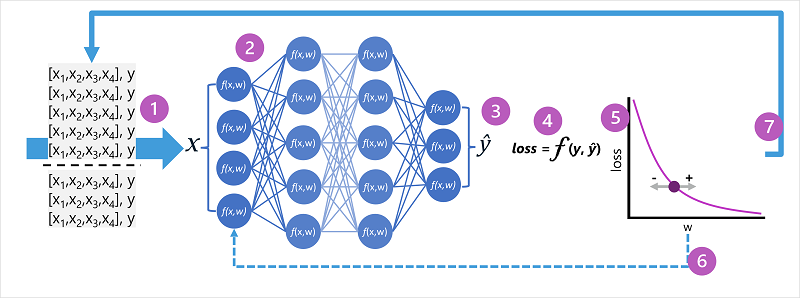
- De gegevenssets voor training en validatie worden gedefinieerd en de trainingsfuncties worden ingevoerd in de invoerlaag.
- De neuronen in elke laag van het netwerk passen hun gewicht toe (die in eerste instantie willekeurig worden toegewezen) en voeren de gegevens via het netwerk.
- De uitvoerlaag produceert een vector met de berekende waarden voor ŷ. Een uitvoer voor een pinguïnklassevoorspelling kan bijvoorbeeld [0,3 zijn. 0.1. 0.6].
- Een loss-functie wordt gebruikt om de voorspelde ŷ-waarden te vergelijken met de bekende y-waarden en het verschil samen te voegen (dit wordt het verlies genoemd). Als de bekende klasse voor de case die de uitvoer in de vorige stap heeft geretourneerd bijvoorbeeld Chinstrap is, moet de y-waarde[0,0, 0,0, 1,0] zijn. Het absolute verschil tussen deze en de ŷ vector is [0,3, 0,1, 0,4]. In werkelijkheid berekent de functie loss de aggregatievariantie voor meerdere gevallen en vat deze samen als één verlieswaarde .
- Omdat het hele netwerk in wezen één grote geneste functie is, kan een optimalisatiefunctie differentiële analyse gebruiken om de invloed van elk gewicht in het netwerk op het verlies te evalueren en te bepalen hoe ze kunnen worden aangepast (omhoog of omlaag) om het totale verlies te verminderen. De specifieke optimalisatietechniek kan variëren, maar meestal gaat het om een benadering van gradiëntafname waarbij elk gewicht wordt verhoogd of verlaagd om het verlies te minimaliseren.
- De wijzigingen in de gewichten worden terugpropageerd naar de lagen in het netwerk, waarbij de eerder gebruikte waarden worden vervangen.
- Het proces wordt herhaald over meerdere iteraties (ook wel tijdvakken genoemd) totdat het verlies wordt geminimaliseerd en het model acceptabel nauwkeurig voorspelt.
Notitie
Hoewel het gemakkelijker is om elk geval te bedenken in de trainingsgegevens die één voor één door het netwerk worden doorgegeven, worden de gegevens in werkelijkheid in batches in matrices verwerkt met behulp van lineaire algebraïsche berekeningen. Daarom wordt neurale netwerktraining het beste uitgevoerd op computers met GPU's (grafische verwerkingseenheden) die zijn geoptimaliseerd voor vector- en matrixmanipulatie.