Classificatie met meerdere klassen
Classificatie met meerdere klassen wordt gebruikt om te voorspellen welke van meerdere mogelijke klassen een observatie behoort. Als een machine learning-techniek onder supervisie volgt deze dezelfde iteratieve training, validatie en evaluatieproces als regressie en binaire classificatie waarin een subset van de trainingsgegevens wordt vastgehouden om het getrainde model te valideren.
Voorbeeld: classificatie met meerdere klassen
Classificatiealgoritmen met meerdere klassen worden gebruikt om waarschijnlijkheidswaarden voor meerdere klasselabels te berekenen, zodat een model de meest waarschijnlijke klasse voor een bepaalde observatie kan voorspellen.
Laten we een voorbeeld bekijken waarin we enkele waarnemingen van pinguïns hebben, waarin de lengte van de flipper (x) van elke pinguïn wordt vastgelegd. Voor elke waarneming omvatten de gegevens de pinguïnsoorten (y), die als volgt worden gecodeerd:
- 0: Adelie
- 1: Gentoo
- 2: Chinstrap
Notitie
Net als bij eerdere voorbeelden in deze module zou een echt scenario meerdere functiewaarden (x) bevatten. We gebruiken één functie om alles eenvoudig te houden.
 |
 |
|---|---|
| Lengte van flipper (x) | Soorten (y) |
| 167 | 0 |
| 172 | 0 |
| 225 | 2 |
| 197 | 1 |
| 189 | 1 |
| 232 | 2 |
| 158 | 0 |
Een classificatiemodel met meerdere klassen trainen
Als u een classificatiemodel met meerdere klassen wilt trainen, moet u een algoritme gebruiken om de trainingsgegevens aan te passen aan een functie waarmee een waarschijnlijkheidswaarde voor elke mogelijke klasse wordt berekend. Er zijn twee soorten algoritmes die u kunt gebruiken om dit te doen:
- OvR-algoritmen (One-vs-Rest)
- Multinomiale algoritmen
OvR-algoritmen (One-vs-Rest)
Met een-vs-Rest-algoritmen wordt voor elke klasse een binaire classificatiefunctie getraind, waarbij elke berekening de kans op de waarneming een voorbeeld is van de doelklasse. Elke functie berekent de kans dat de observatie een specifieke klasse is vergeleken met een andere klasse. Voor ons classificatiemodel voor pinguïn-soorten zou het algoritme in feite drie binaire classificatiefuncties maken:
- f0(x) = P(y=0 | x)
- f1(x) = P(y=1 | x)
- f2(x) = P(y=2 | x)
Elk algoritme produceert een sigmoid-functie die een waarschijnlijkheidswaarde tussen 0,0 en 1,0 berekent. Een model dat is getraind met dit type algoritme voorspelt de klasse voor de functie die de hoogste waarschijnlijkheidsuitvoer produceert.
Multinomiale algoritmen
Als alternatief is het gebruik van een multinomiaal algoritme, waarmee één functie wordt gemaakt die een uitvoer met meerdere waarden retourneert. De uitvoer is een vector (een matrix met waarden) die de waarschijnlijkheidsverdeling voor alle mogelijke klassen bevat, met een waarschijnlijkheidsscore voor elke klasse die bij totalen tot 1,0 is opgetellen:
f(x) =[P(y=0|x), P(y=1|x), P(y=2|x)]
Een voorbeeld van dit soort functie is een softmax-functie , die een uitvoer kan produceren zoals in het volgende voorbeeld:
[0.2, 0.3, 0.5]
De elementen in de vector vertegenwoordigen respectievelijk de waarschijnlijkheden voor klassen 0, 1 en 2; in dit geval is de klasse met de hoogste waarschijnlijkheid 2.
Ongeacht welk type algoritme wordt gebruikt, gebruikt het model de resulterende functie om de meest waarschijnlijke klasse voor een bepaalde set functies (x) te bepalen en het bijbehorende klasselabel (y) te voorspellen.
Een classificatiemodel met meerdere klassen evalueren
U kunt een classificatie met meerdere klassen evalueren door metrische gegevens voor binaire classificatie voor elke afzonderlijke klasse te berekenen. U kunt ook statistische metrische gegevens berekenen die rekening houden met alle klassen.
We gaan ervan uit dat we onze classificatie met meerdere klassen hebben gevalideerd en de volgende resultaten hebben verkregen:
| Lengte van flipper (x) | Werkelijke soorten (y) | Voorspelde soorten (ŷ) |
|---|---|---|
| 165 | 0 | 0 |
| 171 | 0 | 0 |
| 205 | 2 | 1 |
| 195 | 1 | 1 |
| 183 | 1 | 1 |
| 221 | 2 | 2 |
| 214 | 2 | 2 |
De verwarringsmatrix voor een classificatie met meerdere klassen is vergelijkbaar met die van een binaire classificatie, met uitzondering van het aantal voorspellingen voor elke combinatie van voorspelde (ŷ) en werkelijke klasselabels (y):
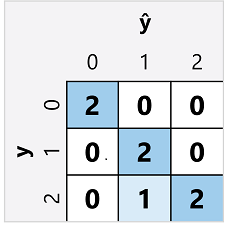
In deze verwarringsmatrix kunnen we de metrische gegevens voor elke afzonderlijke klasse als volgt bepalen:
| Klas | TP | TN | FP | FN | Nauwkeurigheid | Intrekken | Precisie | F1-Score |
|---|---|---|---|---|---|---|---|---|
| 0 | 2 | 5 | 0 | 0 | 1.0 | 1.0 | 1.0 | 1.0 |
| 1 | 2 | 4 | 1 | 0 | 0,86 | 1.0 | 0.67 | 0,8 |
| 2 | 2 | 4 | 0 | 1 | 0,86 | 0.67 | 1.0 | 0,8 |
Als u de metrische gegevens voor algemene nauwkeurigheid, relevante overeenkomsten en precisie wilt berekenen, gebruikt u het totaal van de metrische gegevens TP, TN, FP en FN :
- Algehele nauwkeurigheid = (13+6)÷(13+6+1+1) = 0,90
- Algemene relevante overeenkomsten = 6÷(6+1) = 0,86
- Totale precisie = 6÷(6+1) = 0,86
De algehele F1-score wordt berekend met behulp van de algemene metrische gegevens voor relevante overeenkomsten en precisie:
- Totale F1-score = (2x0,86x0.86)÷(0,86+0,86) = 0,86