Binaire classificatie
Classificatie, zoals regressie, is een machine learning-techniek onder supervisie en volgt daarom hetzelfde iteratieve proces voor het trainen, valideren en evalueren van modellen. In plaats van numerieke waarden zoals een regressiemodel te berekenen, berekenen de algoritmen die worden gebruikt voor het trainen van classificatiemodellen waarschijnlijkheidswaarden voor klassetoewijzing en de metrische evaluatiegegevens die worden gebruikt om de modelprestaties te evalueren, de voorspelde klassen met de werkelijke klassen.
Binaire classificatiealgoritmen worden gebruikt om een model te trainen dat een van de twee mogelijke labels voor één klasse voorspelt. In wezen voorspelt u waar of onwaar. In de meeste echte scenario's bestaan de gegevensobservaties die worden gebruikt voor het trainen en valideren van het model uit meerdere functiewaarden (x) en een y-waarde die 1 of 0 is.
Voorbeeld: binaire classificatie
Als u wilt weten hoe binaire classificatie werkt, gaan we een vereenvoudigd voorbeeld bekijken waarin één functie (x) wordt gebruikt om te voorspellen of het label y 1 of 0 is. In dit voorbeeld gebruiken we het bloedglucoseniveau van een patiënt om te voorspellen of de patiënt diabetes heeft. Hier volgen de gegevens waarmee we het model gaan trainen:
 |
 |
|---|---|
| Bloedglucose (x) | Diabetische? (y) |
| 67 | 0 |
| 103 | 1 |
| 114 | 1 |
| 72 | 0 |
| 116 | 1 |
| 65 | 0 |
Een binair classificatiemodel trainen
Om het model te trainen, gebruiken we een algoritme om de trainingsgegevens aan te passen aan een functie waarmee de kans wordt berekend dat het klasselabel waar is (met andere woorden, dat de patiënt diabetes heeft). De kans wordt gemeten als een waarde tussen 0,0 en 1,0, zodat de totale kans voor alle mogelijke klassen 1,0 is. Als de kans op een patiënt met diabetes bijvoorbeeld 0,7 is, is er een overeenkomstige kans van 0,3 dat de patiënt niet diabetisch is.
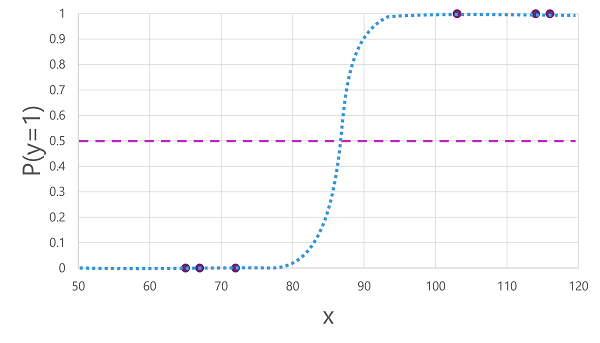
Er zijn veel algoritmen die kunnen worden gebruikt voor binaire classificatie, zoals logistieke regressie, die een sigmoid-functie (S-vormig) afleiden met waarden tussen 0,0 en 1.0, zoals deze:
Notitie
Ondanks de naam wordt in machine learning logistieke regressie gebruikt voor classificatie, niet regressie. Het belangrijkste punt is de logistieke aard van de functie die het produceert, die een S-vormige curve beschrijft tussen een lagere en hogere waarde (0,0 en 1,0 bij gebruik voor binaire classificatie).
De functie die door het algoritme wordt geproduceerd, beschrijft de kans dat y waar is (y=1) voor een bepaalde waarde van x. Wiskundig kunt u de functie als volgt uitdrukken:
f(x) = P(y=1 | x)
Voor drie van de zes waarnemingen in de trainingsgegevens weten we dat y zeker waar is, dus de waarschijnlijkheid voor die waarnemingen dat y=1 1,0 is en voor de andere drie weten we dat y zeker onwaar is, dus de kans dat y=1 0,0 is. De S-vormige curve beschrijft de waarschijnlijkheidsverdeling, zodat een waarde van x op de lijn wordt weergegeven met de overeenkomende waarschijnlijkheid die y 1 is.
Het diagram bevat ook een horizontale lijn om de drempelwaarde aan te geven waarmee een model op basis van deze functie waar (1) of onwaar (0) voorspelt. De drempelwaarde ligt op het middelpunt van y (P(y) = 0,5. Voor waarden op dit punt of hoger voorspelt het model waar (1). Voor waarden onder dit punt voorspelt het onwaar (0). Voor een patiënt met een bloedglucosegehalte van 90 zou de functie bijvoorbeeld resulteren in een waarschijnlijkheidswaarde van 0,9. Omdat 0,9 hoger is dan de drempelwaarde van 0,5, zou het model waar voorspellen (1), met andere woorden, de patiënt wordt voorspeld diabetes te hebben.
Een binair classificatiemodel evalueren
Net als bij regressie houdt u bij het trainen van een binair classificatiemodel een willekeurige subset met gegevens vast waarmee het getrainde model moet worden gevalideerd. We gaan ervan uit dat we de volgende gegevens hebben vastgehouden om onze diabetesclassificatie te valideren:
| Bloedglucose (x) | Diabetische? (y) |
|---|---|
| 66 | 0 |
| 107 | 1 |
| 112 | 1 |
| 71 | 0 |
| 87 | 1 |
| 89 | 1 |
Het toepassen van de logistieke functie die we eerder hebben afgeleid op de x-waarden , resulteert in de volgende plot.
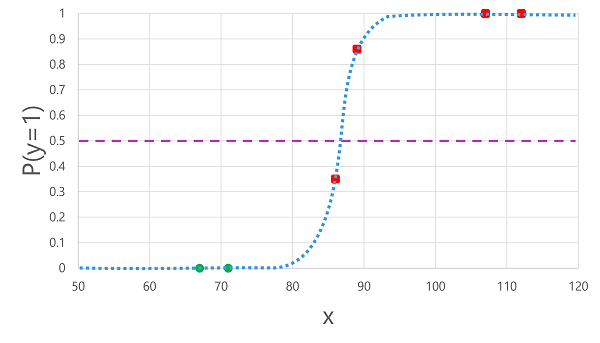
Op basis van of de waarschijnlijkheid die door de functie wordt berekend boven of onder de drempelwaarde ligt, genereert het model een voorspeld label van 1 of 0 voor elke observatie. Vervolgens kunnen we de voorspelde klasselabels (ŷ) vergelijken met de werkelijke klasselabels (y), zoals hier wordt weergegeven:
| Bloedglucose (x) | Werkelijke diabetesdiagnose (y) | Voorspelde diabetesdiagnose (ŷ) |
|---|---|---|
| 66 | 0 | 0 |
| 107 | 1 | 1 |
| 112 | 1 | 1 |
| 71 | 0 | 0 |
| 87 | 1 | 0 |
| 89 | 1 | 1 |
Metrische gegevens voor evaluatie van binaire classificatie
De eerste stap bij het berekenen van metrische evaluatiegegevens voor een binair classificatiemodel is meestal het maken van een matrix van het aantal juiste en onjuiste voorspellingen voor elk mogelijk klasselabel:
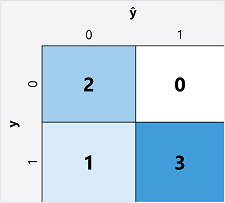
Deze visualisatie wordt een verwarringsmatrix genoemd en toont de voorspellingstotalen waarbij:
- ŷ=0 en y=0: Terecht negatieven (TN)
- ŷ=1 en y=0: Fout-positieven (FP)
- ŷ=0 en y=1: Fout-negatieven (FN)
- ŷ=1 en y=1: Terecht positieven (TP)
De rangschikking van de verwarringsmatrix is zodanig dat juiste (true) voorspellingen worden weergegeven in een diagonale lijn van linksboven naar rechtsonder. Vaak wordt kleurintensiteit gebruikt om het aantal voorspellingen in elke cel aan te geven, dus een snelle blik op een model dat goed voorspelt, zou een diep gearceerde diagonale trend moeten onthullen.
Nauwkeurigheid
De eenvoudigste meetwaarde die u kunt berekenen op basis van de verwarringsmatrix is nauwkeurigheid : het aandeel voorspellingen dat het model juist heeft gekregen. Nauwkeurigheid wordt berekend als:
(TN+TP) ÷ (TN+FN+FP+TP)
In het geval van ons diabetesvoorbeeld is de berekening:
(2+3) ÷ (2+1+0+3)
= 5 ÷ 6
= 0.83
Voor onze validatiegegevens leverde het diabetesclassificatiemodel dus 83% van de tijd de juiste voorspellingen op.
Nauwkeurigheid lijkt in eerste instantie een goede metriek om een model te evalueren, maar overweeg dit. Stel dat 11% van de populatie diabetes heeft. U kunt een model maken dat altijd 0 voorspelt en het zou een nauwkeurigheid van 89% bereiken, zelfs als het geen echte poging doet om onderscheid te maken tussen patiënten door hun functies te evalueren. Wat we echt nodig hebben, is een dieper inzicht in hoe het model presteert bij het voorspellen van 1 voor positieve gevallen en 0 voor negatieve gevallen.
Intrekken
Relevante overeenkomsten is een metrische waarde die het aandeel positieve gevallen meet dat het model correct heeft geïdentificeerd. Met andere woorden, vergeleken met het aantal patiënten met diabetes, hoeveel voorspelde het model om diabetes te hebben?
De formule voor intrekken is:
TP ÷ (TP+FN)
Voor ons diabetesvoorbeeld:
3 ÷ (3+1)
= 3 ÷ 4
= 0.75
Ons model identificeerde dus 75% van de patiënten die diabetes hebben als diabetes.
Precisie
Precisie is vergelijkbaar met de relevante metrische gegevens, maar meet het aandeel van voorspelde positieve gevallen waarbij het werkelijke label daadwerkelijk positief is. Met andere woorden, welk aandeel van de patiënten voorspeld door het model om diabetes daadwerkelijk te hebben?
De formule voor precisie is:
TP-÷ (TP+FP)
Voor ons diabetesvoorbeeld:
3 ÷ (3+0)
= 3 ÷ 3
= 1.0
Dus 100% van de patiënten die door ons model zijn voorspeld om diabetes te hebben, hebben in feite diabetes.
F1-score
F1-score is een algemene metriek die gecombineerde relevante overeenkomsten en precisie combineert. De formule voor F1-score is:
(2 x Precision x Recall) ÷ (Precision + Recall)
Voor ons diabetesvoorbeeld:
(2 x 1,0 x 0,75) ÷ (1,0 + 0,75)
= 1,5 ÷ 1,75
= 0,86
Gebied onder de curve (AUC)
Een andere naam voor relevante overeenkomsten is de werkelijke positieve rente (TPR) en er is een equivalente metriek genaamd de fout-positieve frequentie (FPR) die wordt berekend als FP÷(FP+TN). We weten al dat de TPR voor ons model bij het gebruik van een drempelwaarde van 0,5 0,75 is en dat we de formule voor FPR kunnen gebruiken om een waarde van 0÷2 = 0 te berekenen.
Als we natuurlijk de drempelwaarde zouden wijzigen waar (1), zou dit van invloed zijn op het aantal positieve en negatieve voorspellingen; en dus de metrische gegevens TPR en FPR wijzigen. Deze metrische gegevens worden vaak gebruikt om een model te evalueren door een ontvangen ROC-curve (Operator Characteristic ) uit te tekenen waarmee de TPR en FPR worden vergeleken voor elke mogelijke drempelwaarde tussen 0,0 en 1.0:
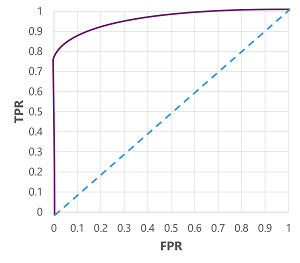
De ROC-curve voor een perfect model zou de TPR-as aan de linkerkant recht omhoog gaan en vervolgens over de FPR-as aan de bovenkant. Omdat het tekengebied voor de curve 1x1 meet, is het gebied onder deze perfecte curve 1,0 (wat betekent dat het model 100% van de tijd juist is). Daarentegen vertegenwoordigt een diagonale lijn van linksonder naar rechtsboven de resultaten die worden bereikt door willekeurig een binair label te raden; het produceren van een gebied onder de curve van 0,5. Met andere woorden, gezien twee mogelijke klasselabels, kunt u redelijkerwijs verwachten dat 50% van de tijd correct wordt geraden.
In het geval van ons diabetesmodel wordt de bovenstaande curve geproduceerd en is het gebied onder de curve (AUC) 0,875. Omdat de AUC hoger is dan 0,5, kunnen we concluderen dat het model beter presteert bij het voorspellen of een patiënt diabetes heeft dan willekeurig raden.