Regressie
Regressiemodellen worden getraind om numerieke labelwaarden te voorspellen op basis van trainingsgegevens die zowel functies als bekende labels bevatten. Het proces voor het trainen van een regressiemodel (of inderdaad, een machine learning-model onder supervisie) omvat meerdere iteraties waarin u een geschikt algoritme (meestal met een aantal geparameteriseerde instellingen) gebruikt om een model te trainen, de voorspellende prestaties van het model te evalueren en het model te verfijnen door het trainingsproces met verschillende algoritmen en parameters te herhalen totdat u een acceptabel nauwkeurigheidsniveau hebt bereikt.
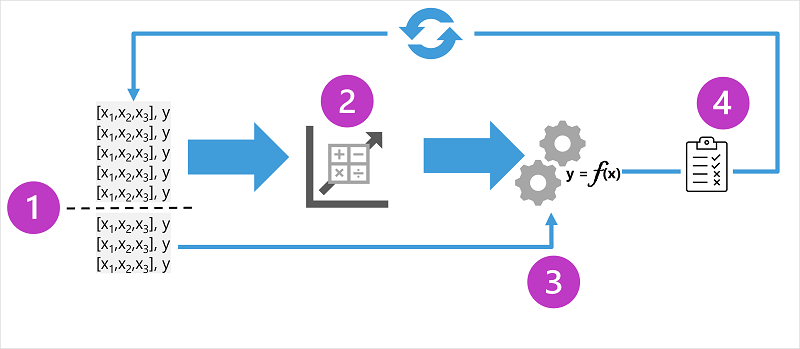
In het diagram ziet u vier belangrijke elementen van het trainingsproces voor machine learning-modellen onder supervisie:
- Splits de trainingsgegevens (willekeurig) om een gegevensset te maken waarmee het model moet worden getraind terwijl u een subset van de gegevens achterhoudt die u gebruikt om het getrainde model te valideren.
- Gebruik een algoritme om de trainingsgegevens aan een model aan te passen. Gebruik in het geval van een regressiemodel een regressie-algoritme zoals lineaire regressie.
- Gebruik de validatiegegevens die u hebt bewaard om het model te testen door labels voor de functies te voorspellen.
- Vergelijk de bekende werkelijke labels in de validatiegegevensset met de labels die door het model zijn voorspeld. Aggregeren vervolgens de verschillen tussen de voorspelde en werkelijke labelwaarden om een metrische waarde te berekenen die aangeeft hoe nauwkeurig het model is voorspeld voor de validatiegegevens.
Na elke training, validatie en evaluatie van iteratie kunt u het proces herhalen met verschillende algoritmen en parameters totdat een acceptabele evaluatiemetriek wordt bereikt.
Voorbeeld: regressie
Laten we regressie verkennen met een vereenvoudigd voorbeeld waarin we een model trainen om een numeriek label (y) te voorspellen op basis van één functiewaarde (x). De meeste echte scenario's hebben betrekking op meerdere functiewaarden, wat enige complexiteit toevoegt; maar het principe is hetzelfde.
Laten we ons bijvoorbeeld houden aan het scenario voor de verkoop van ijsjes dat we eerder hebben besproken. Voor onze functie beschouwen we de temperatuur (laten we aannemen dat de waarde de maximumtemperatuur op een bepaalde dag is) en het label dat we willen trainen om te voorspellen, het aantal ijsjes dat die dag wordt verkocht. We beginnen met enkele historische gegevens met records van dagelijkse temperaturen (x) en ijsverkoop (y):
 |
 |
|---|---|
| Temperatuur (x) | Verkoop van ijsjes (y) |
| 51 | 1 |
| 52 | 0 |
| 67 | 14 |
| 65 | 14 |
| 70 | 23 |
| 69 | 20 |
| 72 | 23 |
| 75 | 26 |
| 73 | 22 |
| 81 | 30 |
| 78 | 26 |
| 83 | 36 |
Een regressiemodel trainen
We beginnen met het splitsen van de gegevens en het gebruik van een subset ervan om een model te trainen. Dit is de trainingsgegevensset:
| Temperatuur (x) | Verkoop van ijsjes (y) |
|---|---|
| 51 | 1 |
| 65 | 14 |
| 69 | 20 |
| 72 | 23 |
| 75 | 26 |
| 81 | 30 |
Om inzicht te krijgen in hoe deze x - en y-waarden zich met elkaar kunnen verhouden, kunnen we ze als coördinaten op twee assen uitzetten, zoals deze:
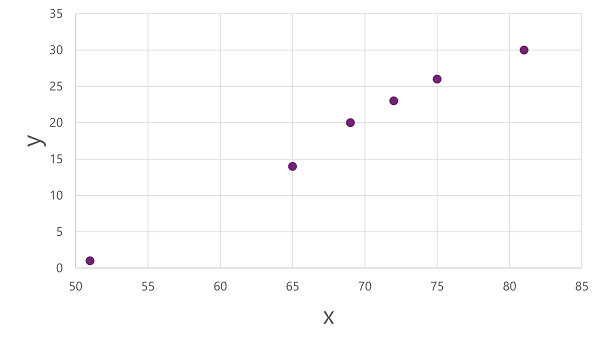
Nu zijn we klaar om een algoritme toe te passen op onze trainingsgegevens en deze aan te passen aan een functie die een bewerking toepast op x om y te berekenen. Een dergelijk algoritme is lineaire regressie, die werkt door een functie af te leiden die een rechte lijn produceert door de snijpunten van de x- en y-waarden, terwijl de gemiddelde afstand tussen de lijn en de getekende punten wordt geminimaliseerd, zoals hier:
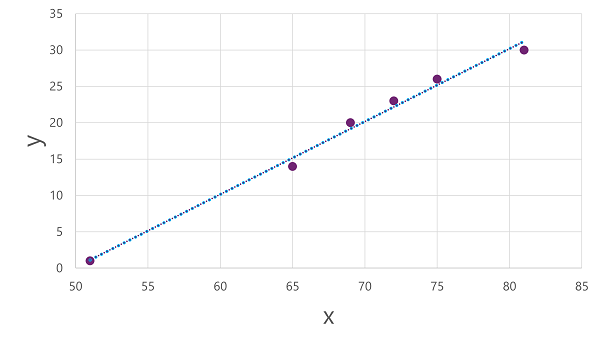
De lijn is een visuele weergave van de functie waarin de helling van de lijn beschrijft hoe u de waarde van y voor een bepaalde waarde van x berekent. De lijn onderschept de x-as op 50, dus als x 50 is, is y 0. Zoals u kunt zien vanuit de asmarkeringen in het diagram, loopt de lijn af, zodat elke toename van 5 langs de x-as resulteert in een toename van 5 op de y-as, dus wanneer x 55 is, y 5 is; wanneer x 60 is, y 10, enzovoort. Als u een waarde van y wilt berekenen voor een bepaalde waarde van x, trekt de functie gewoon 50 af; met andere woorden, de functie kan als volgt worden uitgedrukt:
f(x) = x-50
U kunt deze functie gebruiken om het aantal verkochte ijsjes op een dag met een bepaalde temperatuur te voorspellen. Stel dat de weersvoorspelling ons vertelt dat het morgen 77 graden is. We kunnen ons model toepassen om 77-50 te berekenen en te voorspellen dat we morgen 27 ijsjes verkopen.
Maar hoe nauwkeurig is ons model?
Een regressiemodel evalueren
Om het model te valideren en te evalueren hoe goed het voorspelt, hebben we enkele gegevens vastgehouden waarvoor we de labelwaarde (y) kennen. Dit zijn de gegevens die we hebben bewaard:
| Temperatuur (x) | Verkoop van ijsjes (y) |
|---|---|
| 52 | 0 |
| 67 | 14 |
| 70 | 23 |
| 73 | 22 |
| 78 | 26 |
| 83 | 36 |
We kunnen het model gebruiken om het label voor elk van de waarnemingen in deze gegevensset te voorspellen op basis van de functiewaarde (x) en vervolgens het voorspelde label (ŷ) te vergelijken met de bekende werkelijke labelwaarde (y).
Het model dat we eerder hebben getraind, waarmee de functie f(x) = x-50 wordt ingekapseld, resulteert in de volgende voorspellingen:
| Temperatuur (x) | Werkelijke verkoop (y) | Voorspelde verkoop (ŷ) |
|---|---|---|
| 52 | 0 | 2 |
| 67 | 14 | 17 |
| 70 | 23 | 20 |
| 73 | 22 | 23 |
| 78 | 26 | 28 |
| 83 | 36 | 33 |
We kunnen zowel de voorspelde als de werkelijke labels uitzetten op basis van de functiewaarden als volgt:
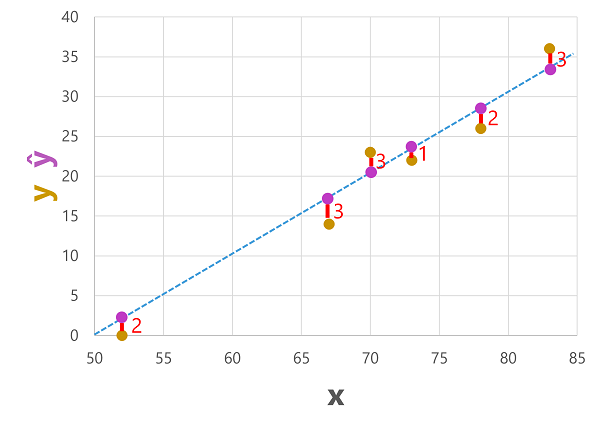
De voorspelde labels worden berekend door het model, zodat ze zich op de functielijn bevinden, maar er is een variantie tussen de ŷ waarden die door de functie worden berekend en de werkelijke y-waarden uit de validatiegegevensset. Dit wordt in het diagram aangegeven als een lijn tussen de ŷ- en y-waarden die aangeven hoe ver van de voorspelling de werkelijke waarde was.
Metrische regressieevaluatiegegevens
Op basis van de verschillen tussen de voorspelde en werkelijke waarden kunt u enkele algemene metrische gegevens berekenen die worden gebruikt om een regressiemodel te evalueren.
Gemiddelde absolute fout (MAE)
De variantie in dit voorbeeld geeft aan hoeveel ijsjes elke voorspelling onjuist was. Het maakt niet uit of de voorspelling is overschreden of onder de werkelijke waarde (bijvoorbeeld -3 en +3 geven beide een variantie van 3 aan). Deze metrische waarde staat bekend als de absolute fout voor elke voorspelling en kan worden samengevat voor de hele validatieset als de gemiddelde absolute fout (MAE).
In het ijsvoorbeeld is het gemiddelde (gemiddelde) van de absolute fouten (2, 3, 3, 1, 2 en 3) 2,33.
Gemiddelde kwadratische fout (MSE)
De gemiddelde absolute foutmetrie neemt alle verschillen tussen voorspelde en werkelijke labels in gelijke mate in aanmerking. Het kan echter wenselijker zijn om een model te hebben dat consistent verkeerd is met een kleine hoeveelheid dan een model dat minder, maar grotere fouten maakt. Eén manier om een metrische waarde te produceren die grotere fouten 'amplifieert' door de afzonderlijke fouten te kwadrateren en het gemiddelde van de kwadratische waarden te berekenen. Deze metrische waarde wordt de gemiddelde kwadratische fout (MSE) genoemd.
In ons ijsvoorbeeld is het gemiddelde van de kwadratische absolute waarden (4, 9, 9, 1, 4 en 9) 6.
Wortel van gemiddelde kwadratische fout (RMSE)
De gemiddelde kwadratische fout helpt rekening te houden met de grootte van fouten, maar omdat deze de foutwaarden kwadrat, vertegenwoordigt de resulterende metrische waarde niet langer de hoeveelheid die door het label wordt gemeten. Met andere woorden, we kunnen zeggen dat de MSE van ons model 6 is, maar dat meet niet de nauwkeurigheid in termen van het aantal ijsjes dat verkeerd is aangegeven; 6 is slechts een numerieke score die het foutniveau in de validatievoorspellingen aangeeft.
Als we de fout willen meten in termen van het aantal ijsjes, moeten we de vierkantswortel van de MSE berekenen. Dit resulteert in een metrische waarde die niet verwonderlijk wordt aangeroepen, Wortel gemiddelde kwadratische fout. In dit geval √6, dat is 2,45 (ijsjes).
Bepalingscoëfficiënt (R2)
Alle metrische gegevens tot nu toe vergelijken de discrepantie tussen de voorspelde en werkelijke waarden om het model te evalueren. In werkelijkheid is er echter een natuurlijke willekeurige variantie in de dagelijkse verkoop van ijs waarmee het model rekening houdt. In een lineair regressiemodel past het trainingsalgoritmen op een rechte lijn die de gemiddelde variantie tussen de functie en de bekende labelwaarden minimaliseert. De bepalingscoëfficiënt (meestal R 2 of R-Squared genoemd) is een metrische waarde die het aandeel van variantie meet in de validatieresultaten die door het model kunnen worden verklaard, in plaats van een afwijkend aspect van de validatiegegevens (bijvoorbeeld een dag met een zeer ongebruikelijk aantal ijsverkoop vanwege een lokaal festival).
De berekening voor R2 is complexer dan voor de vorige metrische gegevens. Het vergelijkt de som van kwadratische verschillen tussen voorspelde en werkelijke labels met de som van kwadratische verschillen tussen de werkelijke labelwaarden en het gemiddelde van werkelijke labelwaarden, zoals:
R2 = 1- ∑(y-ŷ)2 ÷ ∑(y-ȳ)2
Maak je geen zorgen als dat ingewikkeld lijkt; De meeste machine learning-hulpprogramma's kunnen de metrische gegevens voor u berekenen. Het belangrijkste punt is dat het resultaat een waarde is tussen 0 en 1 die het aandeel van de variantie beschrijft die door het model wordt uitgelegd. Hoe dichter bij 1 deze waarde ligt, hoe beter het model de validatiegegevens past. In het geval van het regressiemodel voor ijs is de R2 berekend op basis van de validatiegegevens 0,95.
Iteratieve training
De hierboven beschreven metrische gegevens worden vaak gebruikt om een regressiemodel te evalueren. In de meeste praktijkscenario's gebruikt een data scientist een iteratief proces om een model herhaaldelijk te trainen en evalueren, variërend:
- Functieselectie en -voorbereiding (kiezen welke functies u wilt opnemen in het model en berekeningen die erop worden toegepast om ervoor te zorgen dat deze beter passen).
- Algoritmeselectie (We hebben lineaire regressie in het vorige voorbeeld verkend, maar er zijn veel andere regressiealgoritmen)
- Algoritmeparameters (numerieke instellingen om het gedrag van algoritmen te beheren, nauwkeuriger hyperparameters genoemd om deze te onderscheiden van de x- en y-parameters).
Na meerdere iteraties wordt het model dat resulteert in de beste evaluatiemetriek die acceptabel is voor het specifieke scenario geselecteerd.