Wat is superpositie in kwantumcomputing?
Als de kat uit de vorige eenheid een kwantumkat was, zou de toestand van de kwantumkat en het doossysteem hetzelfde zijn: de som van de zes verschillende posities van de kwantumkat met betrekking tot het vak, gewogen door de waarschijnlijkheid van het vinden van de kwantum kat in die positie. Het enige verschil is dat de klassieke kat zich in één (en slechts één) van zes mogelijke posities kan bevinden, terwijl de kwantumkat zich in alle zes posities tegelijk kan bevinden!
In de klassieke wereld kunnen objecten zich slechts in één staat tegelijk bevinden. In de kwantumwereld kunnen kwantumdeeltjes zich echter in meerdere toestanden tegelijk bevinden. Dit fenomeen wordt superpositie genoemd.
In kwantumcomputing gebruikt niemand kwantumkatten , helaas - maar qubits. Het woord 'qubit' betekent 'kwantumbit'. Net als bij klassieke computing, waarbij de basiseenheid van informatie de bit is, is de basiseenheid van informatie in kwantumcomputing de qubit. En net als de bit twee mogelijke waarden kan aannemen, 0 en 1, is een qubit elk kwantumdeeltje dat in twee mogelijke toestanden kan zijn. Een qubit kan bijvoorbeeld een foton zijn, die in twee richtingen kan worden gepolariseerd of een elektron, die zich in twee energieniveaus kan bevinden.
Hoe kunt u de superpositie in een qubit vertegenwoordigen? Wat is de kans om een qubit in een bepaalde toestand te vinden?
Hoe kunt u de superpositie in een qubit vertegenwoordigen?
Een qubit is een kwantumdeeltje met twee mogelijke posities of toestanden. Als analoog aan de klassieke bit worden de kwantumtoestanden van een qubit ook wel $0$ en $1$ genoemd. Een qubit kan de status $0$ hebben, in de toestand $1$ en in elke superpositie van beide toestanden. Hoe kunt u deze superpositie vertegenwoordigen?
Stel dat u een cirkel en een verticale en horizontale as tekent, zodat het middelste punt het midden van de cirkel is. De status $0$ wordt op het bovenste punt van de verticale as geplaatst en de toestand $1$ bevindt zich op het onderste punt.
Hoe kunt u deze weergave beschrijven? U kunt zeggen dat de toestand $0$ een pijl is, of een vector, die omhoog wijst en de toestand $1$ een vector is die omlaag wijst. Daarom zou een klassieke bit een vector zijn die omhoog of omlaag wijst, maar nooit in een andere richting.
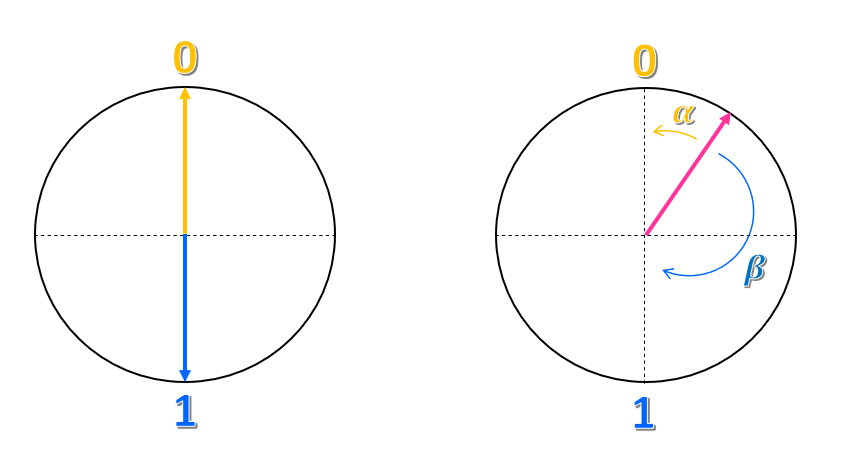
Hoe zit het met een ander punt van de cirkel? Hoe kunt u die status vertegenwoordigen? Net als coördinaten in een vliegtuig, kunt u proberen het te vertegenwoordigen als een combinatie van de twee staten $0$ en $1$. U kunt bijvoorbeeld nemen hoe dicht de vector is van de toestand $0$ en deze hoek $\alpha$ aanroepen, en hoe dichtbij de toestand $1$ is en deze hoek $\beta$ aanroept. We kunnen de status vertegenwoordigen als $\alpha 0 + \beta 1 $. De toestand is dus een superpositie van de staten $0$ en $1$.
Net als bij het voorbeeld van de kat en het vak is de globale toestand van een qubit de som van de afzonderlijke toestanden, $0$ en $1$, gewogen door de waarschijnlijkheid van het vinden van de qubit in die staat, $\alpha$ en $\beta $.

Deze weergave van een qubit is eigenlijk nauwkeurig en wordt ook wel de Bloch-bol genoemd.
Tip
De Bloch sphere is een krachtig hulpmiddel als de bewerkingen die we op een qubit kunnen uitvoeren, kunnen worden weergegeven als rotaties over een van de kardinaliteitsassen. Hoewel het denken over een kwantumberekening als een reeks rotaties een krachtige intuïtieve kennis is, is het lastig om deze intuïtieve methode te gebruiken om algoritmen te ontwerpen en te beschrijven. Q# vermindert dit probleem door een taal op te geven voor het beschrijven van dergelijke rotaties.
Wat is de kans op het vinden van een qubit in een toestand?
Net als in het voorbeeld van de kat en het vak van de vorige eenheid is de globale status van een qubit de som van de afzonderlijke toestanden, $0$ en $1$, gewogen door de waarschijnlijkheid van het vinden van de qubit in die staat, $\alpha$ en $\beta $. De getallen $\alpha$ en $\beta$ geven aan hoe 'close' de qubitstatus is voor respectievelijk $0$ en $1$. Dus, is $\alpha$ en $\beta$ de waarschijnlijkheid van het vinden van de qubit in de toestand $0$ of $1$? Niet precies.
De getallen $\alpha$ en $\beta$ zijn waarschijnlijkheidsamplitudes voor elke status. Hun absolute waarden, bijvoorbeeld $|\alpha|^2$ geven de bijbehorende waarschijnlijkheden. De kans voor het observeren van de toestand $0$ is bijvoorbeeld $|\alpha|^2$, en de kans op het observeren van de toestand $1$ is $|\beta|^2$.
De getallen $\alpha$ en $\beta$ kunnen positieve, negatieve of zelfs complexe getallen zijn. In een geldige kwantumsuperpositie moeten alle waarschijnlijkheden echter worden opgeteld tot één: $|\alpha|^2+|\beta|^2=1$. Deze beperking wordt de normalisatievoorwaarde genoemd. U kunt de normalisatievoorwaarde beschouwen als het feit dat u altijd een resultaat krijgt wanneer u meet, dus de waarschijnlijkheden van het meten van elke mogelijke uitkomst moeten optellen tot één.