Hoe kan ik verstrengeling gebruiken om informatie te verzenden?
In de vorige lessen hebt u geleerd dat kwantumverstrengeling een uitstekende bron voor kwantumcommunicatie kan zijn. In deze les ziet u een van de bekendste toepassingen van verstrengeling: het kwantumteleportatieprotocol.
Bij teleportatie wordt verstrengeling gebruikt om de status van een qubit van de ene locatie naar de andere over te dragen. De status van de qubit wordt overgebracht naar een andere qubit, maar de qubit zelf wordt niet fysiek verplaatst. Dit is belangrijk om te onthouden! De informatie van de status van de qubit wordt overgebracht naar een andere qubit die wordt gebruikt als een vaartuig om de informatie van de bericht-qubit op te schrijven.
Het teleportatieprotocol maakt gebruik van een combinatie van verstrengeling en klassieke communicatie. De klassieke communicatie is belangrijk omdat het teleportatieprotocol vereist dat de afzender de resultaten van de metingen aan de ontvanger communiceert. Dit betekent dat teleportatie geen informatie sneller kan verzenden dan de snelheid van het licht. De klassieke communicatie tussen de afzender en de ontvanger wordt beperkt door de snelheid van het licht.
Laten we het protocol van kwantumteleportatie bekijken.
Het protocol van kwantumteleportatie
Alice en Bob werken samen in hetzelfde bedrijf. Alice is gevestigd in Seattle en Bob is gevestigd in Los Angeles. Ze werken aan een project waarvoor ze kwantuminformatie moeten delen. Ze besluiten kwantumteleportatie te gebruiken om kwantuminformatie ertussen te verzenden.
Eerste configuratie
Alice en Bob hebben elk een qubit die deel uitmaakt van een verstrengeld paar dat eerder is voorbereid. Het verstrengelde paar is een kloktoestand, die de toestand is
$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B} + \ket{1_A 1_B})$$
Alice heeft een extra qubit , de 'message qubit' genoemd, en wil deze qubit naar Bob verzenden. De berichtenqubit heeft een onbekende status die Alice wil teleporteren naar Bob. De status van de berichtenqubit is
$$\ket{m}=\alpha\ket{{0}_m + \beta\ket{{1}_m,$$
waar $\alpha$ en $\beta$ complexe getallen zijn.
De globale status van De drie qubits van Alice en Bob is
$$\ket{\text{Global}}= (\alpha\ket{{0}_m + \beta\ket{1}_m)\otimes\frac 1{\sqrt2}(\ket{0_A 0_B}+ \ket{1_A 1_B})$$
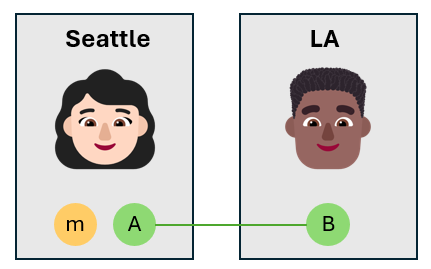
Alice verstrengelt de bericht-qubit met haar eigen qubit
Alice neemt de bericht-qubit en verstrengelt het met haar eigen qubit $A$ met behulp van een CNOT-poort. De bericht-qubit is de controle-qubit en de qubit van Alice is de target qubit. Hiermee wordt een verstrengelde status van drie qubits gemaakt.
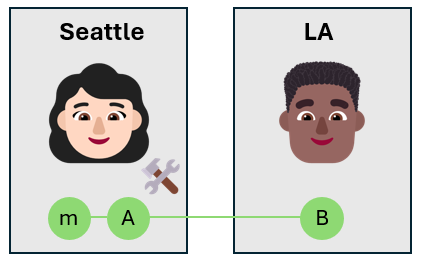
De bericht-qubit heeft de onbekende status $\alpha\ket{0}_m + \beta\ket{1}_m$, dus na het toepassen van de CNOT-poort bevinden de qubits van Alice zich in een superpositie van de vier bellstatussen. De globale status van de drie qubits is
$$ \ket{\text{Global}}=\frac1{{2}\ket{\phi^+}_\text{mA} (\alpha\ket{{0}_B + \beta\ket{{1}_B) +$$
$$+ \frac1{{2}\ket{\phi^-}_\text{mA} (\alpha\ket{0}_B - \beta\ket{1}_B) +$$
$$+ \frac1{{2}\ket{\psi^+}_\text{mA}(\alpha\ket{1}_B + \beta\ket{0}_B) +$$
$$+ \frac1{{2}\ket{\psi^-}_\text{mA} (\alpha\ket{1}_B- \beta\ket{0}_B)$$
De globale status van Alice en Bob's qubits is een superpositie van vier mogelijke toestanden.
Tip
Een goede oefening is om te controleren of de globale status van de drie qubits het bovenstaande is. U kunt dit doen door de CNOT-poort toe te passen op de bericht-qubit en de qubit van Alice en vervolgens de status van de drie qubits uit te breiden.
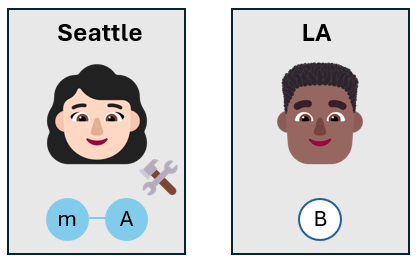
Alice meet de qubits
Alice meet vervolgens de bericht-qubit en haar eigen qubit. Ze meet de qubits in de $Z-basis$ niet zoals gebruikelijk, maar ze kiest de Basis bell. De basis van de klok bestaat uit de vier kloktoestanden, \lbrace $^+\ket{\phi, }^-\ket{\phi, }\ket{\psi^}-\ket{\psi \rbrace}. $
Door de bericht-qubit en haar eigen qubit in de bellbasis te meten, projecteert Alice haar qubits in een van de vier bellstatussen. Omdat de drie qubits verstrengeld zijn, worden de meetresultaten gecorreleerd. Wanneer Alice haar qubits meet, wordt de qubit van Bob ook geprojecteerd in de gecorreleerde status.
Als Alice bijvoorbeeld haar qubits meet en de status $\ket{\phi^-}$bekijkt, wordt de qubit van Bob geprojecteerd in de status $\alpha\ket{0}_B - \beta\ket{1}_B$.
Alice roept Bob aan
Alice noemt Bob en vertelt hem de resultaten van haar metingen. Ze gebruikt een klassiek communicatiekanaal, zoals een telefoongesprek of een sms-bericht.
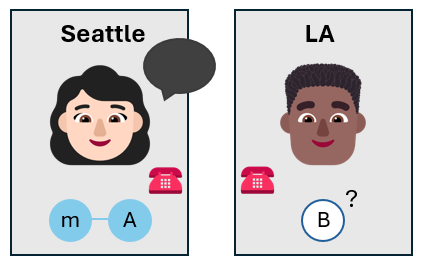
Bob kent nu de status van zijn eigen qubit, zonder dat hij het hoeft te meten. De status van de qubit van Bob is mogelijk niet hetzelfde als de status van de bericht-qubit die Alice wilde teleporteren, maar het is dicht bij de qubit.
Bob past een kwantumbewerking toe
Vervolgens kan Bob de oorspronkelijke status van de bericht-qubit herstellen door een specifieke kwantumbewerking toe te passen op zijn qubit. De operatie die Bob uitvoert, is afhankelijk van wat Alice hem telefonisch vertelde.
De operatie die hij uitvoert, kan een Pauli X-poort$, een Pauli $$Z-poort$, beide of geen zijn.
Als het resultaat van de meting van Alice bijvoorbeeld ^-is, weet Bob dat zijn qubit de status $\ket{\phiheeft (}$$_B -\alpha\ket{0} _B)\beta.\ket{1}$ Hij hoeft alleen een Pauli Z-poort toe te passen om de oorspronkelijke staat van de bericht qubit te herstellen.
| Metingen van Alice | Bob is van toepassing |
|---|---|
| $\ket{\phi^+}$ | Geen bewerking |
| $\ket{\phi^-}$ | Pauli Z gate |
| $\ket{\psi^+}$ | Pauli X-poort |
| $\ket{\psi^-}$ | Pauli X gate gevolgd door Pauli Z gate |
Met deze laatste bewerking wordt de status van de bericht-qubit effectief teleporteert naar de qubit van Bob. Missie volbracht!
Belangrijk
Het toepassen van een bewerking op een qubit is niet hetzelfde als het meten ervan. Wanneer Bob de bewerking toepast, meet hij zijn qubit niet. Hij past een kwantumbewerking toe waarmee de status van de qubit wordt gewijzigd, maar niet wordt samengevouwen.
In de volgende les implementeert u het kwantumteleportatieprotocol in een Q#-programma.