Oefening: kwantumverstrengeling maken met Q#

7 minuten

In de vorige les hebt u geleerd over het concept van kwantumverstrengeling en bellstatussen.

Nu gaan we kwantumverstrengeling maken met behulp van Q# en de Azure Quantum Development Kit. Als u verstrengeling wilt maken, moet u twee kwantumbewerkingen toepassen: de Hadamard-bewerking en de bewerking Controlled-NOT (CNOT).

Laten we eerst begrijpen hoe deze bewerkingen werken en hoe ze verstrengeling creëren.

De bewerking Controlled-NOT (CNOT)

Wanneer twee qubits zijn verstrengeld, is de status van één qubit afhankelijk van de toestand van de andere qubit. Om twee qubits te verstrengelen, hebt u daarom een bewerking nodig die op beide qubits tegelijk werkt. Dit wordt een multiqubit-bewerking genoemd.

Als u kwantumverstrengeling wilt maken, hebt u de multiqubit-bewerking CNOT nodig, die staat voor Controlled-NOT. Deze bewerking neemt twee qubits als invoer, één fungeert als controle-qubit en de andere is de target qubit. De CNOT bewerking spiegelt de status van de tweede qubit (de target qubit) als en alleen als de status van de eerste qubit (de controle-qubit) 1$| is\rangle$.

Invoer	Uitvoer
$\ket{00}$	$\ket{00}$
$\ket{01}$	$\ket{01}$
$\ket{10}$	$\ket{11}$
$\ket{11}$	$\ket{10}$

In Q#, de CNOT bewerking werkt op een matrix van twee qubits, en het spiegelt de tweede qubit als de eerste qubit is One.

Verstrengeling met Hadamard- en CNOT-bewerkingen

Door de Hadamard$

Dit werkt als volgt:

Neem twee qubits in de status $|00\rangle$. De eerste qubit is de controle-qubit en de tweede qubit is de target qubit.
Maak alleen een superpositiestatus in de controle-qubit door H$ toe te passen$.

$$H |0_c\rangle=\frac{1}{\sqrt{{2}}(|0_c\rangle+|1_c)\rangle$$

Tip

De subscripts ${}_c$ en ${}_t$ het besturingselement en target de qubits opgeven.
Pas de $CNOT-operator$ toe op de controle-qubit, die zich in een superpositiestatus bevindt en de target qubit, die zich in de status $|0_t\rangle$ bevindt.

$$CNOT (\frac{1}{\sqrt{2}}0_c\ket{+}1_c\ket{)}_t \ket{0} CNOT =\frac{1}{\sqrt2}(\ket{0_c 0_t}+|\ket{1_c 0_t})=$$$$=\frac{{1}{\sqrt2}(CNOT \ket{0_c 0_t} + CNOT \ket{1_c 0_t})=$$$$=\frac{1}{\sqrt2}(\ket{0_c 0_t}+\ket{1_c 1_t)}$$

Kwantumverstrengeling maken in Q#

U begint met het maken van een nieuw Q#-bestand in Visual Studio Code.

Open Visual Studio Code.
Selecteer Nieuw > tekstbestand bestand en sla het op als Main.qs.
Selecteer Weergave -> Opdrachtpalet en typQ#: Stel het Azure Quantum QIR-profiel target in. Druk op Enter.
Selecteer Q#: Onbeperkt.

De belstatus $\ket{\phi^+ maken}$

Laten we beginnen met het maken van de belstatus $\ket{\phi^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$.

Eerst moet u de Microsoft.Quantum.Diagnostics naamruimte importeren uit de Standard-bibliotheek, die de DumpMachine functie bevat. Deze functie toont de huidige status van de qubits. Kopieer en plak de volgende Q# code in het bestand Main.qs .
```
import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
```
Tip

U kunt ook de Standaardbibliotheek importeren door deze Microsoft.Quantum te vervangen door Std. import Std.Diagnostics.* is bijvoorbeeld gelijk aan import Microsoft.Quantum.Diagnostics.*.

Maak de Main bewerking die twee Result typewaarden retourneert. Dit zijn de meetresultaten van de qubits.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    // Your code goes here
}

Binnen de Main bewerking wijst u twee qubits toe en q1, die verstrengeld q2 worden.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());
}

Pas de Hadamard-poort, Hop de eerste qubit, q1toe om deze in een superpositiestatus te plaatsen. Verstrengel vervolgens de twee qubits met behulp van de CNOT bewerking.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);
}

Gebruik de DumpMachine functie om de huidige status van de qubits weer te geven. Dit is niet hetzelfde als het meten van de qubits.

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);

    DumpMachine();
}

Meet de qubits met behulp van de M bewerking en sla de resultaten op in m1 en m2. Gebruik vervolgens de Reset bewerking om de qubits opnieuw in te stellen. In Q#moet u de qubits altijd opnieuw instellen op de $|status 0\rangle$ .

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {

    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);
    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

}

Retourneer ten slotte de meetresultaten van de qubits met de return instructie. Het bestand Main.qs moet er als volgt uitzien:

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);

    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

    return (m1, m2);
}

Als u uw programma wilt uitvoeren op de ingebouwde simulator, klikt u op Uitvoeren boven de bewerking of drukt u op Main. Uw uitvoer wordt weergegeven in de console voor foutopsporing.
De meetresultaten worden gecorreleerd, dus aan het einde van het programma krijgt u een resultaat van (Zero, Zero) of (One, One) met gelijke waarschijnlijkheid.
U kunt het circuitdiagram visualiseren door te klikken op Circuit in de lijst met opdrachten boven de Main bewerking. In het circuitdiagram ziet u dat de Hadamard-poort is toegepast op de eerste qubit en de CNOT-poort die op beide qubits is toegepast.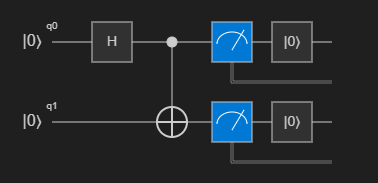

Hoe maak je andere Bell states

Als u andere Bell-statussen wilt maken, moet u extra Pauli $X$ - en $Z-bewerkingen$ toepassen op de qubits.

Als u bijvoorbeeld de klokstatus $\ket{\phi^-}=\frac1{\sqrt2}(|00-11\rangle|)\rangle wilt maken, kunt u de Bewerking Pauli $Z$ toepassen op de controle-qubit nadat u de Hadamard-poort$ hebt toegepast. Met $de Z-bewerking$ wordt de status $\ket{+}$ omgedraaid naar $\ket{-}$.

Tip

De toestanden $\frac{{1}{\sqrt{2}}(|0\rangle+|1\rangle)$ en $\frac{1}{\sqrt{{2}}(|0\rangle -|1\rangle)$ worden ook wel $\ket{+}$ en $\ket{{-}$respectievelijk genoemd.

Dit werkt als volgt:

Neem twee qubits in de status $|00\rangle$.
Maak alleen een superpositiestatus in de controle-qubit door H$ toe te passen$.

$$H |0_c\rangle=\frac{{1}{\sqrt{2}}(|0_c\rangle+|1_c\rangle) =\ket{+_c}$$
Pas de $Z-bewerking$ toe op de controle-qubit.

$$Z \frac{{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)=\frac{1}{\sqrt{{2}}(|0_c-1_c\rangle|)\rangle=\ket{-_c{-}$$
Pas de $CNOT-operator$ toe op de controle-qubit en de target qubit, die de status $|0_t\rangle$ heeft.

$$CNOT (\frac{1}{\sqrt{2}}0_c-1_c\ket{}\ket{)}_t \ket{0} CNOT =\frac{1}{\sqrt2}(\ket{0_c 0_t-1_c 0_t}|\ket{})=$$$$=\frac{{1}{\sqrt2}(CNOT 0_c 0_t\ket{ - CNOT }\ket{1_c 0_t})=$$$$=\frac{1}{\sqrt2}(\ket{0_c 0_t-1_c 1_t)}\ket{}$$

Op dezelfde manier kunnen bellstatussen $\ket{\psi^+}$ en $\ket{\psi^- worden gemaakt door de Pauli }$X$-$ en $Z-bewerkingen$ toe te passen op de qubits.

De klokstatus $\ket{\psi^+}=\frac1{\sqrt2}(|01\rangle+|10\rangle)$ kan worden gemaakt door de Pauli $X-bewerking$ toe te passen op de target qubit nadat de Hadamard-poort is toegepast.
De klokstatus $\ket{\psi^-}=\frac1{\sqrt2}(|01-10\rangle|\rangle)$ kan worden gemaakt door de Pauli $Z$ toe te passen op de controle-qubit en de Pauli $X$ op de target qubit na het toepassen van de Hadamard-poort.

De belstatus $\ket{\phi^-}$ maken in Q#

Wijzig de Q# code om de klokstatus $\ket{\phi^-}$te maken. Het bestand Main.qs moet er als volgt uitzien:

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    Z(q1); // Apply the Pauli Z operation to the control qubit
    CNOT(q1, q2);

    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

    return (m1, m2);
}

Als u uw programma wilt uitvoeren op de ingebouwde simulator, klikt u op Uitvoeren boven de bewerking of drukt u op Main. Uw uitvoer wordt weergegeven in de console voor foutopsporing.
U kunt het circuitdiagram visualiseren door te klikken op Circuit in de lijst met opdrachten boven de Main bewerking. In het circuitdiagram ziet u dat de Hadamard-poort is toegepast op de eerste qubit, de Pauli $Z-poort$ die is toegepast op de eerste qubit en dat de CNOT-poort is toegepast op beide qubits.

In de volgende les leert u hoe u verstrengeling gebruikt om kwantuminformatie te verzenden, een proces dat kwantumteleportatie wordt genoemd.