Wat is verstrengeling?
Verstrengeling is een van de belangrijkste kenmerken van kwantummechanica die deze onderscheiden van klassieke mechanica. Maar wat is verstrengeling? Hoe werkt het? En waarom is het zo belangrijk voor kwantuminformatie?
In deze les ziet u hoe u kwantumverstrengeling definieert en beschrijft en begrijpt waarom het zo'n krachtige resource is voor kwantumcomputing.
Inzicht in kwantumverstrengeling
Stel dat u twee qubits hebt, $A$ en $B$. De qubits zijn onafhankelijk van elkaar, wat betekent dat de informatie over de toestand van qubit $A$, wat het ook is, alleen behoort tot qubit $A$. Op dezelfde manier behoort de informatie over de status van qubit $B$ tot qubit $B$. U kunt de status van elke qubit beschrijven. In dit geval zijn de qubits niet verstrengeld, omdat ze geen informatie delen.
Stel nu dat u de qubits verstrengelt (u leert hoe u dit later doet). Als qubits A en B verstrengeld $zijn, is de informatie over de toestand van qubit $A$ niet onafhankelijk van de toestand van qubit $B$.$$$ Bij verstrengeling wordt informatie gedeeld tussen beide qubits en is er geen manier om de status van qubit A$ of de toestand van qubit $$B$ af te stellen. U kunt alleen de status van het globale systeem beschrijven, niet de status van de afzonderlijke qubits.
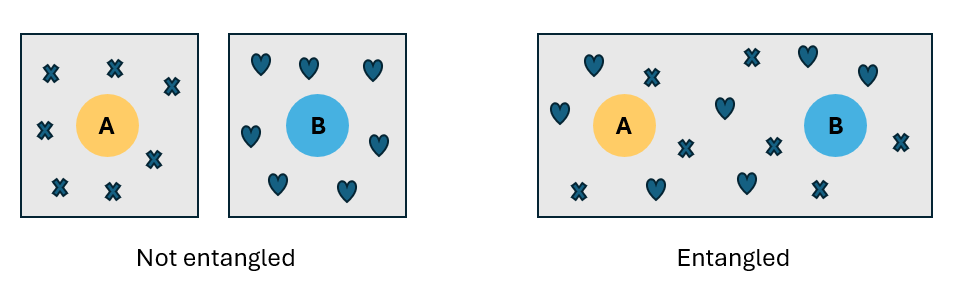
Verstrengeling is een kwantumcorrelatie tussen twee of meer deeltjes. Als twee deeltjes verstrengeld zijn, kunnen ze niet onafhankelijk worden beschreven, maar alleen als een geheel systeem.
Kwantumverstrengeling beschrijven
Stel dat twee qubits $A$ en $B$ zodanig zijn dat de status van het globale systeem $\ket{\phi}$ :
$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B}+ \ket{1_A 1_B})$$
Notitie
In diracatie $\ket{0_A 0_B}=|0\rangle_\text{A}|0\rangle_\text{B}$. De eerste positie komt overeen met de eerste qubit en de tweede positie komt overeen met de tweede qubit.
Het globale systeem $\ket{\phi}$ bevindt zich in een superpositie van de staten $\ket{{00}$ en $\ket{{11}$. Als u beide qubits meet, zijn er slechts twee resultaten mogelijk: $\ket{{00}$ en $\ket{{11}$, en elk heeft dezelfde kans.$\frac{1}{{2}$
Maar wat is de afzonderlijke toestand van qubit $A$? En van qubit $B$? Als u de status van qubit $A$ probeert te beschrijven zonder rekening te houden met de toestand van qubit $B$, mislukt u. Subsystemen A$ en $B$ zijn $, wat betekent dat ze gecorreleerd zijn en niet onafhankelijk kunnen worden beschreven.
Tip
Als u bekend bent met algebra en dirac-notatie, is het een goede oefening om de $\ket{\phi}$ status te wijzigen om iets te krijgen als de toestand van qubit $A$ keer de toestand van qubit $B$. U zult zien dat het onmogelijk is om dit te doen.
De kwantumstatus $\ket{\phi}$ is een speciale verstrengelde toestand, genaamd Klokstatus. Er zijn vier bellstatussen.
$$\ket{\phi^{+}}=\frac1{\sqrt2}\ket{{00} + \frac1{\sqrt2}\ket{{11}$$$$\ket{\phi^{-}}=\frac1{\sqrt2}\ket{00} - \frac1{\sqrt2}\ket{11}$$$$\ket{\psi^{+}}=\frac1{\sqrt2}\ket{{01} + \frac1{\sqrt2}\ket{{10}$$$$\ket{\psi^{-}}=\frac1{\sqrt2}\ket{01} - \frac1 2{\sqrt}\ket{10}$$
Verstrengeling gebruiken als een resource
Op dit moment vraagt u zich misschien af: waarom is verstrengeling zo belangrijk?
Wanneer twee deeltjes zijn verstrengeld, worden subsystemen gecorreleerd en kunnen ze niet onafhankelijk worden beschreven. Maar hier is het interessante deel: de meetresultaten zijn ook gecorreleerd. Dat wil gezegd, wat er ook gebeurt met de toestand van één qubit in een verstrengeld paar, is ook van invloed op de status van de andere qubit.
Denk bijvoorbeeld aan de $\ket{\phistatus ^{+}}$
$$\ket{\phi^{+}}=\frac1{\sqrt2}\ket{{00} + \frac1{\sqrt2}\ket{{11}$$
Als u beide qubits meet, krijgt u $\ket{00}$ of $\ket{11}$ met gelijke waarschijnlijkheid. Er is geen kans op het verkrijgen van de statussen $\ket{01}$ en $\ket{10}$.
Maar wat gebeurt er als u slechts één qubit meet?
Als u alleen de qubit $A-$ meet en u de toestand $\ket{0}$ krijgt, betekent dit dat het globale systeem instort naar de toestand $\ket{00}$. Dit is het enige mogelijke resultaat, omdat de waarschijnlijkheid van het meten van $\ket{01}$ nul is.
Dus zonder de qubit te meten $B$ kunt u positief zijn dat de tweede qubit ook $\ket{0}$ toestand heeft. De meetresultaten worden gecorreleerd omdat de qubits verstrengeld zijn.
Verstrengeling kan bestaan tussen twee deeltjes, zelfs als ze worden gescheiden door grote afstanden. Deze correlatie is sterker dan elke klassieke correlatie en het is een belangrijke resource voor kwantuminformatieverwerkingstaken, zoals kwantumteleportatie, kwantumcryptografie en kwantumcomputing.
In de volgende les schrijft u een Q#-programma waarmee bellstatussen worden gemaakt door kwantumbewerkingen toe te passen op qubits.