Grafieken visualiseren in notitieblokken

10 minuten

Gegevensvisualisatie is een belangrijk aspect van gegevensverkenning. Het omvat het presenteren van gegevens in een grafische indeling, waardoor complexere gegevens begrijpelijker en bruikbaarder worden.

Met Microsoft Fabric-notebooks en Apache Spark-gegevensframes worden uw tabellaire resultaten automatisch weergegeven als grafieken zonder dat hiervoor extra codering nodig is.

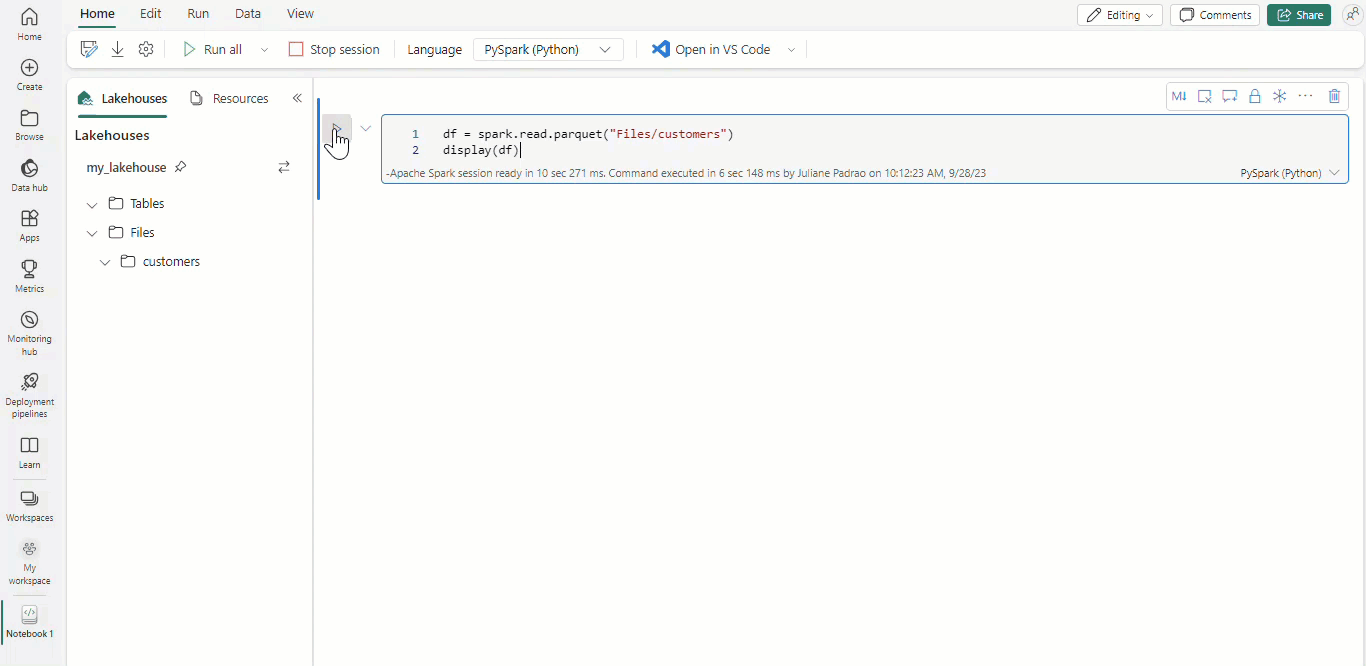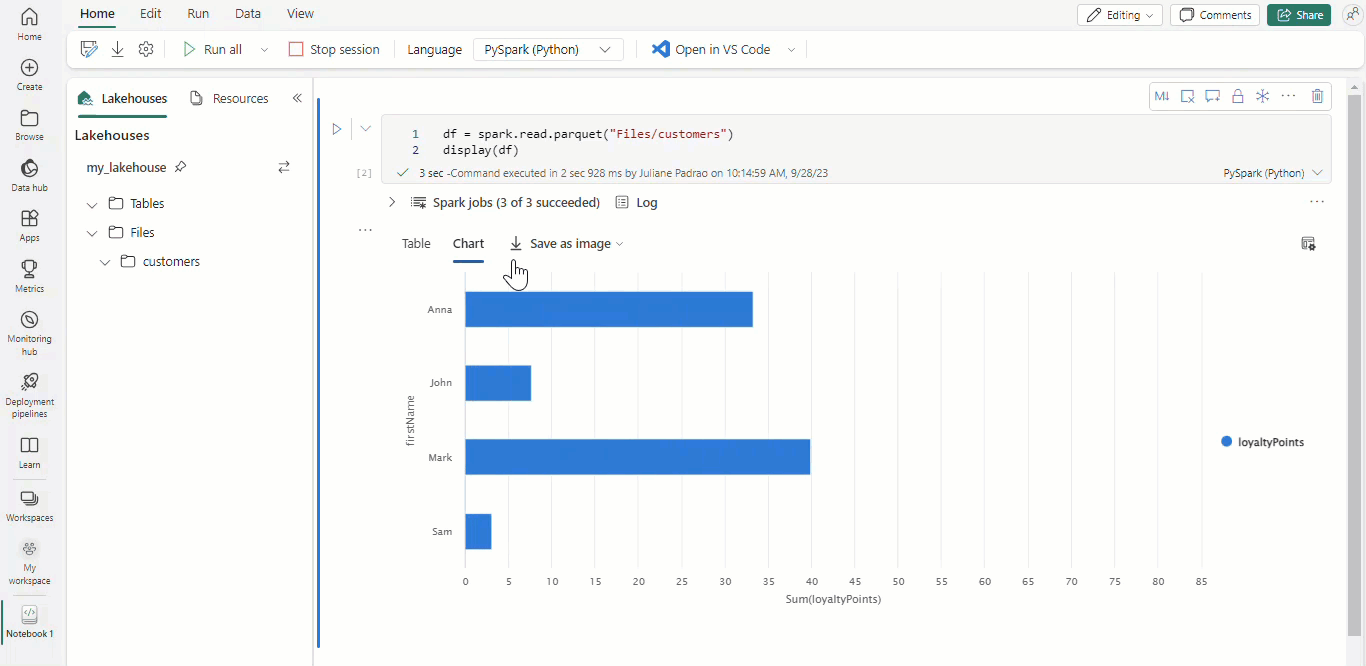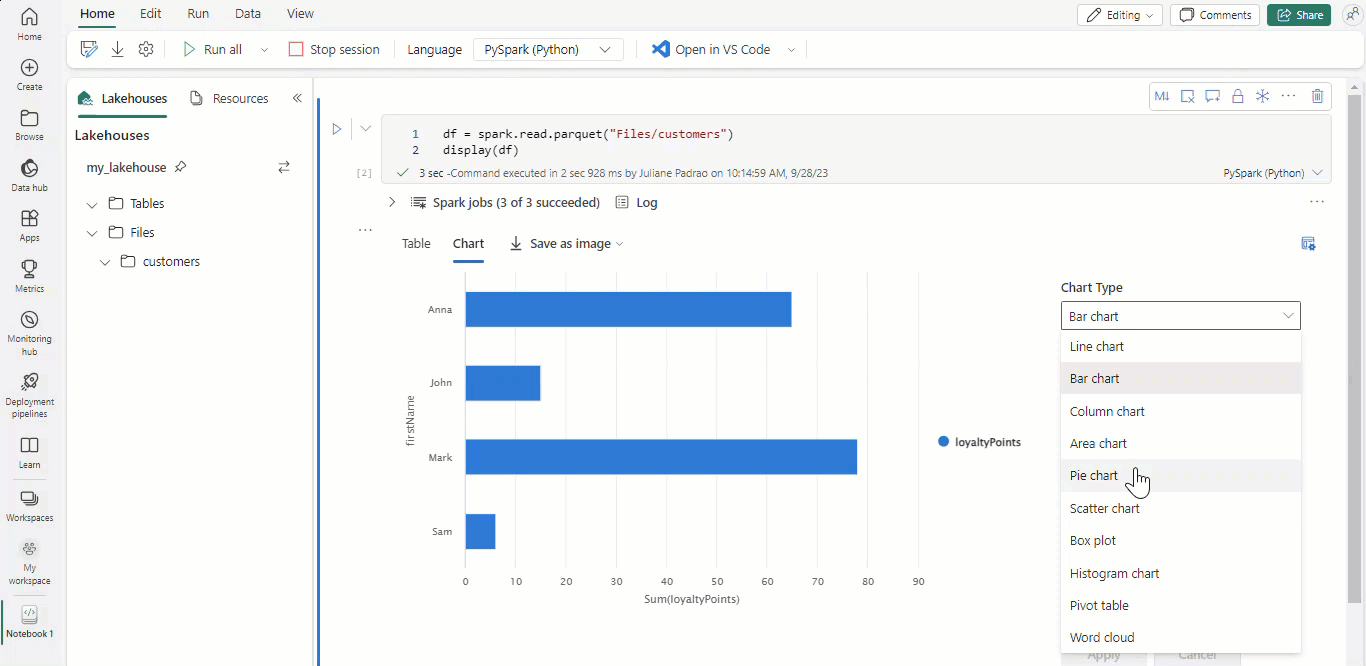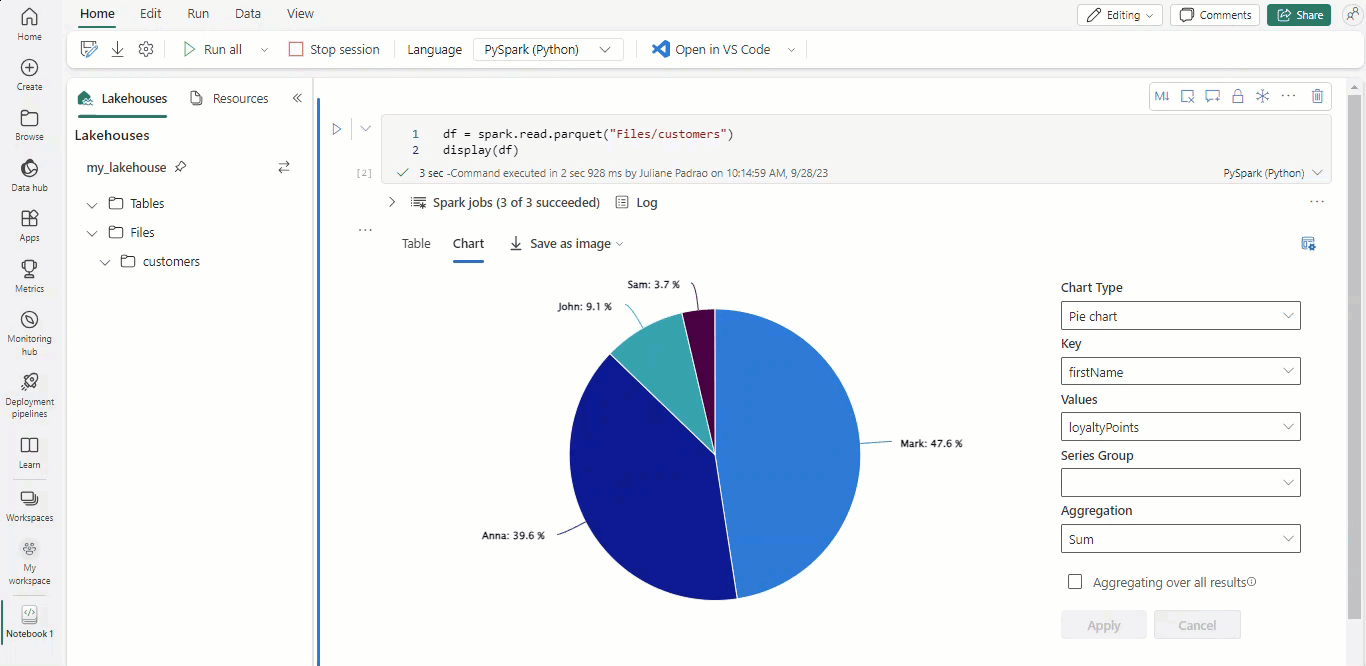
Screenshot of the tabular results being automatically presented as charts without the need for any additional coding.

Tip

Opensource-bibliotheken zoals matplotlib en plotly kunnen ook worden gebruikt om de ervaring voor gegevensverkenning te verbeteren.

Categorische en numerieke variabelen begrijpen

Voor categorische variabelen is het belangrijk om inzicht te hebben in de verschillende categorieën of niveaus in de variabele. Dit omvat het identificeren van het aantal waarnemingen in elke categorie, dat wordt aangeduid als aantallen of frequenties. Daarnaast is het essentieel om te begrijpen welk aandeel of percentage van de waarnemingen elke categorie vertegenwoordigt.

Als het gaat om numerieke variabelen, moeten verschillende aspecten worden overwogen. De centrale tendens van de variabele, die het gemiddelde, de mediaan of de modus kan zijn, geeft een samenvatting van de variabele.

Spreidingsmetingen zoals het bereik, interquartielbereik (IQR), standaarddeviatie of variantie geven inzicht in de verspreiding van de variabele. Ten slotte is het belangrijk om inzicht te krijgen in de verdeling van de variabele. Dit omvat het bepalen of de variabele normaal gesproken wordt gedistribueerd of een andere distributie volgt en eventuele uitbijters identificeert.

Deze worden vaak aangeduid als samenvattingsstatistieken van numerieke en categorische variabelen.

Overzichtsstatistieken

Samenvattingsstatistieken zijn beschikbaar voor Apache Spark-gegevensframes wanneer u de parameter summary=Truegebruikt.

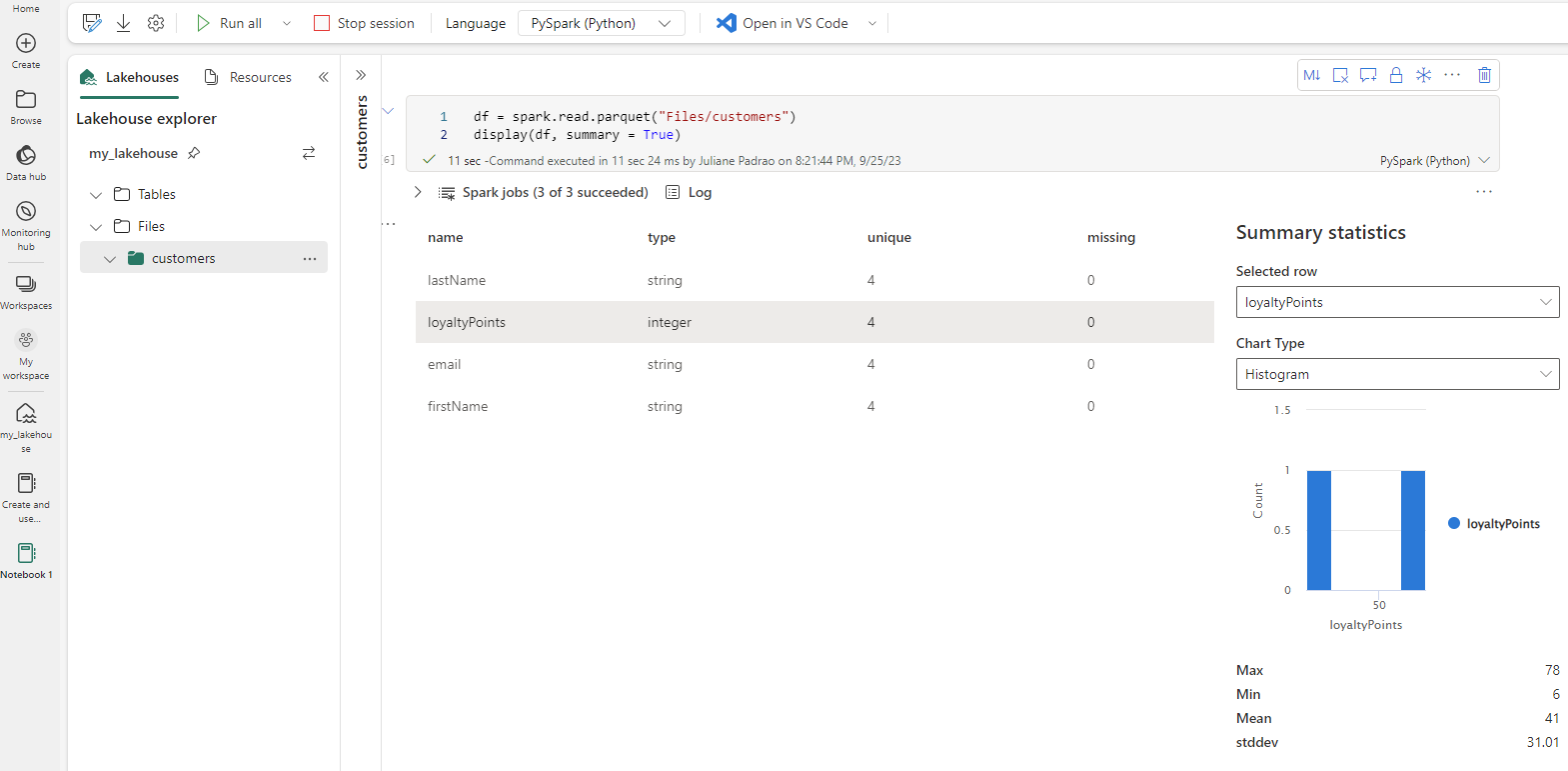
Screenshot of the summary statistics being automatically presented without the need for any additional coding.

U kunt ook de samenvattingsstatistieken genereren met behulp van Python.

import pandas as pd

df = pd.DataFrame({
    'Height_in_cm': [170, 180, 175, 185, 178],
    'Weight_in_kg': [65, 75, 70, 80, 72],
    'Age_in_years': [25, 30, 28, 35, 32]
})

desc_stats = df.describe()
print(desc_stats)

Univariate-analyse

Univariate-analyse is de eenvoudigste vorm van gegevensanalyse waarbij de gegevens die worden geanalyseerd slechts één variabele bevatten. Het belangrijkste doel van een univariate-analyse is het beschrijven van de gegevens en het vinden van patronen die erin bestaan.

Dit zijn veelvoorkomende plots die worden gebruikt om een univariate-analyse uit te voeren.

Histogrammen: wordt gebruikt om de frequentie van elke categorie van een doorlopende variabele weer te geven. Ze kunnen helpen bij het identificeren van de centrale tendens, vorm en verspreiding van de gegevens.
Boxplots: Wordt gebruikt om het bereik, het interkwartielbereik (IQR), de mediaan en potentiële uitbijters van een numerieke variabele weer te geven.
Staafdiagrammen: deze zijn vergelijkbaar met histogrammen, maar worden meestal gebruikt voor categorische variabelen. Elke balk vertegenwoordigt een categorie en de hoogte of lengte van de staaf komt overeen met de frequentie of verhouding ervan.

Met de volgende code maakt u een boxplot en een histogram met behulp van Python.

import numpy as np
import matplotlib.pyplot as plt

# Let's assume these are the heights of a group in inches
heights_in_inches = [63, 64, 66, 67, 68, 69, 71, 72, 73, 55, 75]

fig, axs = plt.subplots(1, 2, figsize=(10, 5))

# Boxplot
axs[0].boxplot(heights_in_inches, whis=0.5)
axs[0].set_title('Box plot of heights')

# Histogram
bins = range(min(heights_in_inches), max(heights_in_inches) + 5, 5)
axs[1].hist(heights_in_inches, bins=bins, alpha=0.5)
axs[1].set_title('Frequency distribution of heights')
axs[1].set_xlabel('Height (in)')
axs[1].set_ylabel('Frequency')

plt.tight_layout()
plt.show()

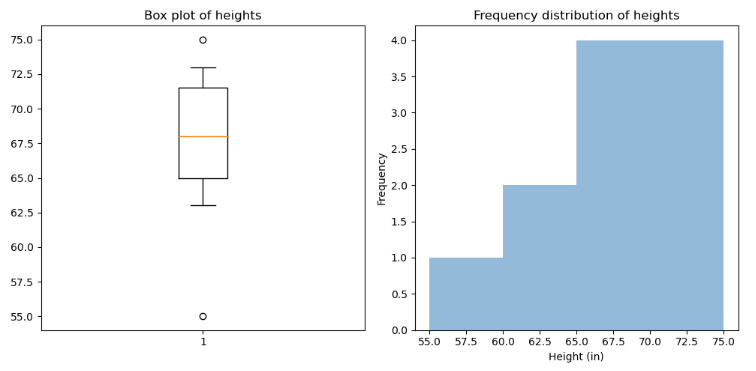
Screenshot of a box plot and histogram using Python.

Dit zijn enkele conclusies die we uit de resultaten kunnen trekken.

In de boxplot wordt de verdeling van de hoogten aan de linkerkant scheefgetrokken, wat betekent dat er veel personen zijn met hoogten die aanzienlijk lager zijn dan het gemiddelde.
Er zijn twee mogelijke uitbijters: 55 inch (4'7") en 75 inch (6'3"). Deze waarden zijn lager en hoger dan de rest van de gegevenspunten.
De verdeling van hoogten is ongeveer symmetrisch rond de mediaan, ervan uitgaande dat de uitbijters de distributie niet aanzienlijk scheeftrekken.

Bivariate- en multivariate-analyse

Bivariate- en multivariate-analyse helpt inzicht te krijgen in de relaties en interacties tussen verschillende variabelen in een gegevensset en worden vaak weergegeven met behulp van spreidingsdiagrammen, correlatiematrices of kruistabellen.

Spreidingsdiagrammen

De volgende code gebruikt de scatter() functie van matplotlib om het spreidingsplot te maken. We geven house_sizes op voor de x-as en house_prices voor de y-as.

import matplotlib.pyplot as plt
import numpy as np

# Sample data
np.random.seed(0)  # for reproducibility
house_sizes = np.random.randint(1000, 3000, size=50)  # Size of houses in square feet
house_prices = house_sizes * 100 + np.random.normal(0, 20000, size=50)  # Price of houses in dollars

# Create scatter plot
plt.scatter(house_sizes, house_prices)

# Set plot title and labels
plt.title('House Prices vs Size')
plt.xlabel('Size (sqt)')
plt.ylabel('Price ($)')

# Display the plot
plt.show()

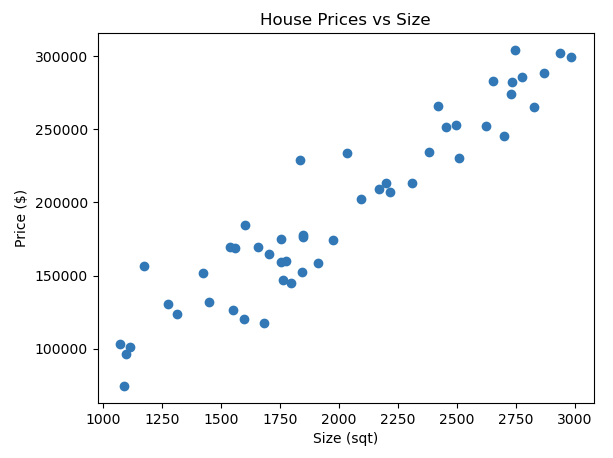
Screenshot of a scatter plot in a notebook.

In dit spreidingsplot vertegenwoordigt elk punt een huis. U ziet dat naarmate de grootte van het huis toeneemt (rechts langs de x-as beweegt), de prijs ook de neiging heeft om te stijgen (omhoog bewegen langs de y-as).

Dit type analyse helpt ons te begrijpen hoe wijzigingen in de afhankelijke variabelen van invloed zijn op de doelvariabele. Door de relaties tussen deze variabelen te analyseren, kunnen we voorspellingen doen over de doelvariabele op basis van de waarden van de afhankelijke variabelen.

Bovendien kan deze analyse helpen identificeren welke afhankelijke variabelen een aanzienlijke invloed hebben op de doelvariabele. Dit is handig voor functieselectie in machine learning-modellen, waarbij het doel is om de meest relevante functies te gebruiken om het doel te voorspellen.

Lijndiagram

Het volgende Python-script maakt gebruik van de matplotlib bibliotheek voor het maken van een lijndiagram van gesimuleerde huizenprijzen gedurende een periode van drie jaar. Het genereert een lijst met maandelijkse datums van 2020 tot 2022 en een bijbehorende lijst met huizenprijzen, die beginnen vanaf $ 200.000 en elke maand met enige willekeurigheid verhogen.

De x-as van de plot is opgemaakt om datums in de notatie Jaarmaand weer te geven en het interval van de tikken op de x-as in te stellen op elke zes maanden.

import matplotlib.pyplot as plt
from datetime import datetime, timedelta
import random
import matplotlib.dates as mdates

# Generate monthly dates from 2020 to 2022
dates = [datetime(2020, 1, 1) + timedelta(days=30*i) for i in range(36)]

# Generate corresponding house prices with some randomness
prices = [200000 + 5000*i + random.randint(-5000, 5000) for i in range(36)]

plt.figure(figsize=(10,5))

# Plot data
plt.plot(dates, prices)

# Format x-axis to display dates
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y-%m'))
plt.gca().xaxis.set_major_locator(mdates.MonthLocator(interval=6)) # set interval to 6 months
plt.gcf().autofmt_xdate() # Rotation

# Set plot title and labels
plt.title('House Prices Over Years')
plt.xlabel('Year-Month')
plt.ylabel('House Price ($)')

# Show the plot
plt.show()

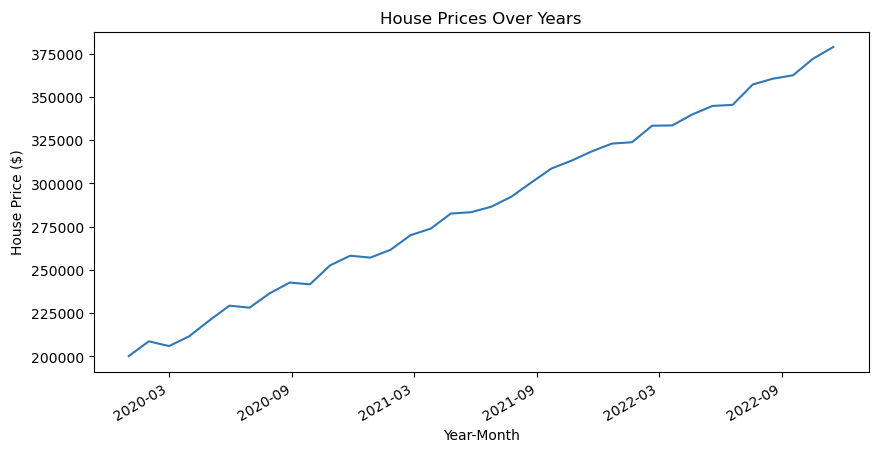
Screenshot of a line plot in a notebook.

Lijndiagrammen zijn eenvoudig te begrijpen en te lezen. Ze bieden een duidelijk overzicht op hoog niveau van de voortgang van de gegevens in de loop van de tijd, waardoor ze een populaire keuze zijn voor tijdreeksgegevens.

Paartekening

Een paarplot kan handig zijn als u de relatie tussen meerdere variabelen tegelijk wilt visualiseren.

import seaborn as sns
import pandas as pd

# Sample data
data = {
    'Size': [1000, 2000, 3000, 1500, 1200],
    'Bedrooms': [2, 4, 3, 2, 1],
    'Age': [5, 10, 2, 6, 4],
    'Price': [200000, 400000, 350000, 220000, 150000]
}

df = pd.DataFrame(data)

# Create a pair plot
sns.pairplot(df)

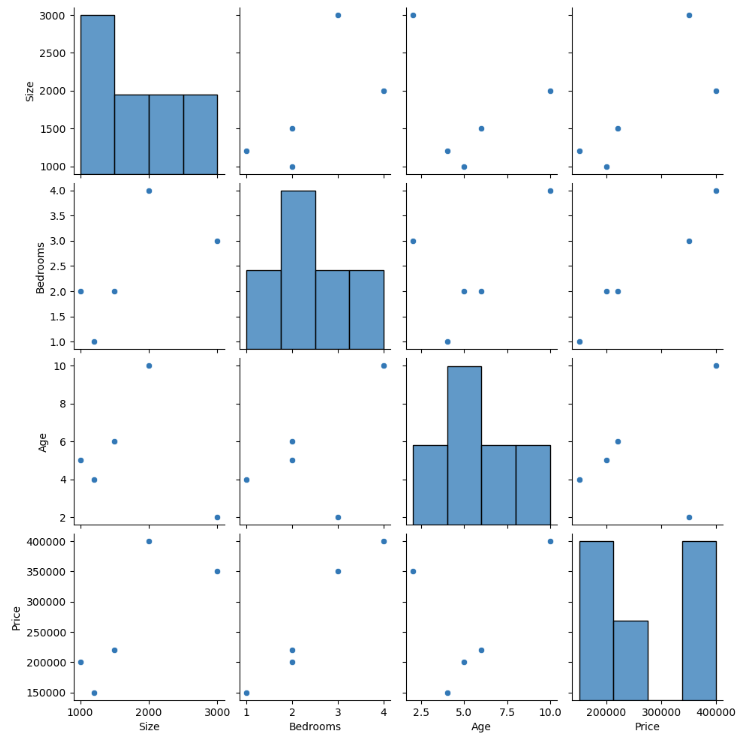
Screenshot of a pair plot in a notebook.

Hiermee maakt u een raster met plots waarin elke functie wordt uitgezet op elke andere functie. Op de diagonale zijn histogrammen met de verdeling van elke functie. De off-diagonale plots zijn spreidingsdiagrammen met de relatie tussen twee functies.

Dit soort visualisaties kan ons helpen begrijpen hoe verschillende functies met elkaar zijn verbonden en kunnen mogelijk worden gebruikt om beslissingen te nemen over het kopen of verkopen van huizen.