Inzicht in gegevensdistributie
Inzicht in de distributie van uw gegevens is essentieel voor effectieve gegevensanalyse, visualisatie en modelbouw.
Als een gegevensset een scheve verdeling heeft, betekent dit dat de gegevenspunten niet gelijkmatig zijn verdeeld en meer naar rechts of links leunen. Dit kan leiden tot een model dat gegevenspunten van ondervertegenwoordigde groepen onnauwkeurig voorspelt of wordt geoptimaliseerd op basis van een ongepaste metrische waarde.
Het belang van gegevensdistributie
Hier volgen belangrijke gebieden waarin inzicht in de distributie van uw gegevens de nauwkeurigheid van uw machine learning-modellen kan verbeteren.
| Stap | Beschrijving |
|---|---|
| Experimentele gegevensanalyse (EDA) | Inzicht in de distributie van gegevens maakt het verkennen van een nieuwe gegevensset en het vinden van patronen eenvoudiger. |
| Gegevensvoorverwerking | Sommige voorverwerkingstechnieken, zoals normalisatie of standaardisatie, worden gebruikt om de gegevens normaal gedistribueerd te maken. Dit is een algemene aanname in veel modellen. |
| Modelselectie | Verschillende modellen maken verschillende veronderstellingen over de distributie van de gegevens. Bij sommige modellen wordt er bijvoorbeeld van uitgegaan dat de gegevens normaal gesproken worden gedistribueerd en mogelijk niet goed presteren als deze aanname wordt geschonden. |
| Modelprestaties verbeteren | Het transformeren van uw doelvariabele om scheefheid te verminderen, kan uw doel lineair maken, wat handig is voor veel modellen. Dit kan het bereik van uw fout verminderen en de prestaties van uw model mogelijk verbeteren. |
| Relevantie van model | Zodra een model in productie is geïmplementeerd, is het belangrijk dat het relevant blijft in de context van de meest recente gegevens. Als er sprake is van scheeftrekken van gegevens, verandert de gegevensdistributie in de productie van wat tijdens de training is gebruikt, dan kan het model uit de context gaan. |
Inzicht in de gegevensdistributie kan uw modelbouwproces verbeteren. Hiermee kunt u nauwkeurigere veronderstellingen vaststellen door het gemiddelde, de verspreiding en het bereik van een willekeurige variabele in uw functies en het doel te identificeren.
Laten we eens kijken naar enkele van de meest voorkomende gegevensdistributietypen, zoals normale, binomiale en uniforme distributies.
Normale verdeling
Een normale verdeling wordt vertegenwoordigd door twee parameters: het gemiddelde en de standaarddeviatie. Het gemiddelde geeft aan waar de klokcurve is gecentreerd en de standaarddeviatie geeft de verspreiding van de verdeling aan.
Laten we een voorbeeld bekijken van een normale gedistribueerde functie. Met de onderstaande code worden de gegevens voor de var functie gegenereerd voor demonstratiedoeleinden.
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
# Set the mean and standard deviation
mu, sigma = 0, 0.1
# Generate a normally distributed variable
var = np.random.normal(mu, sigma, 1000)
# Create a histogram of the variable using seaborn's histplot
sns.histplot(var, bins=30, kde=True)
# Add title and labels
plt.title('Histogram of Normally Distributed Variable')
plt.xlabel('Value')
plt.ylabel('Frequency')
# Show the plot
plt.show()
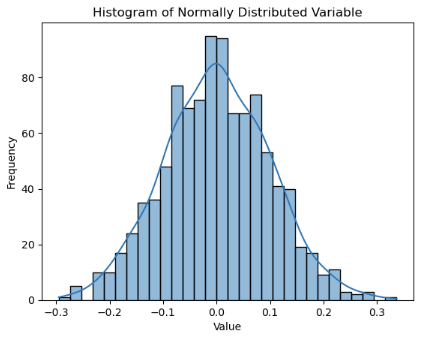
U ziet dat de var functie normaal gesproken wordt gedistribueerd, waarbij het gemiddelde en de mediaan (50% percentiel) naar verwachting meer of minder gelijk zijn. Voor scheve verdelingen leunt het gemiddelde meestal naar de zwaardere staart.
Dit zijn echter heuristische controles en daadwerkelijke bepaling worden gedaan met behulp van specifieke statistische tests zoals Shapiro-Wilk-test of Kolmogorov-Smirnov-test voor normaliteit.
Binomiale verdeling
Stel dat u wilt begrijpen hoe goed een bepaald kenmerk wordt waargenomen in een groep pinguïns.
U besluit om een gegevensset van 200 pinguïns te onderzoeken om te zien of ze van de Adelie-soorten zijn. Dit is een binomiaal distributieprobleem omdat er twee mogelijke resultaten zijn (Adelie of niet Adelie), een vast aantal experimenten (200 pinguïns) en elk proces onafhankelijk is van anderen.
Nadat u de gegevensset hebt geanalyseerd, merkt u dat 150 pinguïns van de Adelie-soorten zijn.
Als u weet dat uw gegevens een binomiale verdeling volgen, kunt u voorspellingen doen over toekomstige gegevenssets of groepen pinguïns. Als u bijvoorbeeld een andere groep van 200 pinguïns bestudeert, kunt u verwachten dat ongeveer 150 van de Adelie-soorten zijn.
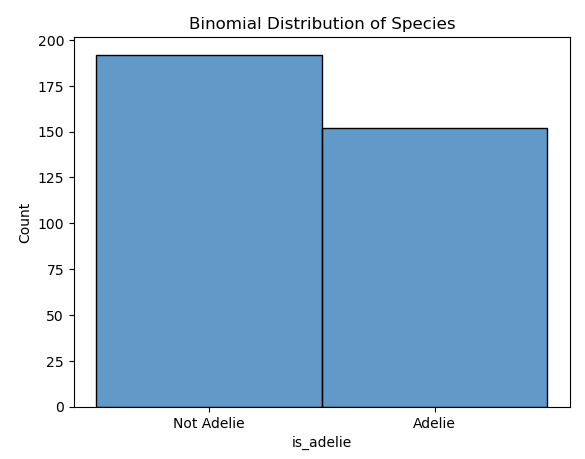
Met de volgende Python-code wordt een histogram van de is_adelie binomiale variabele uitgelezen. Het discrete=True argument zorgt sns.histplot ervoor dat de klassen worden behandeld als discrete intervallen. Dit betekent dat elke balk in het histogram exact overeenkomt met één categorie of booleaanse waarde, waardoor de plot gemakkelijker te interpreteren is.
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
# Load the Penguins dataset from seaborn
penguins = sns.load_dataset('penguins')
# Create a binomial variable for 'species'
penguins['is_adelie'] = np.where(penguins['species'] == 'Adelie', 1, 0)
# Plot the distribution of 'is_adelie'
sns.histplot(data=penguins, x='is_adelie', bins=2, discrete=True)
plt.title('Binomial Distribution of Species')
plt.xticks([0, 1], ['Not Adelie', 'Adelie'])
plt.show()
Uniforme verdeling
Een uniforme verdeling, ook wel een rechthoekige verdeling genoemd, is een soort waarschijnlijkheidsverdeling waarin alle resultaten even waarschijnlijk zijn. Elk interval van dezelfde lengte op de ondersteuning van de distributie heeft dezelfde waarschijnlijkheid.
import numpy as np
import matplotlib.pyplot as plt
# Generate a uniform distribution
uniform_data = np.random.uniform(-1, 1, 1000)
# Plot the distribution
plt.hist(uniform_data, bins=20, density=True)
plt.title('Uniform Distribution')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()
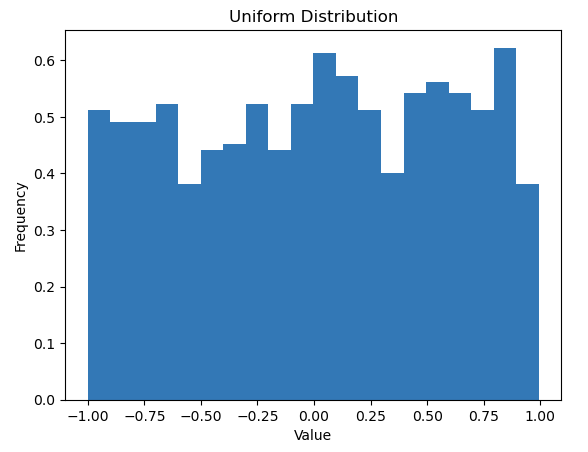
In deze code genereert de np.random.uniform functie 1000 willekeurige getallen die uniform worden verdeeld tussen -1 en 1. Het bins=30 argument geeft aan dat de gegevens moeten worden onderverdeeld in 30 bins en density=True zorgt ervoor dat het histogram wordt genormaliseerd om een waarschijnlijkheidsdichtheid te vormen. Dit betekent dat het gebied onder het histogram is geïntegreerd met 1, wat handig is bij het vergelijken van distributies.
Notitie
U krijgt waarschijnlijk verschillende resultaten als u de code meerdere keren uitvoert. Het basisidee van willekeurigheid is dat het onvoorspelbaar is en telkens wanneer u een steekproef neemt, u verschillende resultaten kunt krijgen.
U kunt dit proces beheren door een seed-waarde in te stellen met np.random.seed. Dit is erg handig voor het testen en opsporen van fouten in de fase van het bouwen van het model, omdat u hiermee dezelfde resultaten kunt reproduceren.