Resultaten van machine learning-modellen

In dit artikel worden verwarringsmatrixen, classificatieproblemen en nauwkeurigheid in modellen voor machine learning (ML) besproken. Het doel is om uw begrip van de nauwkeurigheid in ML-voorspellingsresultaten te vergroten. De doelgroep omvat technici, analisten en managers die hun kennis en vaardigheden in gegevenswetenschappen willen ontwikkelen.

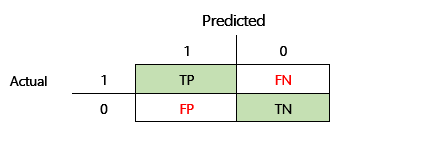
Verwarringsmatrix

Nadat een probleem met ML met toezicht is getraind op een reeks historische gegevens, wordt het getest met behulp van gegevens die zijn bewaard van het trainingsproces. Op deze manier kunt u de voorspellingen van het getrainde model vergelijken met de werkelijke waarden. De verwarringsmatrix biedt een manier om te evalueren hoe succesvol een classificatieprobleem is en waar het fouten oplevert (dat wil zeggen dat het tot verwarring leidt).

Uw doelstelling is bijvoorbeeld om te voorspellen of een huisdier een hond of een kat is op basis van bepaalde fysieke en gedragskenmerken. Als u een testgegevensset hebt die 30 honden en 20 katten bevat, kan de verwarringsmatrix er als volgt uitzien:

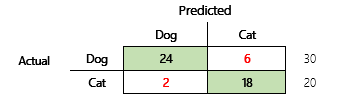
De getallen in de groene cellen vertegenwoordigen de juiste voorspellingen. Zoals u ziet, heeft het model een hoger percentage van de werkelijke katten juist voorspeld. De algehele nauwkeurigheid van het model is eenvoudig te berekenen. In dit geval is het 42 ÷ 50 of 0,84.

Classificaties met meerdere klassen in een verwarringsmatrix

De meeste discussies over de verwarringsmatrix zijn gericht op binaire classificaties, zoals in het vorige voorbeeld. Dit is een speciaal geval waarin andere metrische gegevens kunnen worden overwogen, zoals gevoeligheid en relevante overeenkomsten.

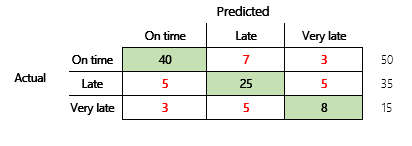
Vervolgens kijken we naar een classificatieprobleem voor een financieringsscenario met drie statussen. Het model voorspelt of een klantfactuur op tijd, laat of zeer laat wordt betaald. Voorbeeld: van de 100 testfacturen, worden 50 op tijd betaald, 35 laat en 15 zeer laat. In dit geval kan een model een verwarringsmatrix produceren die vergelijkbaar is met de volgende afbeelding.

]

Een verwarringsmatrix geeft beduidend meer informatie dan een eenvoudige nauwkeurigheidswaarde. Het is echter nog relatief eenvoudig te begrijpen. Een verwarringsmatrix geeft aan of u een evenwichtige gegevensset hebt waarin de uitvoerklassen vergelijkbare aantallen hebben. Voor het scenario met meerdere klassen wordt u geïnformeerd hoe ver een voorspelling er naast kan zitten wanneer de uitvoerklassen ordinaal zijn, zoals in het vorige voorbeeld over klantbetalingen.

Modelnauwkeurigheid

Verschillende metrische nauwkeurigheidsgegevens hebben het voordeel dat ze de kwaliteit van het model kwantificeren.

Omdat metrische nauwkeurigheidsgegevens gemakkelijk te begrijpen zijn, is het een goed uitgangspunt voor het uitleggen van een model aan andere mensen, vooral aan gebruikers van het model die geen gegevenswetenschappers zijn. Er is geen begrip over statistieken nodig om inzicht te krijgen in de nauwkeurigheid van het model. Wanneer een verwarringsmatrix beschikbaar is, verschaft het meer inzicht in de prestaties van het model.

Voor een grondiger begrip moeten echter verschillende uitdagingen worden opgemerkt die verband houden met de nauwkeurigheid. De bruikbaarheid van de metrische gegevens is afhankelijk van de context van het probleem. De vraag die vaak wordt gesteld met betrekking tot modelprestaties is: 'Hoe goed is het model' Het antwoord op deze vraag is echter niet noodzakelijkerwijs eenvoudig. We bekijken de volgende verwarringsmatrix (model 2).

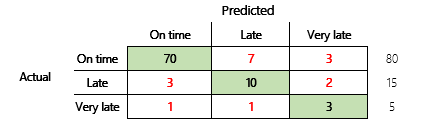
Een snelle berekening laat zien dat de nauwkeurigheid van dit model (70 + 10 + 3) ÷ 100 of 0,83 is. Oppervlakkig gezien lijkt dit resultaat beter dan het resultaat van het vorige model met meerdere klassen (model 1) met een nauwkeurigheid van 0,73. Maar is het beter?

We beginnen bij deze vraag met eerst naar de nauwkeurigheid van een naïeve inschatting te kijken. Voor een classificatieprobleem zal een eenvoudige inschatting altijd de meest gangbare klasse voorspellen. Voor model 1 is dat "op tijd" en wordt een nauwkeurigheid van 0,50 geleverd. Voor model 2 is dat ook "op tijd" en wordt een nauwkeurigheid van 0,80 geleverd. Omdat model 1 de naïeve inschatting van 0,73 – 0,50 = 0,23 verbetert, terwijl model 2 de naïeve inschatting verbetert met 0,83 – 0,80 = 0,03, is model 1 een beter model, zelfs als het een lagere nauwkeurigheid heeft. De berekening laat zien dat een effectieve beoordeling van de kwaliteit van een model meer context vereist dan de nauwkeurigheidswaarde.

Ook moet er rekening worden gehouden met een ander aspect. Overweeg een scenario waarbij een medische test wordt gebruikt om een ziekte in een patiënt te detecteren. Dit probleem is een probleem met een binaire classificatie waarbij een positief resultaat aangeeft dat de patiënt de ziekte heeft. In dit scenario moet u nadenken over de gevolgen van de volgende fouten:

• Onjuiste positieven, waarbij de test aangeeft dat een patiënt de ziekte heeft, maar deze niet echt heeft.
• Onjuiste negatieven, waarbij de test aangeeft dat een patiënt de ziekte niet heeft, terwijl deze wel heeft.

Uiteraard zijn beide typen fouten niet gewenst, maar welke is erger? Ook is dat hier afhankelijk van de situatie. Bij een levensbedreigende ziekte die snelle behandeling vereist, heeft het minimaliseren van foute negatieven (hopelijk gevolgd door extra tests) voorrang. In andere, minder kritieke situaties kunnen de makers van modellen in plaats hiervan foute positieven minimaliseren. In ieder geval is het een redelijke conclusie dat de kwaliteit van een model alleen effectief kan worden bepaald als u meer informatie hebt dan de metrische nauwkeurigheidsgegevens.

Aanbevelingen

Nauwkeurigheid is een belangrijk hulpmiddel voor de communicatie met domeinexperts die niet vertrouwd zijn met statistieken. Als u de informatie echter nuttig wilt maken, is het van cruciaal belang dat er aanvullende context samen met de nauwkeurigheidswaarde wordt geleverd.

Voor het betalingsvoorspellingsscenario kunt u een doel stellen voor het ML-model dat factoren in verschillende betalingsgedragingen bevat. Het doel is dat het model bij een naïeve inschatting moet worden verbeterd door het aantal onjuiste antwoorden met ten minste 50 procent te verminderen. Met andere woorden, u richt zich op een nauwkeurigheid die het verschil tussen de nauwkeurigheid van een naïeve inschatting en 100 procent splitst.

De volgende tabel geeft een overzicht van dit principe voor de verwarringsmatrixen in dit artikel.

Model	Naïeve inschatting	Doel	Modelnauwkeurigheid	Is het doel bereikt?
Model 1	0.50	0.75	0.73	Bijna. Dit model verbetert de inschatting aanzienlijk.
Model 2	0.80	0.90	0.83	Nr. Verbetering vereist.

F1-nauwkeurigheid classificatie

De laatste overweging in dit artikel is een meer geavanceerde maatstaf van ML-prestaties voor classificatie, bekend als F1-nauwkeurigheid.

Voordat de F1-nauwkeurigheid kan worden gedefinieerd, moeten er twee extra metrieken worden geïntroduceerd: precisie en relevante overeenkomsten. Precisie geeft aan hoeveel van het totale aantal voorspellingen dat als positief is opgegeven, correct is toegewezen. Deze metriek wordt ook wel de positieve voorspellende waarde genoemd. Relevante overeenkomsten is het totaal aantal werkelijke positieve gevallen dat correct is voorspeld. Deze metriek wordt ook wel de gevoeligheid genoemd.

In de verwarringsmatrix in de voorgaande afbeelding worden deze metrische gegevens op de volgende manier berekend:

• Precisie = TP ÷ (TP + FP)
• Relevante overeenkomsten = TP ÷ (TP + FN)

Bij de F1-meting worden precisie en relevante overeenkomsten gecombineerd. Het resultaat is het harmonische gemiddelde van de twee waarden. Dit wordt als volgt berekend:

• F1 = 2 × (precisie x relevante overeenkomsten) ÷ (precisie + relevante overeenkomsten)

We kijken naar een concreet voorbeeld. Eerder in dit artikel is er een voorbeeld van een model waarin werd voorspeld of een dier een hond of een kat was. De afbeelding wordt hier herhaald.

Dit zijn de resultaten als "hond" wordt gebruikt als het positieve antwoord.

• Precisie = 24 ÷ (24 + 2) = 0,9231
• Relevante overeenkomsten = 24 ÷ (24 + 6) = 0,8
• F1 = 2 × (0,9231 × 0,8) ÷ (0,9231 + 0,8) = 0,8572

Zoals u ziet, ligt de F1-waarde tussen de waarden voor precisie en relevante overeenkomsten.

Hoewel F1-nauwkeurigheid niet zo eenvoudig te begrijpen is, wordt hiermee nuance aan het basisnauwkeurigheidsaantal toegevoegd. Het kan ook helpen met gegevenssets die niet in evenwicht zijn, zoals in de volgende discussie wordt weergegeven.

In de sectie Modelnauwkeurigheid van dit artikel werden de volgende twee verwarringsmatrixen vergeleken. Hoewel het eerste model minder nauwkeurig is, was het een nuttiger model omdat het beter is dan de standaardinschatting van een 'op tijd'-betaling.

Laten we eens kijken hoe deze twee modellen zich tot elkaar verhouden wanneer de F1-score wordt gebruikt. De F1-score houdt rekening met precisie en relevante overeenkomsten voor elke status, en met de F1-macroberekening wordt vervolgens het gemiddelde van de F1-score over de statussen bepaald om een algemene F1-score te bepalen. Er zijn andere F1-varianten, maar het is interessanter de macroversie te overwegen, gezien de gelijke inachtneming van alle drie de statussen.

Om de berekeningen te vereenvoudigen, worden samplematrixen gebouwd om de werkelijke en voorspelde waarden te vergelijken. Deze matrixen hebben gebruik gemaakt van de metrische bibliotheek van sklearn in Python om de waarden te berekenen. Hier volgt het resultaat.

Model	Naïeve inschatting	Nauwkeurigheid	F1-macro
Model 1	0.5	0.73	0.67
Model 2	0.80	0.83	0.66

Hier volgt het sklearn.metrics-classificatierapport voor model 1 voor meer informatie over hoe deze berekening werkt. De drie statussen, 'op tijd', 'laat' en 'zeer laat', worden aangegeven door de rijen met respectievelijk de namen 1, 2 en 3. Het macrogemiddelde is gewoon het gemiddelde van de kolom ' f1-score'.

	precisie	relevante overeenkomsten	f1-score
1	0.83	0.80	0.82
2	0.68	0.71	0.69
3	0.50	0.50	0.50

Zoals deze resultaten aangeven, hebben de twee modellen bijna dezelfde F1-macronauwkeurigheidsscores. In deze en vele andere gevallen biedt de F1-nauwkeurigheid een betere indicatie van de mogelijkheden van een model. Net als voor de nauwkeurigheid vereist de interpretatie van de resultaten dat u begrijpt wat het belangrijkst is om in het model te overwegen.