부록: 매트릭스 변환

이 항목에서는 2-D 그래픽의 행렬 변환을 수학적으로 간략하게 살펴봅니다. 그러나 Direct2D에서 변환을 사용하기 위해 행렬 수학을 알 필요는 없습니다. 수학에 관심이 있는 경우 이 항목을 읽어 보세요. 그러지 않으면 이 항목을 건너뛰어도 됩니다.

• 행렬 소개
  • 행렬 연산
• 아핀 변환
  • 이동 변환
  • 스케일링 변환
  • 원점을 중심으로 회전
  • 임의 지점을 중심으로 회전
  • 기울이기 변환
• Direct2D에서 변환 표현
• 다음

행렬 소개

행렬은 실수의 직사각형 배열입니다. 행렬의 차수는 행과 열의 수입니다. 예를 들어 행렬에 3개의 행과 2개의 열이 있는 경우 차수는 3 × 2입니다. 행렬은 일반적으로 대괄호로 묶인 행렬 요소와 함께 표시됩니다.

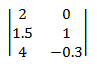
표기법: 행렬은 대문자로 지정됩니다. 요소는 소문자로 지정됩니다. 첨자는 요소의 행과 열 번호를 나타냅니다. 예를 들어 aij는 행렬 A의 i번째 행과 j번째 열에 있는 요소입니다.

다음 다이어그램은 행렬의 각 셀에 개별 요소가 있는 i × j 행렬을 보여 줍니다.

행렬 연산

이 섹션에서는 행렬에 정의된 기본 연산에 대해 설명합니다.

덧셈. 두 행렬의 합계 A + B는 A와 B의 해당 요소를 더해서 얻어집니다.

A + B = \[ a*ij* \] + \[ b*ij* \] = \[ a*ij* + b*ij* \]

스칼라 곱셈. 이 연산은 행렬에 실수를 곱합니다. 실수 k가 주어지면 스칼라 곱인 kA는 A의 모든 요소에 k를 곱하여 얻어집니다.

kA = k\[ a*ij* \] = \[ k × a*ij* \]

행렬 곱셈. 차수가 (m × n) 및 (n × p)인 두 개의 행렬 A와 B가 주어지면 곱인 C = A × B는 다음과 같이 정의되는 차수가 (m × p)인 행렬입니다

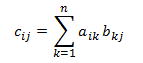
또는 다음과 같습니다.

c*ij* = a*i*1 x b1*j* + a*i*2 x b2*j* + ... + a*in* + b*nj*

즉, 각 요소 cij를 계산하려면 다음을 수행합니다.

1. A의 i번째 행과 B의 j번째 열을 가져옵니다.
2. 행과 열의 각 요소 쌍을 곱합니다. 첫 번째 행 항목은 첫 번째 열 항목, 두 번째 행 항목은 두 번째 열 항목과 곱하는 방식입니다.
3. 결과를 합산합니다.

다음은 (2 × 2) 행렬과 (2 × 3) 행렬을 곱하는 예제입니다.

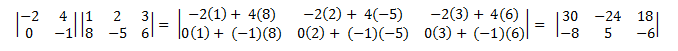
행렬 곱 가환 적 아닙니다. 즉, A × B ≠ B × A입니다. 또한 정의상 모든 행렬 쌍을 곱할 수 있는 것은 아닙니다. 왼쪽 행렬의 열 수는 오른쪽 행렬의 행 수와 같아야 합니다. 그러지 않으면 × 연산자가 정의되지 않습니다.

단위 행렬. 단위 행렬은 I로 지정되었으며 다음과 같이 정의된 정사각형 행렬입니다.

*i* = *j*이면 I*ij* = 1이고, 그러지 않으면 0입니다.

즉, 단위 행렬은 행 번호가 열 번호와 같은 각 요소에 대해 1을 포함하고 다른 모든 요소에 대해 0을 포함합니다. 예를 들어 다음은 3 × 3 단위 행렬입니다.

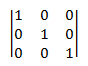
다음 등식은 모든 행렬 M에 대해 유지됩니다.

M x I = M I x M = M

아핀 변환

아핀 변형은 한 좌표 공간을 다른 좌표 공간에 매핑하는 수학 연산입니다. 즉, 한 점 집합을 다른 점 집합에 매핑합니다. 아핀 변환에는 컴퓨터 그래픽에서 유용하게 사용할 수 있는 몇 가지 기능이 있습니다.

• 아핀 변환은 공선성을 유지합니다. 3개 이상의 점이 선에 있으면 변환 후에도 여전히 선을 형성합니다. 직선은 직선으로 유지됩니다.
• 두 아핀 변환의 구성은 아핀 변환입니다.

2-D 공간에 대한 아핀 변환의 형식은 다음과 같습니다.

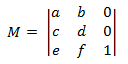
앞에서 설명한 행렬 곱셈의 정의를 적용하면 두 아핀 변환의 곱이 또 다른 아핀 변환임을 보여 줄 수 있습니다. 아핀 변환을 사용하여 2D 점을 변환하기 위해 점은 1 × 3 행렬로 표시됩니다.

P = \| x y 1 \|

처음 두 요소에는 점의 x 및 y 좌표가 포함됩니다. 1은 수학이 올바르게 작동하도록 세 번째 요소에 배치됩니다. 변환을 적용하려면 다음과 같이 두 행렬을 곱합니다.

P' = P × M

이는 다음으로 확장됩니다.

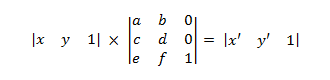
라는 설치 관리자 실행 파일에 포함됩니다. 여기서

x' = ax + cy + e y' = bx + dy + f

변환된 점을 가져오려면 행렬 P'의 처음 두 요소를 사용합니다.

p = (x', y') = (ax + cy + e, bx + dy + f)

참고

1 × n 행렬을 행 벡터라고 합니다. Direct2D와 Direct3D는 모두 행 벡터를 사용하여 2D 또는 3D 공간의 점을 나타냅니다. 열 벡터(n × 1)를 사용하고 변환 행렬을 전치하면 동일한 결과를 얻을 수 있습니다. 대부분의 그래픽 텍스트는 열 벡터 형식을 사용합니다. 이 항목에서는 Direct2D 및 Direct3D와의 일관성을 위해 행 벡터 양식을 제공합니다.

 

다음 몇 개의 섹션은 기본 변환을 유도합니다.

이동 변환

이동 변환 매트릭스의 형식은 다음과 같습니다.

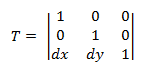
점 P를 이 식에 대입하면 다음과 같은 결과가 나옵니다.

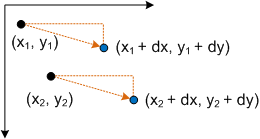
P' = (*x* + *dx*, *y* + *dy*)

X축의 dx와 Y축의 dy로 변환된 점 (x, y)에 해당합니다.

스케일링 변환

스케일링 변환 행렬의 형식은 다음과 같습니다.

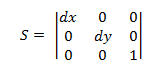
점 P를 이 식에 대입하면 다음과 같은 결과가 나옵니다.

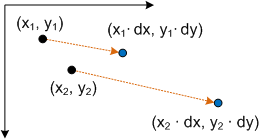
P' = (*x* ∙ *dx*, *y* ∙ *dy*)

이는 dx 및 dy로 스케일링된 점 (x, y)에 해당합니다.

원점을 중심으로 회전

원점을 중심으로 점을 회전하는 행렬의 형식은 다음과 같습니다.

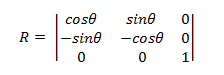
변환된 지점은 다음과 같습니다.

P' = (*x*cosΘ – ysinΘ, *x*sinΘ + *y*cosΘ)

증명. P'가 회전을 나타낸다는 것을 표시하려면 다음 다이어그램을 고려하세요.

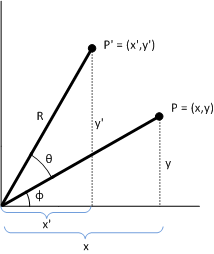
지정된 조건:

P = (x,y)

변환할 원래 점입니다.

Φ

선(0, 0)에서 P까지의 각도입니다.

Θ

원점에서 (x, y)를 회전할 각도입니다.

P' = (x',y')

변환된 점입니다.

R

P까지의 선 (0, 0)의 길이입니다. 또한 회전하는 원의 반경입니다.

참고

이 다이어그램은 양의 y축이 위를 가리키는 기하학에 사용되는 표준 좌표계를 사용합니다. Direct2D는 양의 y축이 아래쪽을 가리키는 Windows 좌표계를 사용합니다.

 

x축과 P'까지의 선 (0, 0) 사이의 각도는 Φ + Θ입니다. 다음 항등식이 성립합니다.

x = R cosΦ y = R sinΦ x' = R cos(Φ + Θ) y' = R sin(Φ+ Θ)

이제 Θ로 x'와 y'를 풉니다. 삼각법 덧셈 수식 기준:

x' = R(cosΦcosΘ – sinΦsinΘ) = RcosΦcosΘ – RsinΦsinΘ y' = R(sinΦcosΘ + cosΦsinΘ) = RsinΦcosΘ + RcosΦsinΘ

빼면 다음을 얻습니다.

x' = xcosΘ – ysinΘ y' = xsinΘ + ycosΘ

이는 이전에 표시된 변환된 지점 P'에 해당합니다.

임의 지점을 중심으로 회전

원점 이외의 점 (x, y)를 중심으로 회전하려면 다음 행렬이 사용됩니다.

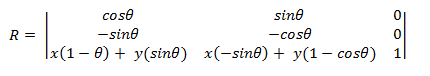
점 (x, y)를 원점으로 하여 이 행렬을 유도할 수 있습니다.

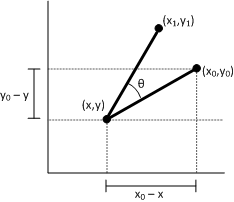
점 (x0, y0)을 점 (x, y)를 중심으로 회전한 결과가 (x1, y1)라고 합니다. 다음과 같이 x1을 유도할 수 있습니다.

x1 = (x0 – x)cosΘ– (y0 – y)sinΘ + x x1 = x0cosΘ – y0sinΘ + \[ (1 – cosΘ) + ysinΘ \]

이제 이전의 x1 = ax0 + cy0 + e 수식을 사용하여 이 수식을 변환 행렬에 다시 연결합니다. 동일한 절차를 사용하여 y1을 도출합니다.

기울이기 변환

기울이기 변환은 네 가지 매개 변수로 정의됩니다.

• Θ: x축을 따라 기울이는 양으로, y축으로부터의 각도로 측정됩니다.
• Φ: y축을 따라 기울이는 양으로, x축으로부터의 각도로 측정됩니다.
• (px, py): 기울이기가 수행되는 지점의 x 및 y 좌표입니다.

기울이기 변환은 다음 행렬을 사용합니다.

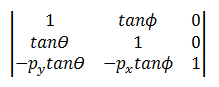
변환된 지점은 다음과 같습니다.

P' = (*x* + *y*tanΘ – *py*tanΘ, *y* + *x*tanΦ) – *py*tanΦ

또는 다음과 같습니다.

P' = (*x* + (*y* – *py*)tanΘ, *y* + (*x* – *px*)tanΦ)

이 변환이 어떻게 작동하는지 보려면 각 구성 요소를 개별적으로 고려합니다. Θ 매개 변수는 x 방향의 모든 점을 tanΘ와 같은 양만큼 이동합니다. 다음 다이어그램은 Θ와 x축 기울이기 사이의 관계를 보여 줍니다.

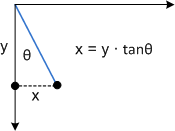
다음은 직사각형에 적용된 동일한 기울이기입니다.

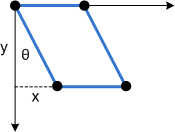
Φ 매개 변수는 효과가 동일하지만 y축을 따릅니다.

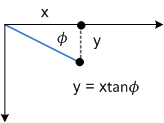
다음 다이어그램은 wlr사각형에 적용된 y축 기울이기를 보여 줍니다.

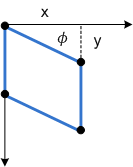
마지막으로 px 및 py 매개 변수는 x축과 y축을 따라 기울이기의 중심점을 이동합니다.

Direct2D에서 변환 표현

모든 Direct2D 변환은 아핀 변환입니다. Direct2D는 비아핀 변환을 지원하지 않습니다. 변환은 D2D1_MATRIX_3X2_F 구조체로 표시됩니다. 이 구조체는 3 × 2 행렬을 정의합니다. 아핀 변환의 세 번째 열은 항상 동일하고([0, 0, 1]), Direct2D가 비아핀 변환을 지원하지 않으므로 전체 3 × 3 행렬을 지정할 필요가 없습니다. 내부적으로 Direct2D는 3 × 3 행렬을 사용하여 변환을 계산합니다.

D2D1_MATRIX_3X2_F의 멤버는 인덱스 위치에 따라 이름이 지정됩니다. _11 멤버는 요소 (1, 1)이고 _12 멤버는 요소 (1, 2)입니다. 구조체 멤버를 직접 초기화할 수 있지만 D2D1::Matrix3x2F 클래스를 사용하는 것이 좋습니다. 이 클래스는 D2D1_MATRIX_3X2_F를 상속하고 기본 아핀 변환을 만들기 위한 도우미 메서드를 제공합니다. 이 클래스는 Direct2D에서 변환 적용에 설명된 대로 둘 이상의 변환을 구성하기 위한 operator*()도 정의합니다.

다음

모듈 4. 사용자 입력