양자 컴퓨팅에서 중첩이란?
이전 단원의 고양이가 양자 고양이라면 양자 고양이와 상자 시스템의 상태는 동일합니다. 즉, 상자 측면에서 양자 고양이의 6가지 위치의 합계에 해당 위치에서 양자 고양이를 찾을 확률이 가중치로 적용됩니다. 유일한 차이점은 클래식 고양이가 6개의 가능한 위치 중 하나에(만) 있을 수 있으며 양자 고양이는 동시에 6개의 모든 위치에 있을 수 있다는 것입니다.
클래식 세계에서 개체는 한 번에 하나의 상태로만 있을 수 있습니다. 그러나 양자 세계에서 양자 입자는 동시에 여러 상태로 있을 수 있습니다. 이 현상을 중첩이라고 합니다.
양자 컴퓨팅에서는 슬프게도 아무도 양자 고양이를 사용하지 않고 큐비트를 사용합니다. "큐비트"라는 단어는 "양자 비트"를 의미합니다. 정보의 기본 단위가 비트인 클래식 컴퓨팅과 마찬가지로, 양자 컴퓨팅에서는 정보의 기본 단위가 큐비트입니다. 비트가 0과 1이라는 두 가지 가능한 값을 사용할 수 있는 것처럼 큐비트는 두 가지 가능한 상태에 존재할 수 있는 양자 입자입니다. 예를 들어 큐비트는 두 방향으로 편광될 수 있는 광자이거나, 두 에너지 레벨에 있을 수 있는 전자일 수 있습니다.
큐비트에서는 중첩을 어떻게 나타낼 수 있나요? 특정 상태에서 큐비트를 찾을 확률은 얼마나 되나요?
큐비트에서는 중첩을 어떻게 나타낼 수 있나요?
큐비트는 두 개의 가능한 위치 또는 상태를 갖는 양자 입자입니다. 클래식 비트와 유사하게 큐비트에서 양자 상태를 $0$ 및 $1$이라고도 합니다. 큐비트는 상태 $0$ 또는 상태 $1$이거나 두 상태의 중첩 상황에 있을 수 있습니다. 이 중첩을 어떻게 나타낼 수 있나요?
가운데 점이 원의 중심이 되도록 원과 세로 및 가로 축을 그린다고 가정해 보겠습니다. 상태 $0$은 세로 축의 위쪽 점에 배치되고 상태 $1$은 아래쪽 점에 있습니다.
이 표현을 어떻게 설명할 수 있나요? $0$ 상태는 화살표 또는 위쪽을 가리키는 벡터이로, $1$은 아래쪽을 가리키는 벡터라고 말할 수 있습니다. 따라서 클래식 비트는 위쪽 또는 아래쪽을 가리키는 벡터이지만 다른 방향을 가리키지 않습니다.
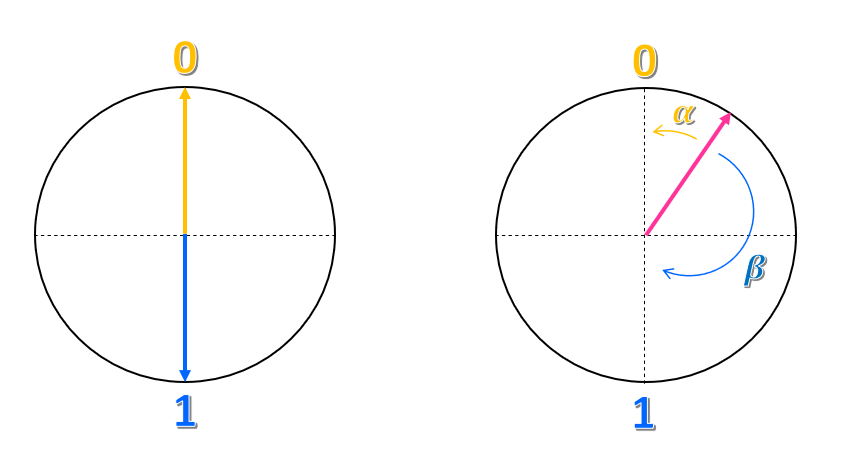
원의 다른 점은 어떤가요? 해당 상태를 어떻게 나타낼 수 있나요? 평면의 좌표와 마찬가지로 두 상태 $0$ 및 $1$의 조합으로 나타낼 수 있습니다. 예를 들어 벡터가 $0$ 상태에서 얼마나 가까운지를 나타내는 각도를 $\alpha$라고 지칭하고, $1$ 상태에서 얼마나 가까운지를 나타내는 각도를 $\beta$라고 지칭할 수 있습니다. 이 상태를 $\alpha 0 + \beta 1 $로 나타낼 수 있습니다. 따라서 이 상태는 상태 $0$과 $1$의 중첩입니다.
고양이 및 상자의 예와 마찬가지로 큐비트의 전역 상태는 개별 상태 $0$과 $1$의 합계에 해당 상태에서 큐비트를 찾을 확률인 $\alpha$ 및 $\beta $를 가중치로 적용합니다.
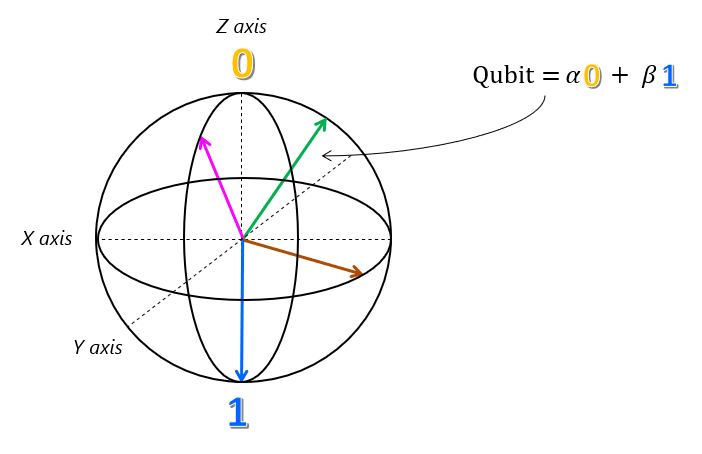
큐비트의 이러한 표현은 실제로 정확하며 블로흐 구로 알려져 있습니다.
팁
블로흐 구는 큐비트에서 수행할 수 있는 연산을 카디널 축 중 하나에 대한 회전으로 나타낼 수 있으므로 강력한 도구입니다. 회전 시퀀스로서 양자 계산을 고려하는 것은 강력한 직관력이지만, 이 직관력을 사용하여 알고리즘을 설계하고 설명하는 것은 어렵습니다. Q#은 이러한 회전을 설명하는 언어를 제공하여 이 문제를 완화합니다.
한 상태에서 큐비트를 찾을 확률은 얼마나 되나요?
이전 단원에 나온 고양이 및 상자의 예와 마찬가지로 큐비트의 전역 상태는 개별 상태 $0$과 $1$의 합계에 해당 상태에서 큐비트를 찾을 확률인 $\alpha$ 및 $\beta $를 가중치로 적용합니다. $\alpha$ 및 $\beta$는 큐비트 상태가 각각 $0$ 및 $1$에 얼마나 "가까운"지를 나타냅니다. 그렇다면 $\alpha$ 및 $\beta$는 $0$ 또는 $1$ 상태에서 큐비트를 찾을 확률인가요? 그렇지 않습니다.
숫자 $\alpha$ 및 $\beta$는 각 상태에 대한 확률 진폭입니다. 그 절대값(예: $|\alpha|^2$)을 제곱하면 해당 확률을 얻습니다. 예를 들어 $0$ 상태를 관찰할 확률은 $|\alpha|^2$이고 $1$ 상태를 관찰할 확률은 $|\beta|^2$입니다.
숫자 $\alpha$ 및 $\beta$는 양수, 음수, 심지어 복소수일 수 있습니다. 그러나 유효한 양자 중첩에서 모든 확률의 합계는 1, 즉 $|\alpha|^2+|\beta|^2=1$입니다. 이 제약 조건은 정규화 조건이라고 합니다. 정규화 조건을 측정 시 결과를 항상 얻을 수 있다고 생각할 수 있으므로 모든 가능한 결과를 측정하는 확률의 합은 1이 되어야 합니다.