SkiaSharp의 행렬 변환
다재다능한 변환 매트릭스를 사용하여 SkiaSharp 변환에 대해 자세히 알아보기
개체에 적용된 SKCanvas 모든 변환은 구조체의 SKMatrix 단일 인스턴스에 통합됩니다. 이는 모든 최신 2D 그래픽 시스템과 유사한 표준 3x3 변환 매트릭스입니다.
앞에서 본 것처럼 변형 매트릭스에 대해 모르고 SkiaSharp에서 변환을 사용할 수 있지만, 변환 행렬은 이론적인 관점에서 중요하며, 변환을 사용하여 경로를 수정하거나 복잡한 터치 입력을 처리할 때 중요합니다. 이 두 가지 모두 이 문서와 다음 문서에서 설명합니다.

현재 적용된 SKCanvas 변환 매트릭스는 읽기 전용 TotalMatrix 속성에 액세스하여 언제든지 사용할 수 있습니다. 메서드를 사용하여 새 변환 매트릭스를 SetMatrix 설정할 수 있으며 해당 변환 매트릭스를 호출 ResetMatrix하여 기본값으로 복원할 수 있습니다.
캔버스의 행렬 변환과 직접 작동하는 유일한 멤버 SKCanvas 는 Concat 두 행렬을 함께 곱하여 연결하는 것입니다.
기본 변환 매트릭스는 ID 행렬이며 대각선 셀에 1과 0으로 구성됩니다.
| 1 0 0 | | 0 1 0 | | 0 0 1 |
정적 SKMatrix.MakeIdentity 메서드를 사용하여 ID 행렬을 만들 수 있습니다.
SKMatrix matrix = SKMatrix.MakeIdentity();
SKMatrix 기본 생성자는 ID 행렬을 반환하지 않습니다. 모든 셀이 0으로 설정된 행렬을 반환합니다. 이러한 셀을 SKMatrix 수동으로 설정하려는 경우가 아니면 생성자를 사용하지 마세요.
SkiaSharp에서 그래픽 개체를 렌더링할 때 각 점(x, y)은 세 번째 열에 1이 있는 1x3 행렬로 효과적으로 변환됩니다.
| x y 1 |
이 1 x 3 행렬은 Z 좌표가 1로 설정된 3차원 점을 나타냅니다. 2차원 행렬 변환에 3차원으로 작업해야 하는 수학적 이유가 있습니다(나중에 설명). 이 1 x 3 행렬은 3D 좌표계의 점을 나타내는 것으로 생각할 수 있지만 Z가 1인 2D 평면에는 항상 있습니다.
그런 다음 이 1-3 행렬에 변환 행렬을 곱하면 캔버스에 렌더링되는 점이 생성됩니다.
| 1 0 0 |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
표준 행렬 곱셈을 사용하면 변환된 지점은 다음과 같습니다.
x' = x
y' = y
z' = 1
이것이 기본 변환입니다.
메서드가 Translate 개체에 호출되면 메서드에 tx 대한 SKCanvas 인수 Translate 는 ty 변환 행렬의 세 번째 행에서 처음 두 개의 셀이 됩니다.
| 1 0 0 | | 0 1 0 | | tx ty 1 |
이제 곱하기는 다음과 같습니다.
| 1 0 0 |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| tx ty 1 |
변환 수식은 다음과 같습니다.
x' = x + tx
y' = y + ty
배율 인수의 기본값은 1입니다. 새 개체에서 Scale 메서드를 호출하면 결과 변환 행렬에 대각선 셀의 sx 인수와 sy 인수가 포함 SKCanvas 됩니다.
| sx 0 0 |
| x y 1 | × | 0 sy 0 | = | x' y' z' |
| 0 0 1 |
변환 수식은 다음과 같습니다.
x' = sx · x
y' = sy · y
호출 Skew 후의 변환 행렬에는 배율 인수에 인접한 행렬 셀에 다음 두 인수가 포함됩니다.
│ 1 ySkew 0 │
| x y 1 | × │ xSkew 1 0 │ = | x' y' z' |
│ 0 0 1 │
변환 수식은 다음과 같습니다.
x' = x + xSkew · y
y' = ySkew · x + y
α 각도에 RotateDegreesRotateRadians 대한 호출의 경우 변환 행렬은 다음과 같습니다.
│ cos(α) sin(α) 0 │
| x y 1 | × │ –sin(α) cos(α) 0 │ = | x' y' z' |
│ 0 0 1 │
변환 수식은 다음과 같습니다.
x' = cos(α) · x - sin(α) · y
y' = sin(α) · x - cos(α) · y
α 0도인 경우 ID 행렬입니다. α 180도인 경우 변환 행렬은 다음과 같습니다.
| –1 0 0 | | 0 –1 0 | | 0 0 1 |
180도 회전은 개체를 가로 및 세로로 대칭 이동시키는 것과 같으며 배율 인수를 –1로 설정하여 수행됩니다.
이러한 모든 유형의 변환은 아핀 변환으로 분류됩니다. 아핀 변환에는 행렬의 세 번째 열이 포함되지 않습니다. 이 열은 기본값인 0, 0 및 1에서 다시 기본. 비아핀 변환 문서에서는 비아핀 변환에 대해 설명합니다.
행렬 곱
변환 매트릭스를 사용할 때의 한 가지 중요한 이점은 SkiaSharp 설명서에서 연결이라고 하는 행렬 곱셈을 통해 복합 변환을 얻을 수 있다는 것입니다. 대부분의 변환 관련 메서드는 SKCanvas "사전 연결" 또는 "사전 연결"을 참조합니다. 이는 행렬 곱셈이 정류되지 않기 때문에 중요한 곱셈 순서를 나타냅니다.
예를 들어 메서드에 대한 Translate 설명서에서는 "현재 행렬을 지정된 변환으로 미리 구성"하고 메서드에 대한 Scale 설명서는 "지정된 배율로 현재 행렬을 미리 구성합니다"라고 말합니다.
즉, 메서드 호출에 의해 지정된 변환은 승수(왼쪽 피연산자)이고 현재 변환 행렬은 곱셈(오른쪽 피연산자)입니다.
다음에 다음Scale이 Translate 호출되는 경우를 가정해 보겠습니다.
canvas.Translate(tx, ty);
canvas.Scale(sx, sy);
변환은 Scale 복합 변환 매트릭스의 Translate 변환을 곱합니다.
| sx 0 0 | | 1 0 0 | | sx 0 0 | | 0 sy 0 | × | 0 1 0 | = | 0 sy 0 | | 0 0 1 | | tx ty 1 | | tx ty 1 |
Scale 는 다음과 같이 이전에 Translate 호출할 수 있습니다.
canvas.Scale(sx, sy);
canvas.Translate(tx, ty);
이 경우 곱셈 순서가 반전되고 배율 인수가 변환 요소에 효과적으로 적용됩니다.
| 1 0 0 | | sx 0 0 | | sx 0 0 | | 0 1 0 | × | 0 sy 0 | = | 0 sy 0 | | tx ty 1 | | 0 0 1 | | tx·sx ty·sy 1 |
피벗 지점이 Scale 있는 메서드는 다음과 같습니다.
canvas.Scale(sx, sy, px, py);
이는 다음과 같은 변환 및 크기 조정 호출과 동일합니다.
canvas.Translate(px, py);
canvas.Scale(sx, sy);
canvas.Translate(–px, –py);
세 가지 변환 행렬은 메서드가 코드에 표시되는 방식과 역순으로 곱합니다.
| 1 0 0 | | sx 0 0 | | 1 0 0 | | sx 0 0 | | 0 1 0 | × | 0 sy 0 | × | 0 1 0 | = | 0 sy 0 | | –px –py 1 | | 0 0 1 | | px py 1 | | px–px·sx py–py·sy 1 |
SKMatrix 구조체
이 구조체는 SKMatrix 변환 행렬의 9개 셀에 해당하는 형식 float 의 읽기/쓰기 속성을 9개 정의합니다.
│ ScaleX SkewY Persp0 │ │ SkewX ScaleY Persp1 │ │ TransX TransY Persp2 │
SKMatrix는 형식의 float[]이름을 지정 Values 하는 속성도 정의합니다. 이 속성을 사용 하 고, , SkewX, ScaleYPersp1TransXSkewYTransYPersp0및 Persp2순서ScaleX로 한 샷에서 9 개의 값을 설정 하거나 가져올 수 있습니다.
, 및 셀은 비아핀 변환 문서에서 설명합니다.Persp2Persp1Persp0 이러한 셀의 기본값이 0, 0 및 1이면 변환에 다음과 같은 좌표점이 곱됩니다.
│ ScaleX SkewY 0 │
| x y 1 | × │ SkewX ScaleY 0 │ = | x' y' z' |
│ TransX TransY 1 │
x' = ScaleX · x + SkewX · y + TransX
y' = SkewX · x + ScaleY · y + TransY
z' = 1
이것은 완전한 2차원 아핀 변환입니다. 아핀 변환은 병렬 선을 유지합니다. 즉, 사각형이 병렬 프로그래밍 이외의 다른 항목으로 변환되지 않습니다.
이 구조체는 SKMatrix 값을 만드는 SKMatrix 여러 정적 메서드를 정의합니다. 이러한 모든 반환 SKMatrix 값은 다음과 같습니다.
MakeTranslationMakeScaleMakeScale피벗 지점이 있는 경우MakeRotation라디안 단위 각도MakeRotation피벗 점이 있는 라디안 단위 각도MakeRotationDegreesMakeRotationDegrees피벗 지점이 있는 경우MakeSkew
SKMatrix 또한 두 행렬을 연결하여 곱하는 여러 정적 메서드를 정의합니다. 이러한 메서드는 이름이 지정ConcatPostConcat되고 PreConcat각 메서드에는 두 가지 버전이 있습니다. 이러한 메서드에는 반환 값이 없습니다. 대신 인수를 통해 ref 기존 SKMatrix 값을 참조합니다. 다음 예제 A에서 , B및 R ("result"의 경우)는 모두 SKMatrix 값입니다.
두 Concat 메서드는 다음과 같이 호출됩니다.
SKMatrix.Concat(ref R, A, B);
SKMatrix.Concat(ref R, ref A, ref B);
다음 곱셈을 수행합니다.
R = B × A
다른 메서드에는 두 개의 매개 변수만 있습니다. 첫 번째 매개 변수가 수정되고 메서드 호출에서 반환될 때 두 행렬의 곱이 포함됩니다. 두 PostConcat 메서드는 다음과 같이 호출됩니다.
SKMatrix.PostConcat(ref A, B);
SKMatrix.PostConcat(ref A, ref B);
이러한 호출은 다음 작업을 수행합니다.
A = A × B
두 PreConcat 메서드는 비슷합니다.
SKMatrix.PreConcat(ref A, B);
SKMatrix.PreConcat(ref A, ref B);
이러한 호출은 다음 작업을 수행합니다.
A = B × A
모든 ref 인수가 있는 이러한 메서드 버전은 기본 구현을 호출하는 데 약간 더 효율적이지만 코드를 읽고 인수가 있는 ref 항목이 메서드에 의해 수정된 것으로 가정하면 혼동될 수 있습니다. 또한 메서드 중 Make 하나의 결과인 인수를 전달하는 것이 편리한 경우가 많습니다. 예를 들면 다음과 같습니다.
SKMatrix result;
SKMatrix.Concat(result, SKMatrix.MakeTranslation(100, 100),
SKMatrix.MakeScale(3, 3));
그러면 다음 행렬이 만들어집니다.
│ 3 0 0 │ │ 0 3 0 │ │ 100 100 1 │
변환 변환을 곱한 크기 조정 변환입니다. 이 특정 경우 구조체는 SKMatrix 다음과 같은 SetScaleTranslate메서드를 사용하여 바로 가기를 제공합니다.
SKMatrix R = new SKMatrix();
R.SetScaleTranslate(3, 3, 100, 100);
생성자를 사용하는 SKMatrix 것이 안전한 몇 번 중 하나입니다. 메서드는 SetScaleTranslate 행렬의 9개 셀을 모두 설정합니다. 또한 정적 Rotate 및 RotateDegrees 메서드와 SKMatrix 함께 생성자를 사용하는 것이 안전합니다.
SKMatrix R = new SKMatrix();
SKMatrix.Rotate(ref R, radians);
SKMatrix.Rotate(ref R, radians, px, py);
SKMatrix.RotateDegrees(ref R, degrees);
SKMatrix.RotateDegrees(ref R, degrees, px, py);
이러한 메서드는 회전 변환을 기존 변환에 연결하지 않습니다. 메서드는 행렬의 모든 셀을 설정합니다. 값을 인스턴스화하지 않는다는 점을 제외하고 함수와 메서드가 SKMatrix 기능적으로 동일합니다.MakeRotationMakeRotationDegrees
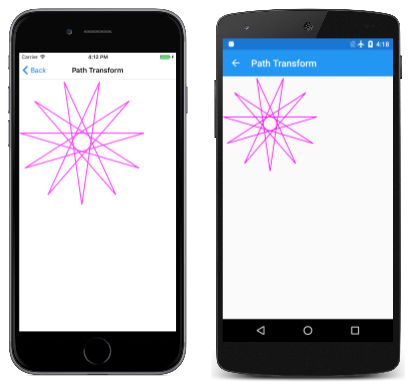
SKPath 표시하려는 개체가 있지만 방향이 다소 다르거나 중심점이 다른 것을 선호한다고 가정합니다. 인수를 사용하여 메서드를 호출하여 해당 경로의 SKPathSKMatrix 모든 좌표를 수정할 Transform 수 있습니다. 경로 변환 페이지에서 이 작업을 수행하는 방법을 보여 줍니다. 클래스는 PathTransform 필드의 HendecagramPath 개체를 참조하지만 해당 생성자를 사용하여 해당 경로에 변환을 적용합니다.
public class PathTransformPage : ContentPage
{
SKPath transformedPath = HendecagramArrayPage.HendecagramPath;
public PathTransformPage()
{
Title = "Path Transform";
SKCanvasView canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
SKMatrix matrix = SKMatrix.MakeScale(3, 3);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeRotationDegrees(360f / 22));
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(300, 300));
transformedPath.Transform(matrix);
}
...
}
개체의 HendecagramPath 중심은 (0, 0)이고 별의 11점은 해당 중심에서 바깥쪽으로 모든 방향으로 100단위까지 확장됩니다. 즉, 경로에는 양수 좌표와 음수 좌표가 모두 있습니다. 경로 변환 페이지에서는 별표가 세 배나 크고 모든 양수 좌표로 작업하는 것을 선호합니다. 또한 별의 한 지점이 똑바로 가리키기를 원하지 않습니다. 대신 별의 한 지점이 똑바로 가리키기를 원합니다. 별은 11점을 가지고 있기 때문에 둘 다 가질 수 없습니다.) 이를 위해서는 별을 22도로 나눈 360도 회전해야 합니다.
생성자는 다음 패턴이 있는 메서드를 사용하여 PostConcat 세 개의 개별 변환에서 개체를 빌드 SKMatrix 합니다. 여기서 A, B 및 C는 다음의 SKMatrix인스턴스입니다.
SKMatrix matrix = A;
SKMatrix.PostConcat(ref A, B);
SKMatrix.PostConcat(ref A, C);
일련의 연속 곱셈이므로 결과는 다음과 같습니다.
A × B × C
연속 곱셈은 각 변환이 수행하는 작업을 이해하는 데 도움이 됩니다. 배율 변환은 경로 좌표의 크기를 3인수로 늘리므로 좌표 범위는 –300에서 300까지입니다. 회전 변환은 별을 원점 주위로 회전합니다. 변환 변환은 오른쪽과 아래로 300픽셀씩 이동하므로 모든 좌표가 양수가 됩니다.
동일한 행렬을 생성하는 다른 시퀀스가 있습니다. 또 다른 방법은 다음과 같습니다.
SKMatrix matrix = SKMatrix.MakeRotationDegrees(360f / 22);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(100, 100));
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(3, 3));
이렇게 하면 경로가 먼저 중심을 중심으로 회전한 다음 100픽셀을 오른쪽 및 아래쪽으로 변환하므로 모든 좌표가 양수입니다. 별은 점 (0, 0)인 새로운 왼쪽 위 모서리에 비해 크기가 증가합니다.
PaintSurface 처리기는 이 경로를 간단히 렌더링할 수 있습니다.
public class PathTransformPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Magenta;
paint.StrokeWidth = 5;
canvas.DrawPath(transformedPath, paint);
}
}
}
캔버스의 왼쪽 위 모서리에 표시됩니다.
이 프로그램의 생성자는 다음 호출을 사용하여 경로에 행렬을 적용합니다.
transformedPath.Transform(matrix);
경로는 이 행렬을 속성으로 유지하지 않습니다. 대신 경로의 모든 좌표에 변환을 적용합니다. 다시 호출되면 Transform 변환이 다시 적용되고, 다시 돌아갈 수 있는 유일한 방법은 변환을 실행 취소하는 다른 행렬을 적용하는 것입니다. 다행히 구조체는 SKMatrix 지정된 행렬을 TryInvert 반대로 하는 행렬을 가져오는 메서드를 정의합니다.
SKMatrix inverse;
bool success = matrix.TryInverse(out inverse);
이 메서드는 모든 행렬을 반전할 수 없지만 반전할 수 없는 행렬이 그래픽 변환에 사용될 가능성이 없으므로 호출 TryInverse 됩니다.
또한 행렬 변환 SKPoint 을 값, 점 배열, SKRect또는 프로그램 내의 단일 숫자에 적용할 수도 있습니다. 구조체는 SKMatrix 다음과 같이 단어 Map로 시작하는 메서드 컬렉션을 사용하여 이러한 작업을 지원합니다.
SKPoint transformedPoint = matrix.MapPoint(point);
SKPoint transformedPoint = matrix.MapPoint(x, y);
SKPoint[] transformedPoints = matrix.MapPoints(pointArray);
float transformedValue = matrix.MapRadius(floatValue);
SKRect transformedRect = matrix.MapRect(rect);
마지막 메서드를 사용하는 경우 구조체가 SKRect 회전된 사각형을 나타낼 수 없습니다. 이 메서드는 변환 및 크기 조정을 나타내는 값에만 적합 SKMatrix 합니다.
대화형 실험
아핀 변환에 대한 느낌을 얻는 한 가지 방법은 대화형으로 비트맵의 세 모서리를 화면 주위로 이동하고 어떤 변환 결과를 확인하는 것입니다. 이것은 쇼 아핀 매트릭스 페이지 뒤에 아이디어입니다 . 이 페이지에는 다른 데모에도 사용되는 두 개의 다른 클래스가 필요합니다.
클래스는 TouchPoint 화면 주위에 끌 수 있는 반투명 원을 표시합니다. TouchPoint에는 부모 SKCanvasView 인 SKCanvasView 요소 또는 연결된 요소가 있어야 합니다TouchEffect. Capture 속성을 true로 설정합니다. TouchAction 이벤트 처리기에서 프로그램은 각 TouchPoint 인스턴스에 대해 메서드 TouchPoint 를 ProcessTouchEvent 호출해야 합니다. 이 메서드는 터치 이벤트로 인해 터치 포인트가 이동했는지를 반환 true 합니다. PaintSurface 또한 처리기는 각 TouchPoint 인스턴스에서 메서드를 Paint 호출하여 개체에 SKCanvas 전달해야 합니다.
TouchPoint 는 SkiaSharp 시각적 개체를 별도의 클래스에 캡슐화할 수 있는 일반적인 방법을 보여 줍니다. 클래스는 시각적 개체의 특성을 지정하기 위한 속성을 정의할 수 있으며 인수를 사용하여 명명된 Paint 메서드가 SKCanvas 렌더링할 수 있습니다.
개체 Center 의 TouchPoint 위치를 나타내는 속성입니다. 이 속성을 설정하여 위치를 초기화할 수 있습니다. 사용자가 캔버스 주위에 원을 끌면 속성이 변경됩니다.
아핀 행렬 표시 페이지에는 클래스도 필요합니다MatrixDisplay. 이 클래스는 개체의 셀을 SKMatrix 표시합니다. 렌더링된 행렬의 차원을 가져오고 Paint 표시하는 두 가지 공용 메서드 Measure 가 있습니다. 클래스에는 MatrixPaint 다른 글꼴 크기 또는 색으로 바꿀 수 있는 형식 SKPaint 의 속성이 포함되어 있습니다.
ShowAffineMatrixPage.xaml 파일은 인스턴스화 SKCanvasView 하고 TouchEffect. ShowAffineMatrixPage.xaml.cs 코드 숨김 파일은 세 개의 TouchPoint 개체를 만든 다음 포함된 리소스에서 로드하는 비트맵의 세 모서리에 해당하는 위치로 설정합니다.
public partial class ShowAffineMatrixPage : ContentPage
{
SKMatrix matrix;
SKBitmap bitmap;
SKSize bitmapSize;
TouchPoint[] touchPoints = new TouchPoint[3];
MatrixDisplay matrixDisplay = new MatrixDisplay();
public ShowAffineMatrixPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
touchPoints[0] = new TouchPoint(100, 100); // upper-left corner
touchPoints[1] = new TouchPoint(bitmap.Width + 100, 100); // upper-right corner
touchPoints[2] = new TouchPoint(100, bitmap.Height + 100); // lower-left corner
bitmapSize = new SKSize(bitmap.Width, bitmap.Height);
matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
touchPoints[1].Center,
touchPoints[2].Center);
}
...
}
아핀 행렬은 3점으로 고유하게 정의됩니다. 세 TouchPoint 개체는 비트맵의 왼쪽 위, 오른쪽 위 및 왼쪽 아래 모서리에 해당합니다. 아핀 행렬은 직사각형을 병렬로 변환할 수 있기 때문에 네 번째 점은 다른 세 가지에 의해 암시됩니다. 생성자는 이 세 가지 지점에서 개체의 셀을 계산하는 호출 ComputeMatrix로 SKMatrix 끝납니다.
TouchAction 처리기는 각 TouchPoint메서드를 ProcessTouchEvent 호출합니다. 값은 scale 좌표에서 Xamarin.Forms 픽셀로 변환됩니다.
public partial class ShowAffineMatrixPage : ContentPage
{
...
void OnTouchEffectAction(object sender, TouchActionEventArgs args)
{
bool touchPointMoved = false;
foreach (TouchPoint touchPoint in touchPoints)
{
float scale = canvasView.CanvasSize.Width / (float)canvasView.Width;
SKPoint point = new SKPoint(scale * (float)args.Location.X,
scale * (float)args.Location.Y);
touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
}
if (touchPointMoved)
{
matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
touchPoints[1].Center,
touchPoints[2].Center);
canvasView.InvalidateSurface();
}
}
...
}
TouchPoint 이동한 경우 메서드가 다시 호출 ComputeMatrix 되고 표면이 무효화됩니다.
메서드는 ComputeMatrix 이러한 세 가지 점에 내포된 행렬을 결정합니다. 이 행렬은 A 1픽셀 정사각형 사각형을 3포인트에 따라 병렬 변환으로 변환하는 반면, 비트맵이라는 S 배율 변환은 비트맵을 1픽셀 정사각형 사각형으로 확장합니다. 복합 행렬은 S 다음과 같이 × A.
public partial class ShowAffineMatrixPage : ContentPage
{
...
static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL)
{
// Scale transform
SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);
// Affine transform
SKMatrix A = new SKMatrix
{
ScaleX = ptUR.X - ptUL.X,
SkewY = ptUR.Y - ptUL.Y,
SkewX = ptLL.X - ptUL.X,
ScaleY = ptLL.Y - ptUL.Y,
TransX = ptUL.X,
TransY = ptUL.Y,
Persp2 = 1
};
SKMatrix result = SKMatrix.MakeIdentity();
SKMatrix.Concat(ref result, A, S);
return result;
}
...
}
마지막으로, 메서드는 PaintSurface 해당 행렬을 기반으로 비트맵을 렌더링하고, 화면 아래쪽에 행렬을 표시하고, 비트맵의 세 모서리에 터치 포인트를 렌더링합니다.
public partial class ShowAffineMatrixPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Display the bitmap using the matrix
canvas.Save();
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, 0, 0);
canvas.Restore();
// Display the matrix in the lower-right corner
SKSize matrixSize = matrixDisplay.Measure(matrix);
matrixDisplay.Paint(canvas, matrix,
new SKPoint(info.Width - matrixSize.Width,
info.Height - matrixSize.Height));
// Display the touchpoints
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
}
아래 iOS 화면에는 페이지가 처음 로드될 때 비트맵이 표시되고, 다른 두 화면은 조작 후에 해당 비트맵을 표시합니다.
터치 포인트가 비트맵의 모서리를 끄는 것처럼 보이지만 이는 환상일 뿐입니다. 터치 포인트에서 계산된 행렬은 비트맵을 변환하여 모서리가 터치 포인트와 일치하도록 합니다.
사용자가 모서리를 끄는 것이 아니라 개체에서 한두 손가락을 직접 사용하여 끌어서, 꼬집고, 회전하는 방식으로 비트맵을 이동하고, 크기를 조정하고, 회전하는 것이 더 자연스러워집니다. 이 내용은 다음 문서 터치 조작에서 다룹니다.
3-by-3 행렬의 이유
2차원 그래픽 시스템에는 2x2 변환 매트릭스만 필요할 수 있습니다.
│ ScaleX SkewY │
| x y | × │ │ = | x' y' |
│ SkewX ScaleY │
크기 조정, 회전 및 기울이기에는 작동하지만 변환인 가장 기본적인 변환은 수행할 수 없습니다.
문제는 2 x 2 행렬이 2 차원의 선형 변환을 나타낸다는 것입니다. 선형 변환은 몇 가지 기본 산술 연산을 유지하지만 선형 변환이 점(0, 0)을 변경하지 않는다는 의미 중 하나입니다. 선형 변환은 번역을 불가능하게 만듭니다.
3차원에서 선형 변환 행렬은 다음과 같습니다.
│ ScaleX SkewYX SkewZX │
| x y z | × │ SkewXY ScaleY SkewZY │ = | x' y' z' |
│ SkewXZ SkewYZ ScaleZ │
레이블이 지정된 SkewXY 셀은 값이 Y 값을 기준으로 X 좌표를 기울이는 것을 의미합니다. 셀 SkewXZ 은 값이 Z 값을 기준으로 X 좌표를 왜곡하고 값이 다른 Skew 셀에 대해 비슷하게 기울어진다는 것을 의미합니다.
다음 3D 변환 매트릭스를 2차원 평면 SkewZX 으로, 0으로 SkewZY , 1로 제한할 수 있습니다 ScaleZ .
│ ScaleX SkewYX 0 │
| x y z | × │ SkewXY ScaleY 0 │ = | x' y' z' |
│ SkewXZ SkewYZ 1 │
2차원 그래픽이 Z가 1인 3D 공간의 평면에 완전히 그려지면 변환 곱셈은 다음과 같습니다.
│ ScaleX SkewYX 0 │
| x y 1 | × │ SkewXY ScaleY 0 │ = | x' y' 1 |
│ SkewXZ SkewYZ 1 │
모든 항목은 Z가 1인 2차원 평면에 유지되지만 SkewXZ 셀과 SkewYZ 셀은 효과적으로 2차원 변환 요소가 됩니다.
이것이 3차원 선형 변환이 2차원 비선형 변환 역할을 하는 방법입니다. (비유로, 3D 그래픽의 변환은 4x4 행렬을 기반으로 합니다.)
SkiaSharp의 구조체는 SKMatrix 세 번째 행에 대한 속성을 정의합니다.
│ ScaleX SkewY Persp0 │
| x y 1 | × │ SkewX ScaleY Persp1 │ = | x' y' z` |
│ TransX TransY Persp2 │
0이 아닌 값 Persp0 은 Persp1 Z가 1인 2차원 평면에서 개체를 이동하는 변환으로 이어집니다. 이러한 개체를 해당 평면으로 다시 이동하면 발생하는 작업은 비아핀 변환에 대한 문서에서 다룹니다.